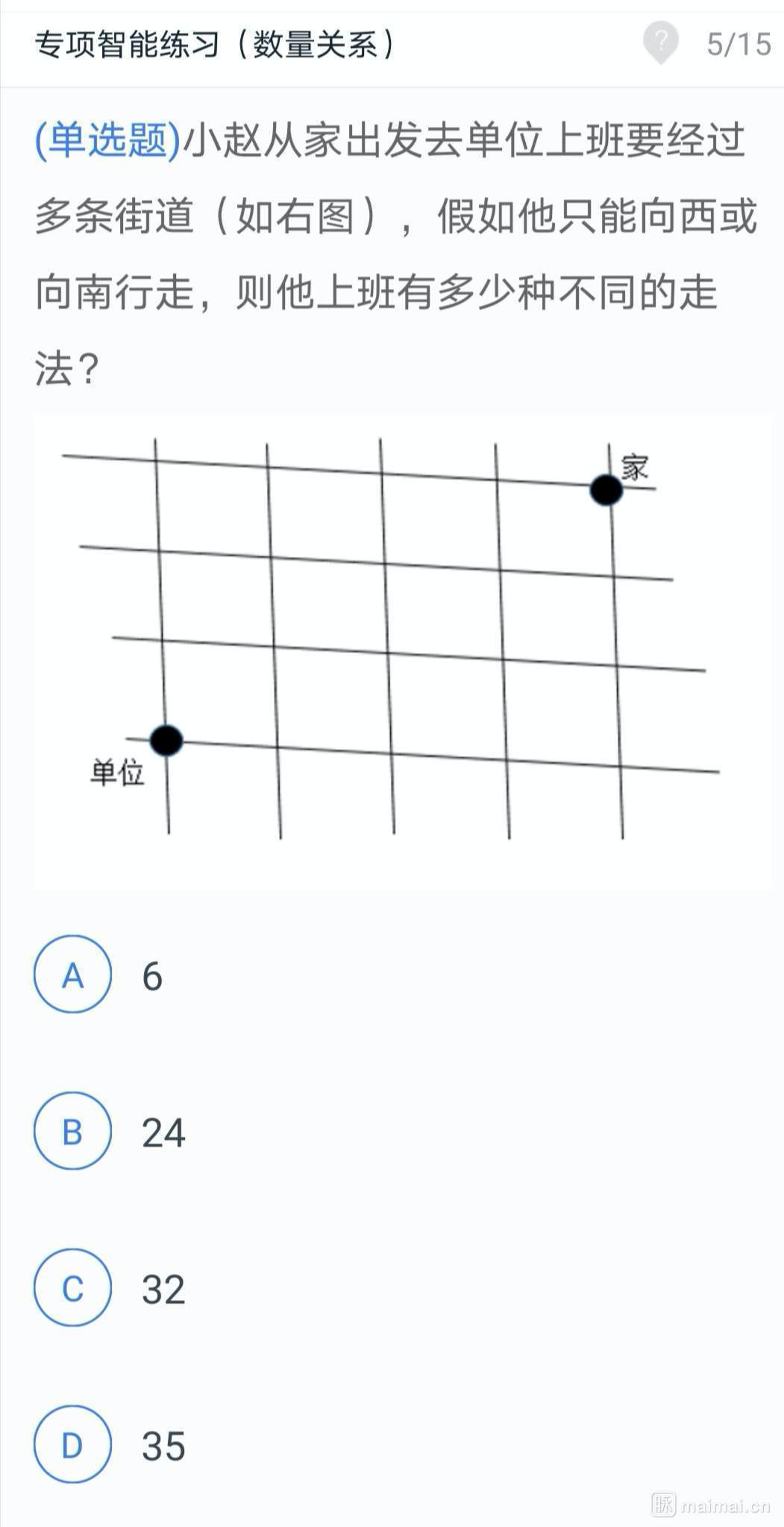
今天在脉脉上看到有人发了一道公务员的考试题,题目如下:
这道题可以用数学方法来做,但我离开学校很多年了,想不出数学的解法。不过看到题目的一瞬间,我就想到了可以使用动态规划来解决这个问题。
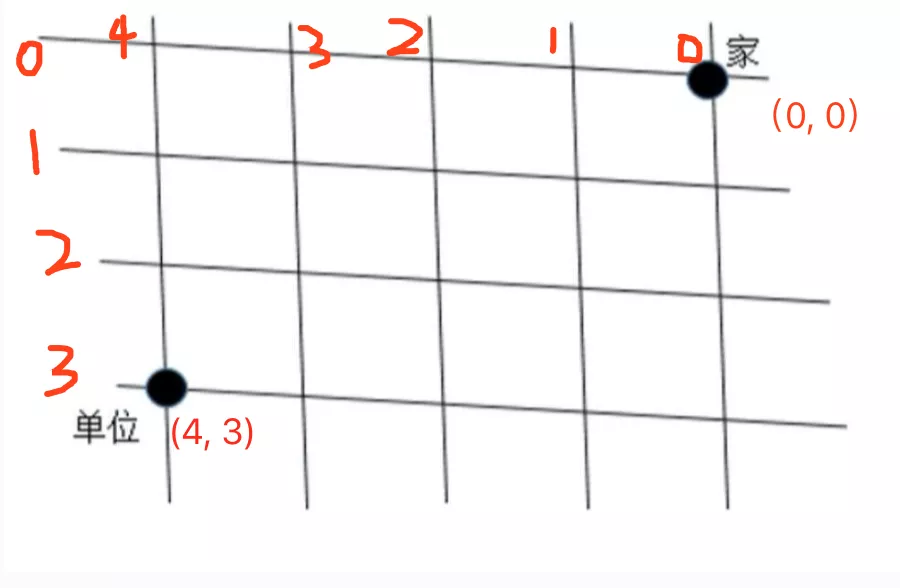
我们把“家”的位置标记为(0, 0),把单位的位置标记为(4, 3),如下图所示:
动态规划的一个典型解法,就是想问题的时候,倒着想。假设现在我已经在单位(4, 3)了。我上一步是在哪里?要到(4, 3),只有两种方法,从(3, 3)到(4, 3)或者从(4, 2)到(4, 3)。现在问题的规模缩小了,变成了两个小问题,一个是从家(0, 0)到(4, 2)有多少种走法,另一个是从家(0, 0)到(3, 3)有多少种走法。
到这里,我们看出来这实际上是一个递归问题,也就是fn(x, y) = f(x - 1, y) + f(x, y - 1)。
不过,这里要考虑另一个问题,就是当我们在fn(x, 0)或者fn(0, y)的时候。如果 x > 1,那么此时只有一种走法,就是从(x-1, 0)到 (x, 0)。如果x == 1,那么此时只能是从(0, 0)到(1, 0)。同理,对于(0, y)也是一样,如果y > 1,那么只能从(0, y - 1)到(0, y)。如果y == 1,那么只能是从(0, 0)到(0, 1)。
于是,根据这个思路,我们可以写出如下的代码:
- def find_walk_num(x, y):
- if y == 0:
- if x == 1:
- return 1
- return find_walk_num(x - 1, 0)
- if x == 0:
- if y == 1:
- return 1
- return find_walk_num(0, y - 1)
- return find_walk_num(x - 1, y) + find_walk_num(x, y - 1)
- result = find_walk_num(4, 3)
- print(f'从(0, 0)到(4, 3)的走法一共有:{result}种')
运行效果如下图所示:
所以这道题的答案就是 D,一共有35种走法。