深入了解离群值检测以及如何在Python中实现3个简单,直观且功能强大的离群值检测算法
> Photo By Scott.T on Flickr
我确定您遇到以下几种情况:
- 您的模型表现不理想。
- 您不禁会注意到有些地方似乎与其他地方有很大的不同。
恭喜,因为您的数据中可能包含异常值!
什么是离群值?
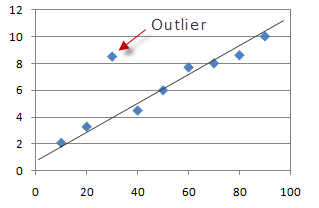
> Photo can be found in StackExchange
在统计中,离群点是与其他观察值有显着差异的数据点。 从上图可以清楚地看到,尽管大多数点都位于线性超平面内或周围,但可以看到单个点与其余超散点不同。 这是一个离群值。
例如,查看下面的列表:
- [1,35,20,32,40,46,45,4500]
在这里,很容易看出1和4500在数据集中是异常值。
为什么我的数据中有异常值?
通常,异常可能发生在以下情况之一:
- 有时可能由于测量错误而偶然发生。
- 有时它们可能会出现在数据中,因为在没有异常值的情况下,数据很少是100%干净的。
为什么离群值有问题?
原因如下:
线性模型
假设您有一些数据,并且想使用线性回归从中预测房价。 可能的假设如下所示:
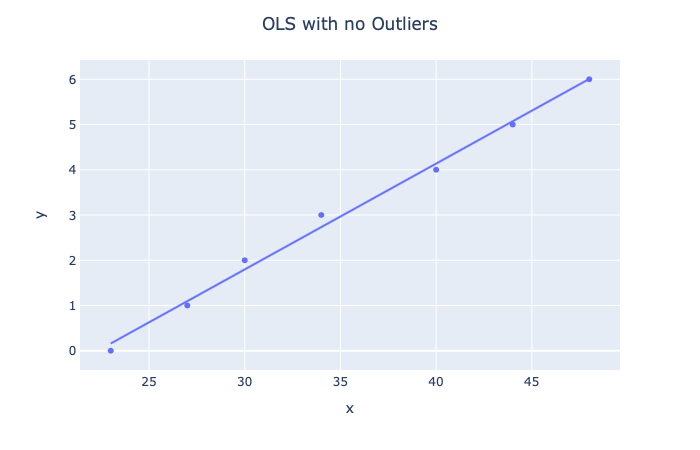
> Source: http> Photo By Authors://arxiv.org/pdf/1811.06965.pdf
在这种情况下,我们实际上将数据拟合得太好(过度拟合)。 但是,请注意所有点的位置大致在同一范围内。
现在,让我们看看添加异常值时会发生什么。
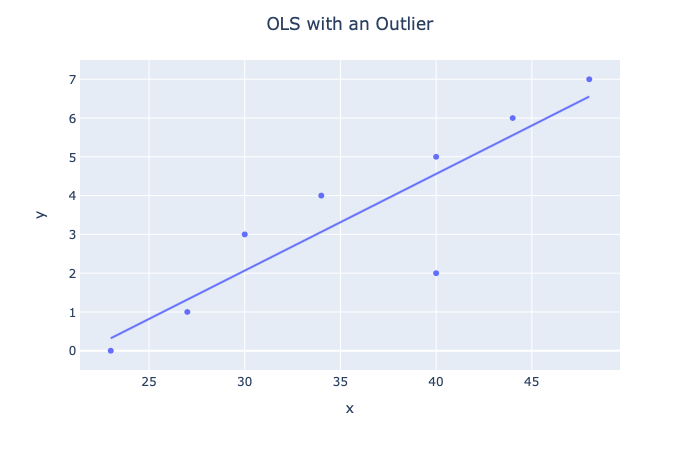
> Photo By Author
显然,我们看到了假设的变化,因此,如果没有异常值,推断将变得更加糟糕。 线性模型包括:
- 感知器
- 线性+ Logistic回归
- 神经网络
- 知识网络
数据插补
常见的情况是缺少数据,可以采用以下两种方法之一:
- 删除缺少行的实例
- 使用统计方法估算数据
如果我们选择第二种方法,我们可能会得出有问题的推论,因为离群值会极大地改变统计方法的值。 例如,回到没有异常值的虚构数据:
- # Data with no outliers
- np.array([35,20,32,40,46,45]).mean() = 36.333333333333336
- # Data with 2 outliers
- np.array([1,35,20,32,40,46,45,4500]).mean() = 589.875
显然,这种类比是极端的,但是想法仍然相同。 我们数据中的异常值通常是一个问题,因为异常值会在统计分析和建模中引起严重的问题。 但是,在本文中,我们将探讨几种检测和打击它们的方法。
解决方案1:DBSCAN
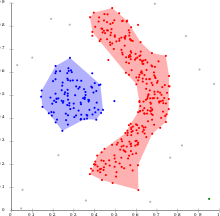
> Photo By Wikipedia
像KMeans一样,带有噪声(或更简单地说是DBSCAN)的应用程序的基于密度的空间聚类实际上是一种无监督的聚类算法。 但是,其用途之一还在于能够检测数据中的异常值。
DBSCAN之所以受欢迎,是因为它可以找到非线性可分离的簇,而KMeans和高斯混合无法做到这一点。 当簇足够密集且被低密度区域隔开时,它会很好地工作。
DBSCAN工作原理的高级概述
该算法将群集定义为高密度的连续区域。 该算法非常简单:
- 对于每个实例,它计算在距它的小距离ε(ε)内有多少个实例。 该区域称为实例的ε社区。
- 如果该实例在其ε邻域中有多个min_samples个实例,则将其视为核心实例。 这意味着实例位于高密度区域(内部有很多实例的区域)。
- 核心实例的ε邻域内的所有实例都分配给同一群集。 这可能包括其他核心实例,因此相邻核心实例的单个长序列形成单个群集。
- 不是核心实例或不在任何核心实例的ε邻居中的任何实例都是异常值。
DBSCAN实战
借助Scikit-Learn直观的API,DBSCAN算法非常易于使用。 让我们看一个实际的算法示例:
- from sklearn.cluster import DBSCAN
- from sklearn.datasets import make_moons
- X, y = make_moons(n_samples=1000, noise=0.05)
- dbscan = DBSCAN(eps=0.2, min_samples=5)
- dbscan.fit(X)
在这里,我们将实例化一个具有ε邻域长度为0.05的DBSCAN,并将5设为实例被视为核心实例所需的最小样本数
请记住,我们不传递标签,因为它是无监督的算法。 我们可以使用以下命令查看标签,即算法生成的标签:
- dbscan.labels_
- OUT:array([ 0, 2, -1, -1, 1, 0, 0, 0, ..., 3, 2, 3, 3, 4, 2, 6, 3])
请注意一些标签的值如何等于-1:这些是离群值。
DBSCAN没有预测方法,只有fit_predict方法,这意味着它无法对新实例进行聚类。 相反,我们可以使用其他分类器进行训练和预测。 在此示例中,我们使用KNN:
- from sklearn.neighbors import KNeighborsClassifier
- knn = KNeighborsClassifier(n_neighbors=50)
- knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])
- X_new = np.array([[-0.5, 0], [0, 0.5], [1, -0.1], [2, 1]])
- knn.predict(X_new)
- OUT:array([1, 0, 1, 0])
在这里,我们将KNN分类器适合核心样本及其各自的邻居。
但是,我们遇到了一个问题。 我们提供的KNN数据没有任何异常值。 这是有问题的,因为它将迫使KNN为新实例选择群集,即使新实例确实是异常值。
为了解决这个问题,我们利用了KNN分类器的kneighbors方法,该方法在给定一组实例的情况下,返回训练集的k个最近邻居的距离和索引。 然后,我们可以设置最大距离,如果实例超过该距离,我们会将其限定为离群值:
- y_dist, y_pred_idx = knn.kneighbors(X_new, n_neighbors=1)
- y_pred = dbscan.labels_[dbscan.core_sample_indices_][y_pred_idx]
- y_pred[y_dist > 0.2] = -1y_pred.ravel()
- OUT:array([-1, 0, 1, -1])
在这里,我们已经讨论并实现了用于异常检测的DBSCAN。 DBSCAN很棒,因为它速度快,只有两个超参数并且对异常值具有鲁棒性。
解决方案2:IsolationForest
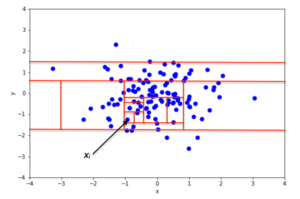
> Photo By Author
IsolationForest是一种集成学习异常检测算法,在检测高维数据集中的异常值时特别有用。 该算法基本上执行以下操作:
- 它创建了一个随机森林,其中决策树是随机增长的:在每个节点上,特征都是随机选择的,并且它选择一个随机阈值将数据集一分为二。
- 它会继续砍掉数据集,直到所有实例最终相互隔离。
- 异常通常与其他实例相距甚远,因此,平均而言(在所有决策树中),与正常实例相比,异常隔离的步骤更少。
行动中的森林
同样,借助Scikit-Learn直观的API,我们可以轻松实现IsolationForest类。 让我们看一个实际的算法示例:
- from sklearn.ensemble import IsolationForest
- from sklearn.metrics import mean_absolute_error
- import pandas as pd
我们还将导入mean_absolute_error来衡量我们的错误。 对于数据,我们将使用可从Jason Brownlee的GitHub获得的数据集:
- url='https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
- df = pd.read_csv(url, header=None)
- data = df.values
- # split into input and output elements
- X, y = data[:, :-1], data[:, -1]
在拟合隔离森林之前,让我们尝试在数据上拟合香草线性回归模型并获得MAE:
- from sklearn.linear_model import LinearRegression
- lr =LinearRegression()
- lr.fit(X,y)
- mean_absolute_error(lr.predict(X),y)
- OUT:3.2708628109003177
分数比较好。 现在,让我们看看隔离林是否可以通过消除异常来提高得分!
首先,我们将实例化IsolationForest:
- iso = IsolationForest(contamination='auto',random_state=42)
该算法中最重要的超参数可能是污染参数,该污染参数用于帮助估计数据集中的异常值。 这是介于0.0和0.5之间的值,默认情况下设置为0.1
但是,它本质上是随机的随机森林,因此随机森林的所有超参数也可以在算法中使用。
接下来,我们将数据拟合到算法中:
- y_pred = iso.fit_predict(X,y)
- mask = y_pred != -1
请注意,我们如何也过滤掉预测值= -1,就像在DBSCAN中一样,这些被认为是离群值。
现在,我们将使用异常值过滤后的数据重新分配X和Y:
- X,y = X[mask,:],y[mask]
现在,让我们尝试将线性回归模型拟合到数据中并测量MAE:
- lr.fit(X,y)
- mean_absolute_error(lr.predict(X),y)
- OUT:2.643367450077622
哇,成本大大降低了。 这清楚地展示了隔离林的力量。
解决方案3:Boxplots + Tuckey方法
虽然Boxplots是识别异常值的一种常见方法,但我确实发现,后者可能是识别异常值的最被低估的方法。 但是在我们进入" Tuckey方法"之前,让我们先谈一下Boxplots:
箱线图
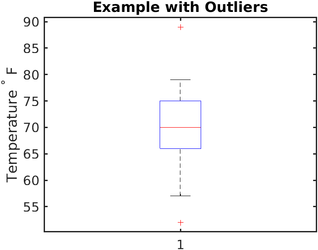
> Photo By Wikipedia
箱线图实质上提供了一种通过分位数显示数值数据的图形方式,这是一种非常简单但有效的可视化异常值的方式。
上下晶须显示了分布的边界,任何高于或低于此的值都被认为是异常值。 在上图中,高于〜80和低于〜62的任何值都被认为是异常值。
Boxplots如何工作
本质上,箱形图通过将数据集分为5部分来工作:
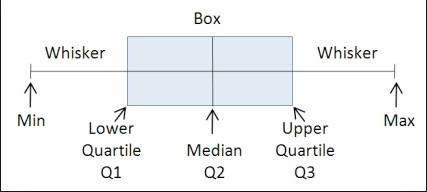
> Photo from StackOverflow
- 最小值:分布中的最低数据点,不包括任何异常值。
- 最大值:分布中的最高数据点,不包括任何异常值。
- 中位数(Q2 / 50%):数据集的中间值。
- 第一个四分位数(Q1 / 25个百分点):是数据集下半部分的中位数。
- 第三四分位数(Q3 /第75个百分位数):是数据集上半部分的中位数。
四分位间距(IQR)很重要,因为它定义了异常值。 本质上,它是以下内容:
- IQR = Q3 - Q1
- Q3: third quartile
- Q1: first quartile
在箱图中,测得的距离为1.5 * IQR,并包含数据集的较高观测点。 类似地,在数据集的较低观察点上测得的距离为1.5 * IQR。 这些距离之外的任何值都是异常值。 进一步来说:
- 如果观测点低于(Q1-1.5 * IQR)或箱线图下部晶须,则将其视为异常值。
- 同样,如果观测点高于(Q3 + 1.5 * IQR)或箱线图上晶须,则它们也被视为离群值。
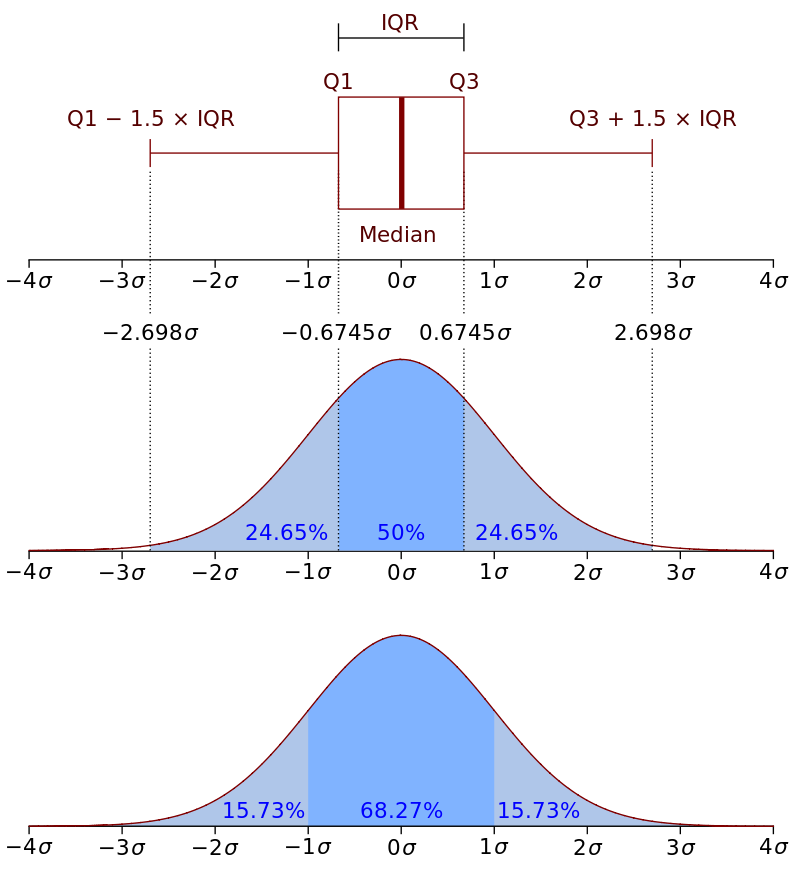
> Photo By Wikipedia
箱线图在行动
让我们看看如何在Python中使用Boxplots检测离群值!
- import matplotlib.pyplot as plt
- import seaborn as sns
- import numpy as np
- X = np.array([45,56,78,34,1,2,67,68,87,203,-200,-150])
- y = np.array([1,1,0,0,1,0,1,1,0,0,1,1])
让我们绘制数据的箱线图:
- sns.boxplot(X)
- plt.show()
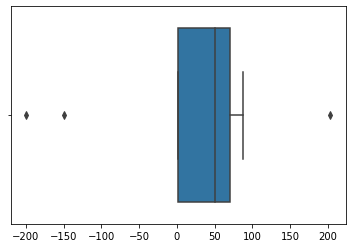
> Photo By Author
因此,根据箱线图,我们看到我们的数据中位数为50和3个离群值。 让我们摆脱这些要点:
- X = X[(X < 150) & (X > -50)]
- sns.boxplot(X)
- plt.show()
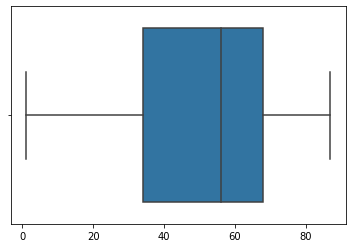
> Photo By Author
在这里,我基本上设置了一个阈值,以便将所有小于-50和大于150的点都排除在外。 结果 分布均匀!
Tukey方法离群值检测
曲棍球方法离群值检测实际上是箱形图的非可视方法; 除了没有可视化之外,方法是相同的。
我有时喜欢这种方法而不是箱线图的原因是因为有时看一下可视化并粗略估计应将阈值设置为什么,实际上并没有效果。
相反,我们可以编写一种算法,该算法实际上可以返回它定义为异常值的实例。
该实现的代码如下:
- import numpy as np
- from collections import Counter
- def detect_outliers(df, n, features):
- # list to store outlier indices
- outlier_indices = []
- # iterate over features(columns)
- for col in features:
- # Get the 1st quartile (25%)
- Q1 = np.percentile(df[col], 25)
- # Get the 3rd quartile (75%)
- Q3 = np.percentile(df[col], 75)
- # Get the Interquartile range (IQR)
- IQR = Q3 - Q1
- # Define our outlier step
- outlier_step = 1.5 * IQR
- # Determine a list of indices of outliers
- outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index
- # append outlier indices for column to the list of outlier indices
- outlier_indices.extend(outlier_list_col)
- # select observations containing more than 2 outliers
- outlier_indices = Counter(outlier_indices)
- multiple_outliers = list(k for k, v in outlier_indices.items() if v > n)
- return multiple_outliers
- # detect outliers from list of features
- list_of_features = ['x1', 'x2']
- # params dataset, number of outliers for rejection, list of features
- Outliers_to_drop = detect_outliers(dataset, 2, list_of_features)
基本上,此代码执行以下操作:
- 对于每个功能,它都会获得:
- 第一四分位数
- 第三四分位数
- IQR
2.接下来,它定义离群值步骤,就像在箱图中一样,为1.5 * IQR
3.通过以下方式检测异常值:
- 查看观察点是否
- 查看观察点是否为Q3 +离群步
4.然后检查选择的观察值具有k个异常值(在这种情况下,k = 2)
结论
总而言之,存在许多离群值检测算法,但是我们经历了3种最常见的算法:DBSCAN,IsolationForest和Boxplots。 我鼓励您:
- 在"泰坦尼克号"数据集上尝试这些方法。 哪一个最能检测到异常值?
- 寻找其他异常检测方法,看看它们的性能比最初尝试得更好还是更差。
我真的很感谢我的追随者,并希望不断写信并给予大家深思熟虑的食物。 但是,现在,我必须说再见;}