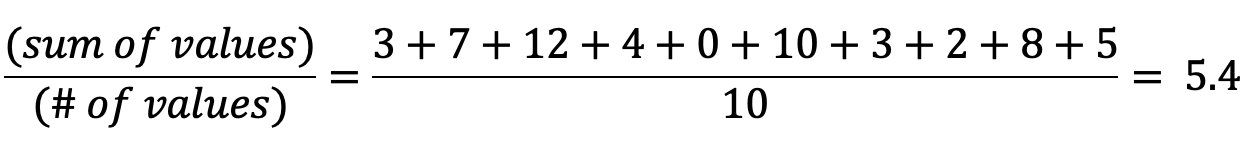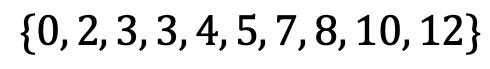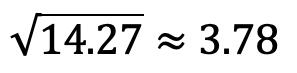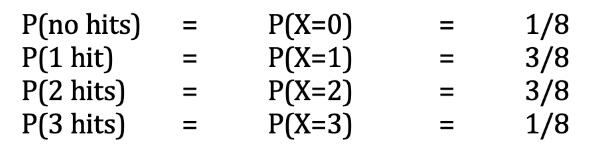统计和数据科学的重要支柱
任何数据科学家都可以从数据集中收集信息-任何优秀的数据科学家都将知道,扎实的统计基础可以收集有用和可靠的信息。 没有它,就不可能进行高质量的数据科学。
> Photo by Tachina Lee on Unsplash
但是统计是一个巨大的领域! 我从哪说起呢?
以下是每个数据科学家都应该知道的前五个统计概念:描述性统计,概率分布,降维,过采样和欠采样以及贝叶斯统计。
让我们从最简单的一个开始。
1. 描述性统计
您正坐在数据集的前面。 您如何对自己所拥有的东西有一个高层次的描述? 描述性统计就是答案。 您可能已经听说过其中的一些:平均值,中位数,众数,方差,标准差…
这些将快速识别您的数据集的关键特征,并在您执行任务时通知您的方法。 让我们来看看一些最常见的描述性统计数据。
意思
平均值(也称为"期望值"或"平均值")是值的总和除以值的数量。 采取以下示例集:
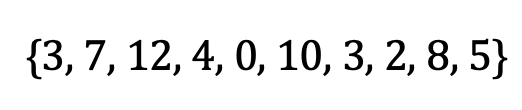
平均值计算如下:
中位数
以升序(或降序)列出您的值。 中位数是将数据分成两半的点。 如果有两个中间数字,则中位数是这些数字的平均值。 在我们的示例中:
中位数为4.5。
模式
模式是数据集中最频繁的值。 在我们的示例中,模式为3。
方差
方差衡量数据集相对于均值的分布。 要计算方差,请从每个值中减去平均值。 平方每个差异。 最后,计算这些结果数字的平均值。 在我们的示例中:
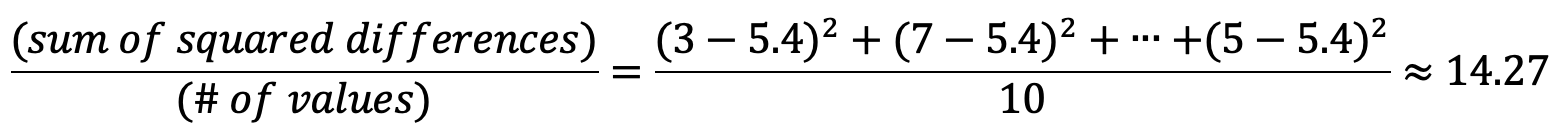
标准偏差
标准差用于衡量总体价差,并通过求出方差的平方根来计算。 在我们的示例中:
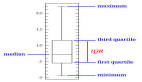
其他描述性统计数据包括偏度,峰度和四分位数。
2. 概率分布
概率分布是一种函数,它给出实验每个可能结果的出现概率。 如果您要绘制钟形曲线,那您就走对了。 乍一看,它显示了如何分散随机变量的值。 随机变量及其分布可以是离散的也可以是连续的。
离散的
约翰是一名棒球运动员,每次向他投球时,都有50%的随机击球机会。 让我们向约翰投三个球,看看他有多少次击球。 以下是所有可能结果的列表:

令X为我们的随机变量,即约翰在三音高实验中被击中的次数。 约翰获得n次点击的概率由P(X = n)表示。 因此,X可以为0、1、2或3。如果上述所有八个结果均具有相同的可能性,则我们有:
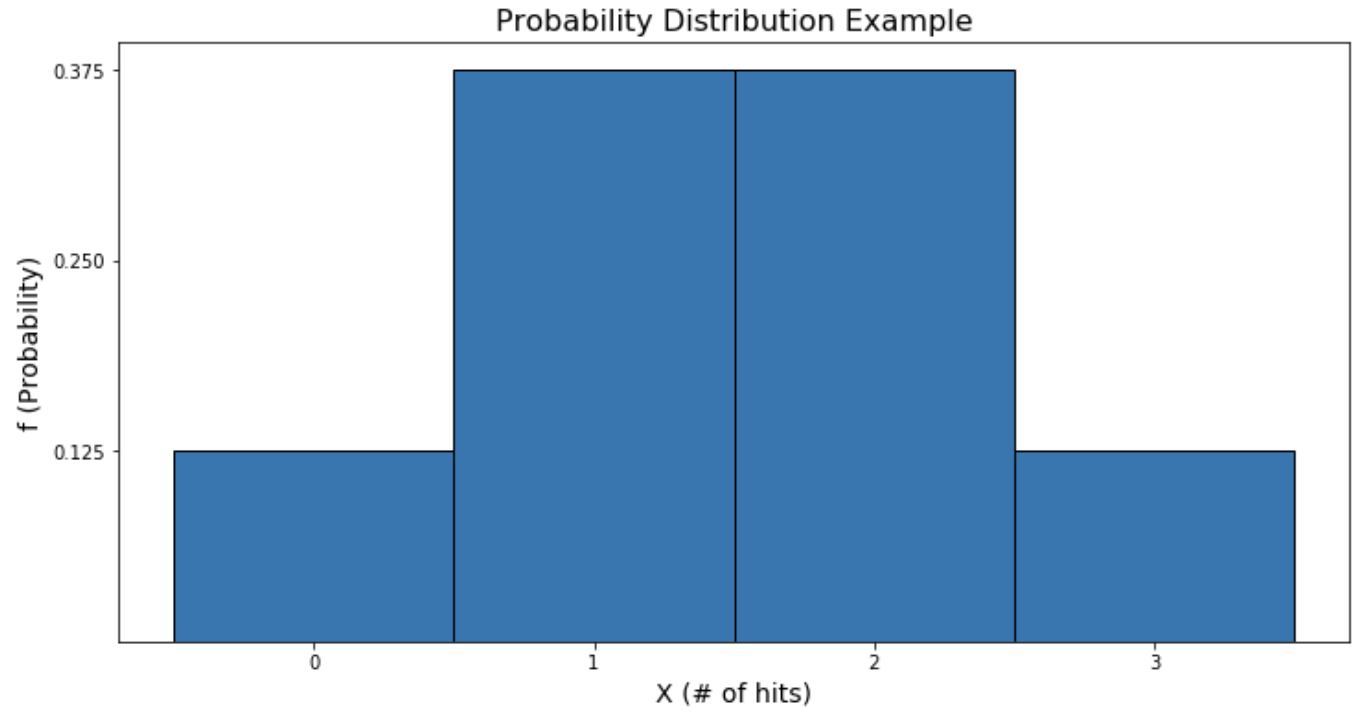
用f代替P,我们就有了概率函数! 让我们来画一下。
从图中可以看出,John获得1或2次命中比获得0或3次命中的可能性更大,因为对于那些X值,该图更高。常见的离散分布包括伯努利,二项式和 泊松
连续
连续情况自然而然地来自离散情况。 除了计算命中率外,我们的随机变量可能是棒球播出的时间。 我们可以将值设置为3.45秒或6.98457秒,而不仅仅是一秒,两秒或三秒。
我们正在谈论无限多种可能性。 连续变量的其他示例是高度,时间和温度。 常见的连续分布包括正态,指数和卡方。
3. 降维
如果输入变量太多或数据计算笨拙,则可以转向降维。 这是将高维数据投影到低维空间的过程,但是请务必注意不要丢失原始数据集的重要特征。
例如,假设您正在尝试确定哪些因素可以最好地预测您最喜欢的篮球队今晚能否赢得比赛。 您可能会收集数据,例如他们的获胜百分比,他们在踢球,在哪里踢球,他们的前锋是谁,他吃晚餐的时间以及教练穿什么颜色的鞋子。
您可能会怀疑其中某些功能比其他功能与获胜的相关性更高。 降维可以使我们放心地删除不会对预测做出有意义贡献的信息,同时保留具有最大预测价值的特征。
主成分分析(PCA)是一种流行的方法,它通过夸大称为主成分的要素的新组合的方差来工作。 这些新组合是原始数据点到新空间(仍是相同维度)的投影,其中会显示变化。
通常的想法是,在这些新组件中,变化最小的组件可以最安全地删除。 删除单个组件将使原始尺寸减小一倍,删除两个组件将使尺寸减小两个,依此类推。
4. 欠采样和过采样
收集的一组观测值称为"样本",而收集观测值的方式称为"采样"。 在需要平等代表少数派和多数派的分类情况下,欠采样或过采样可能会有用。 对多数类别进行欠采样或对少数类别进行过度采样可以帮助均衡不平衡的数据集。
随机过采样(或者,随机欠采样)涉及在少数类中随机选择和复制观测值(或在多数类中随机选择和删除观测值)。
这很容易实现,但是您应谨慎行事:对采样重复的观测值进行过采样加权,如果不加偏见,可能会严重影响结果。 同样,采样不足会带来删除关键观测值的风险。
少数群体过采样的一种方法是合成少数群体过采样技术(SMOTE)。 这通过创建现有观测值的新组合来创建(综合)少数群体观测值。 对于少数群体类别中的每个观察,SMOTE会计算其k个最近的邻居; 也就是说,它找到最类似于该观测值的k个少数群体观测值。
通过将观察结果视为向量,它可以通过用0到1之间的随机数对k个最近邻居中的任何一个加权,并将其添加到原始向量中来创建随机线性组合。
多数类样本不足的一种方法是使用聚类质心。 从理论上讲,与SMOTE相似,它用k个最近邻居簇的质心替换向量组。
5. 贝叶斯统计
在统计推断方面,主要有两种思想流派:常客统计和贝叶斯统计。 频繁的统计数据使我们能够进行有意义的工作,但是在某些情况下,它的工作还不够。 当您有理由相信您的数据可能无法很好地表示您希望将来观察到的数据时,贝叶斯统计量会很好。
这使您可以将自己的知识整合到计算中,而不仅仅是依靠样本。 它还可以让您在收到新数据后更新对未来的看法。
来看一个例子:A队和B队互相比赛10次,A队赢得9次。 如果今晚两队互相比赛,我问你认为谁会赢,你可能会说A队! 如果我还告诉您B队贿赂了今晚的裁判怎么办? 好吧,那您可能会猜猜B队会赢。
贝叶斯统计允许您将这些额外的信息纳入您的计算中,而常客统计则仅关注10个获胜百分比中的9个。
贝叶斯定理是关键:
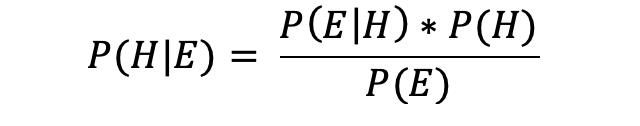
给定E的H的条件概率,记为P(H | E),表示当E也出现(或已经发生)时H发生的概率。 在我们的示例中,H是B队获胜的假设,E是我为您提供的有关B队贿赂裁判的证据。
P(H)是常客概率,为10%。 P(E | H)是在B队获胜的情况下我对您所说的关于贿赂的信息属实的概率。 (如果B队今晚获胜,您会相信我说的话吗?)
最后,P(E)是B队实际上贿赂裁判的概率。 我是值得信赖的信息来源吗? 您会发现,这种方法不仅包含了两支球队之前10场比赛的结果,而且还包含更多信息。
就是今天。 让我们在下一节中总结一下。
你走之前
学习这5个概念并不能使您掌握统计学或数据科学知识,但是如果您不了解数据科学项目的基本流程,那么这是一个很好的起点。