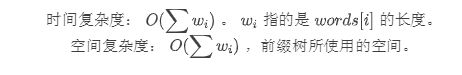前言
这次分享的Trie字典树,是数据结构专题中的一个分支,认识了解Trie这种树型数据结构,对构建算法与数据结构知识体系有一定的帮助。
我对Trie树的理解:把字符串都串接起来,消灭不必要的存储,利用的就是字符串的公共前缀。
其实对于它的理解,你理解了这句话即可👇
利用字符串的公共前缀来减少查询时间,最大限度的减少无谓的字符串比较,查询效率比哈希树高。
如果你还不了解什么是Trie数据结构的话,或者知道一些,但是对于它具体是如何实现一个简单Trie树时,那么这篇文章可能适合你阅读。
那么围绕以下几个点来展开介绍Trie树👇
- 基本概念
- 基本性质
- 应用场景
- 2个例题
基本概念
首先,我们对Trie树得做一些基本的了解。Trie树中文名叫字典树,前缀树等,接下来我就以字典树称呼。
我们来看下维基百科对它的描述吧⬇️
在计算机科学中,trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
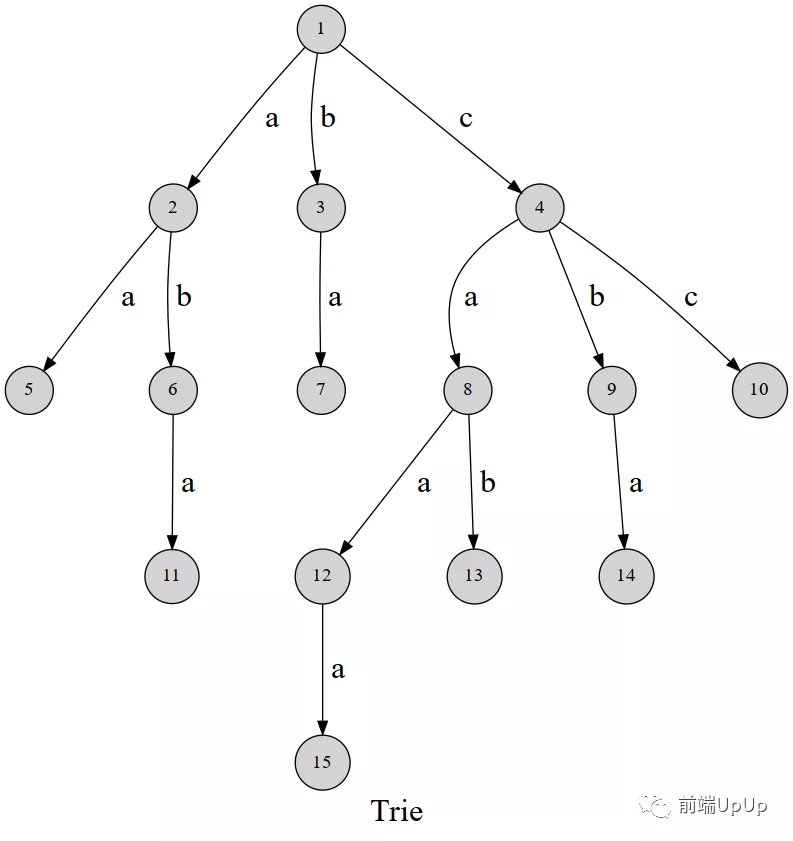
朴实无华的描述,其实我们看一张图就能看明白了~,我在网上找了一张不错的图,具体的出处,这里就不补充了,因为实在找不到原作者~
字典树图解1
这里需要说明的内容就是,一般而言,应该是用一个点来表示一个字符,这里为了更好的说明,所以我就是用边来描述字符。
可以发现,这棵字典树用边来代表字母,而从根结点到树上某一结点的路径就代表了一个字符串。举个例子, 1→2→6表示的就是字符串 aba 。
再比如,1→4→8构成的字符串是ca,那么如果在往下拓展的话,我们是不是有 caa,cab,那么他们都会经过1→4→8,这些路径,说明他们是有一段公共的前缀,这个前缀的内容就是ca,说道这里,我们就知道字典树利用的就是字符串的前缀来解决问题。
那么具体它有哪些性质的话,我们下文介绍一下~
基本性质
对于上述概念有了一定的理解后,我们接下来就看下Trie树的基本性质。
可以根据这个,大体上分成三个点来说👇
- 根节点不包含字符,除根节点外,每个节点只包含一个字符。
- 从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符串不相同。
接下来我们可以稍微分析一下,可以结合一个图来看看👇
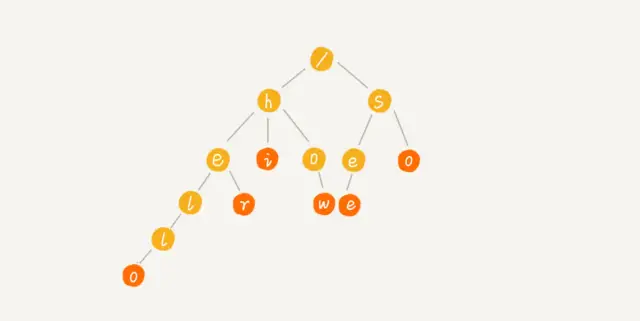
我们通过拿how,hi,her,hello,so,see这6个字符串构造出来的就是下面图这个样子。
图解Trie树
第一个性质:
从图中也可以看出,根节点是/, 代表的内容也就是空,其他的节点比如,根节点下一个层级,有 h和s,分别代表的是两个字符。
第二个性质:
从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
比如how表示的就是一个字符串,hi,也表示的是一个字符串,可是你会不会好奇,he和hel为什么不能表示一个字符串呢?
当你想到这里的话,说明你已经看得很仔细,马上就要掌握它了,确实,从图中看,我们会发现有些节点颜色不同,这是因为,我们预定好以这个深色的节点代表当前是一个字符串的结尾,想一想,这样子的作用是啥?
那么实际代码中,我们应该如何去约定或者做个标记呢,其实只要设置一个标记位即可。
比如下面这样子👇
- const TrieNode = function () {
- this.next = Object.create(null)
- this.isEnd = false
- };
当前的isEnd变量就表示当前的节点是不是结束串,当isEnd为True时,表示从根节点开始,到这个字符,所构成的字符串是存在的,是一个完整的字符串。
第三个性质:
每个节点的所有子节点包含的字符串不相同。
很明显,我们从根节点开始,依次往下走,会发现,每个节点下面的节点是不相同的,所以依次组成的字符串不可能相同。
应用场景
对Trie树,有一定了解后,我们就可以看看它有哪些的实际应用场景了。
这里参考的是网上所提供的几个点👇
在搜索引擎中关键词提示,引擎会自动弹出匹配关键词的下拉框,这种应用场景大家应该都很熟悉。
那么应该如何利用一种高效的数据结构存储呢,这里就符合字典树的性质,所以可以利用字典树来构造特定的数据,达到一种更加快速检索的效果。
字符串检索
事先将已知的一些字符串(字典)的有关信息保存到trie树里,查找另外一些未知字符串是否出现过或者出现频率,可以举例子说明情况👇
- 1000万字符串,其中有些是重复的,需要把重复的全部去掉,保留没有重复的字符串。
- 给出N 个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。
词频统计
给定很长的一个串,统计频数出现次数最多情况,举个例子👇
- 有一个1G大小的一个文件,里面每一行是一个词,词的大小不超过16字节,内存限制大小是1M。返回频数最高的100个词。
- 一个文本文件,大约有一万行,每行一个词,要求统计出其中最频繁出现的前10个词,请给出思想,给出时间复杂度分析。
字符串最长公共前缀
到现在,我们应该知道,Trie树利用多个字符串的公共前缀来节省存储空间,当我们把大量字符串存储到一棵trie树上时,我们可以快速得到某些字符串的公共前缀,所以可以利用这个特点来解决一些前缀问题。
非要举个例子的话,有个例子👇
- 给出N 个小写英文字母串,以及Q 个询问,即询问某两个串的最长公共前缀的长度是多少?
应用场景还是有很多的,剩下的可以自行去探索,接下来,我们通过实际的题目来看看,如何构造字典树吧~
2个例子
接下来,我们通过二个题目作为例子,来看看字典树在实际应用可以解决哪些问题👇
词典中最长的单词⭐
链接:词典中最长的单词
给出一个字符串数组words组成的一本英语词典。从中找出最长的一个单词,该单词是由words词典中其他单词逐步添加一个字母组成。若其中有多个可行的答案,则返回答案中字典序最小的单词。
若无答案,则返回空字符串。
示例 1:
- 输入:
- words = ["w","wo","wor","worl", "world"]
- 输出:"world"
- 解释:
- 单词"world"可由"w", "wo", "wor", 和 "worl"添加一个字母组成。
示例 2:
- 输入:
- words = ["a", "banana", "app", "appl", "ap", "apply", "apple"]
- 输出:"apple"
- 解释:
- "apply"和"apple"都能由词典中的单词组成。但是"apple"的字典序小于"apply"。
提示:
这题无非就是找到一个最长的单词,可以拆分成words数组中某一部分,最暴力的思路就是去枚举每一项,但是这样子的时间复杂度是巨大的, 这个时候,我们是不是可以思考一下,这个问题有哪些地方是共性的呢?
- 没错,就是前缀是相同的,从这点来看,是不是就可以利用这个前缀树,把它数据存储下来
- 然后遍历一遍字典树,只要这颗树只有一个分支,则表示它有解,如果存在两个分支以上的话,则无答案。
复杂度分析
这点应该很好理解,这里就跳过了。
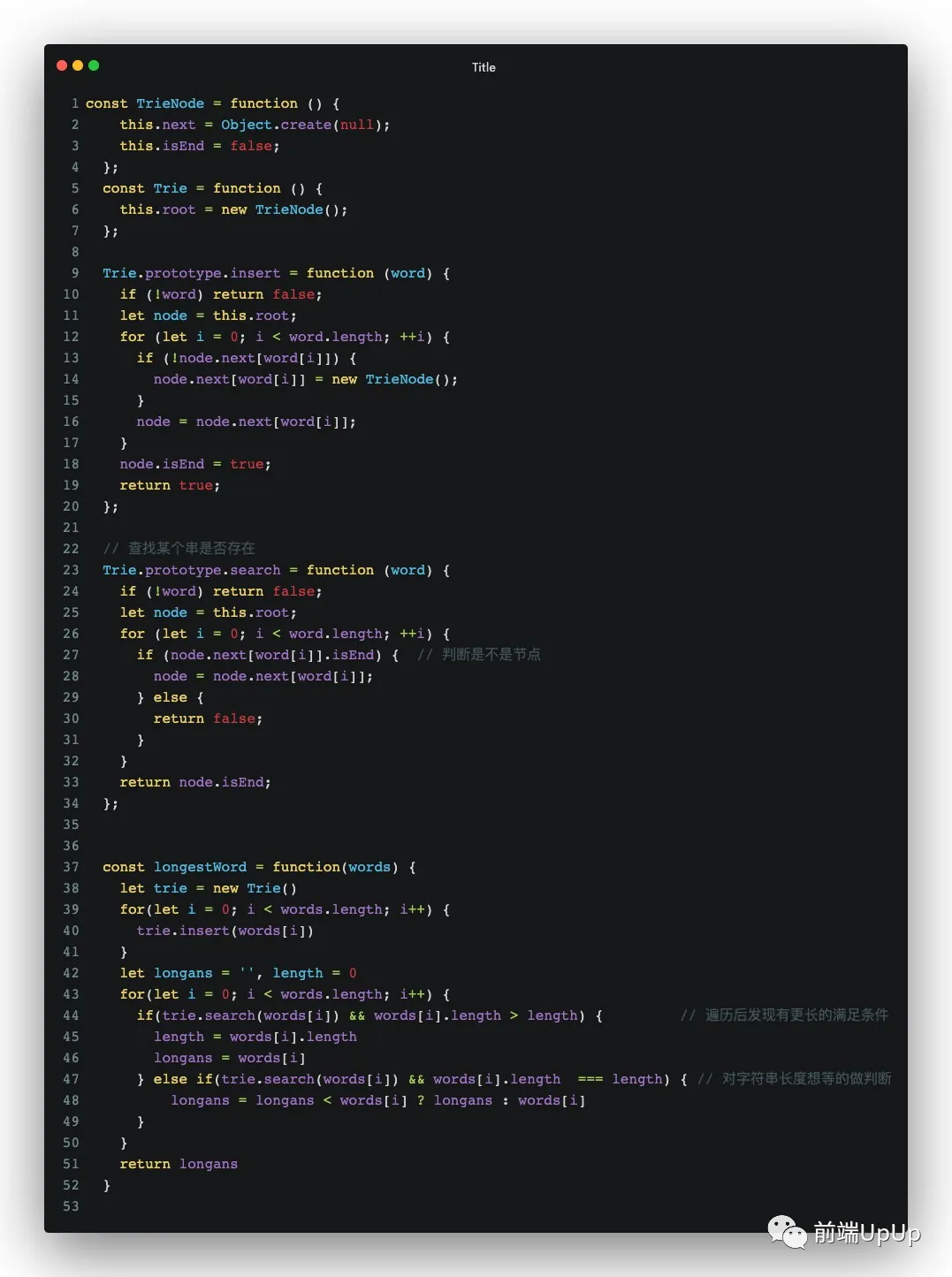
这里的话,我的解法构造字典树,当然了,也有其他的解法,这里就不展开了,可以看下我的代码噢~
代码点这里☑️
其实你会发现,构造一个Trie树的话,是很消耗空间的,有点空间换时间的意思,所以具体得根据实际的题目来解决问题。
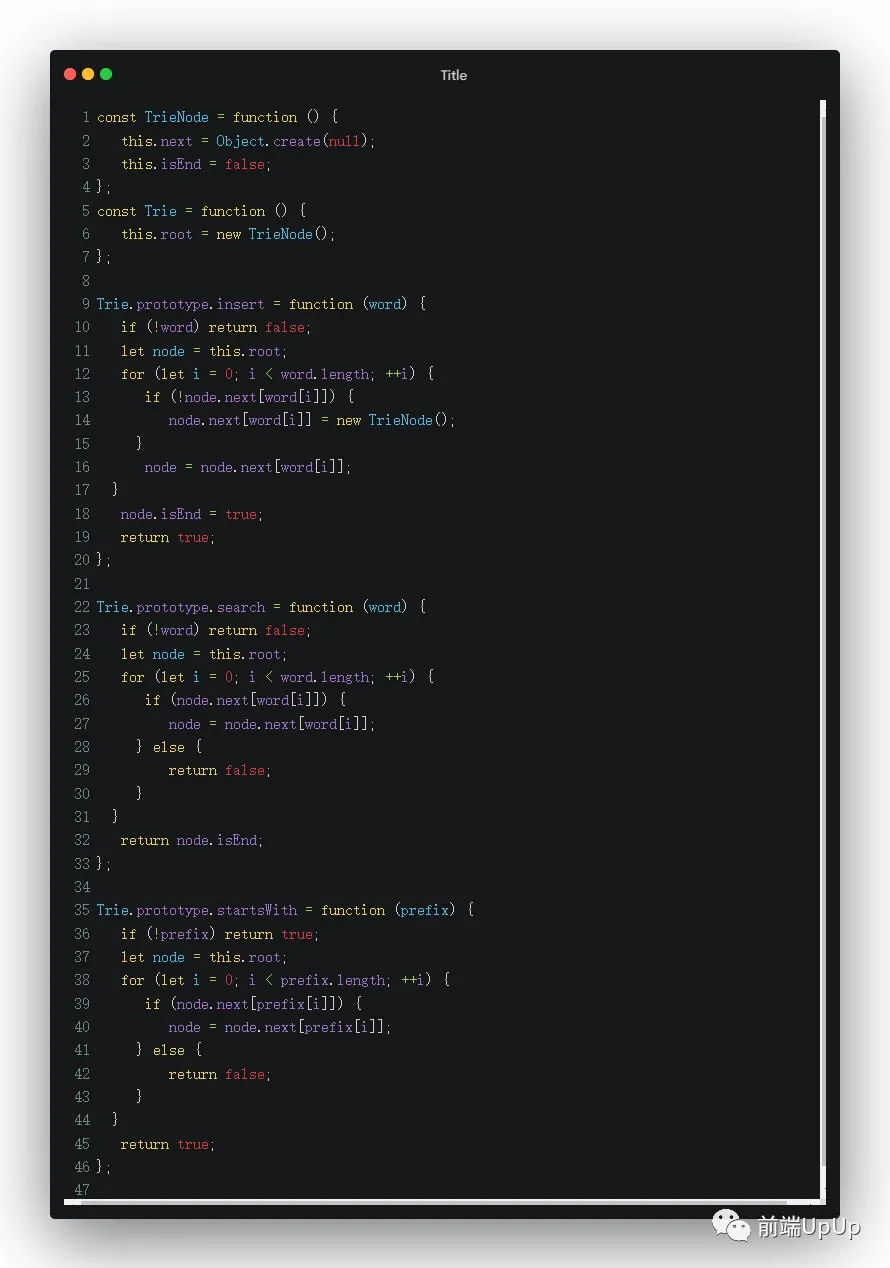
实现Trie(前缀树)⭐⭐
链接:实现 Trie (前缀树)
实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
- Trie trie = new Trie();
- trie.insert("apple");
- trie.search("apple"); // 返回 true
- trie.search("app"); // 返回 false
- trie.startsWith("app"); // 返回 true
- trie.insert("app");
- trie.search("app"); // 返回 true
说明:
- 你可以假设所有的输入都是由小写字母 a-z 构成的。
- 保证所有输入均为非空字符串。
这个题目就是典型的写Trie树,对于第一次写这个题目的话,如果没有思路的话,可以尝试先看看别人的代码,看看基本的套路在哪里。
话不多说,可以参考这份代码,可以看看如何构造一颗字典树👇
代码点这里☑️
剩下的删除操作,还有统计字符串出现的频率,可以自己来实现一下,这个基本上不难,画个图,就知道如何实现啦~
题目是做不完的,做完这些题目后,希望你能对Trie字典树有所认识,能对它有更加深入的理解~,接下来准备了四道题集,希望对你们有帮助~
词典中最长的单词
实现 Trie (前缀树)
单词搜索 II
Loading question