一种对机器学习系统进行分类的方法是看它们如何泛化。大多数机器学习任务是要做出预测。这意味着系统需要通过给定的训练示例,在它此前并未见过的示例上进行预测(泛化)。在训练数据上实现良好的性能指标固然重要,但是还不够充分。真正的目的是要在新的对象实例上表现出色。
泛化的主要方法有两种:基于实例的学习和基于模型的学习。
1. 基于实例的学习
我们最司空见惯的学习方法就是简单地死记硬背。如果以这种方式创建一个垃圾邮件过滤器,那么它可能只会标记那些与已被用户标记为垃圾邮件完全相同的邮件—这虽然不是最差的解决方案,但肯定也不是最好的。
除了完全相同的,你还可以通过编程让系统标记与已知的垃圾邮件非常相似的邮件。这里需要两封邮件之间的相似度度量。一种(基本的)相似度度量方式是计算它们之间相同的单词数目。如果一封新邮件与一封已知的垃圾邮件有许多单词相同,系统就可以将其标记为垃圾邮件。
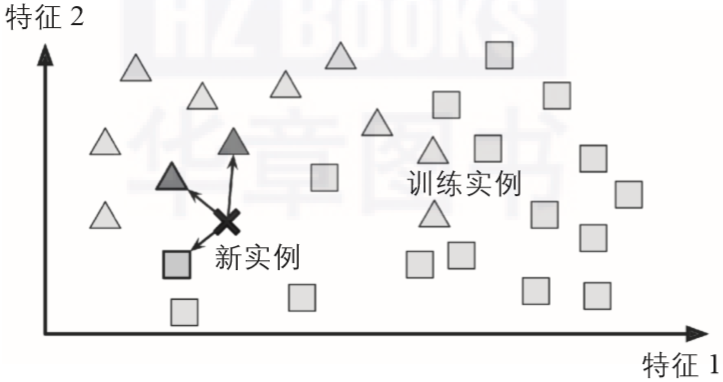
这被称为基于实例的学习:系统用心学习这些示例,然后通过使用相似度度量来比较新实例和已经学习的实例(或它们的子集),从而泛化新实例。例如,图1-15中的新实例会归为三角形,因为大多数最相似的实例属于那一类。
▲图1-15:基于实例的学习
2. 基于模型的学习
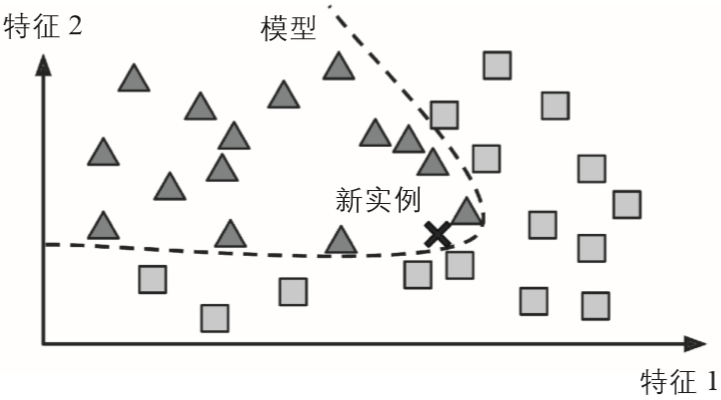
从一组示例集中实现泛化的另一种方法是构建这些示例的模型,然后使用该模型进行预测。这称为基于模型的学习(见图1-16)。
▲图1-16:基于模型的学习
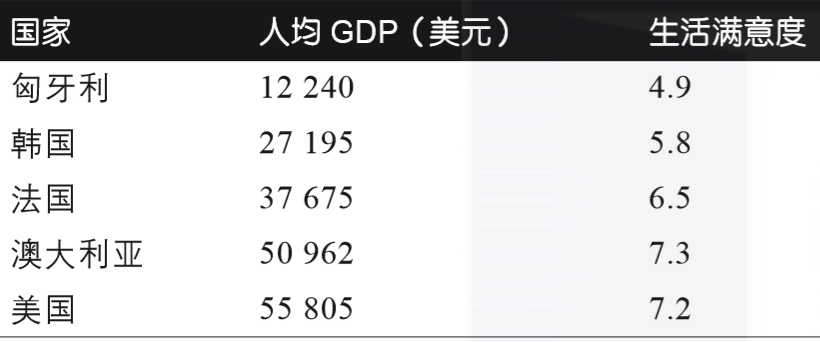
举例来说,假设你想知道金钱是否让人感到快乐,你可以从经合组织(OECD)的网站上下载“幸福指数”的数据,再从国际货币基金组织(IMF)的网站上找到人均GDP的统计数据,将数据并入表格,按照人均GDP排序,你会得到如表1-1所示的摘要。
表1-1:金钱能让人更快乐吗?
让我们绘制这些国家的数据(见图1-17)。
▲图1-17:趋势图
这里似乎有一个趋势!虽然数据包含噪声(即部分随机),但是仍然可以看出随着该国人均GDP的增加,生活满意度或多或少呈线性上升的趋势。所以你可以把生活满意度建模成一个关于人均GDP的线性函数。这个过程叫作模型选择。你为生活满意度选择了一个线性模型,该模型只有一个属性,就是人均GDP(见公式1-1)。
公式1-1:一个简单的线性模型
生活满意度= θ0 + θ1×人均GDP
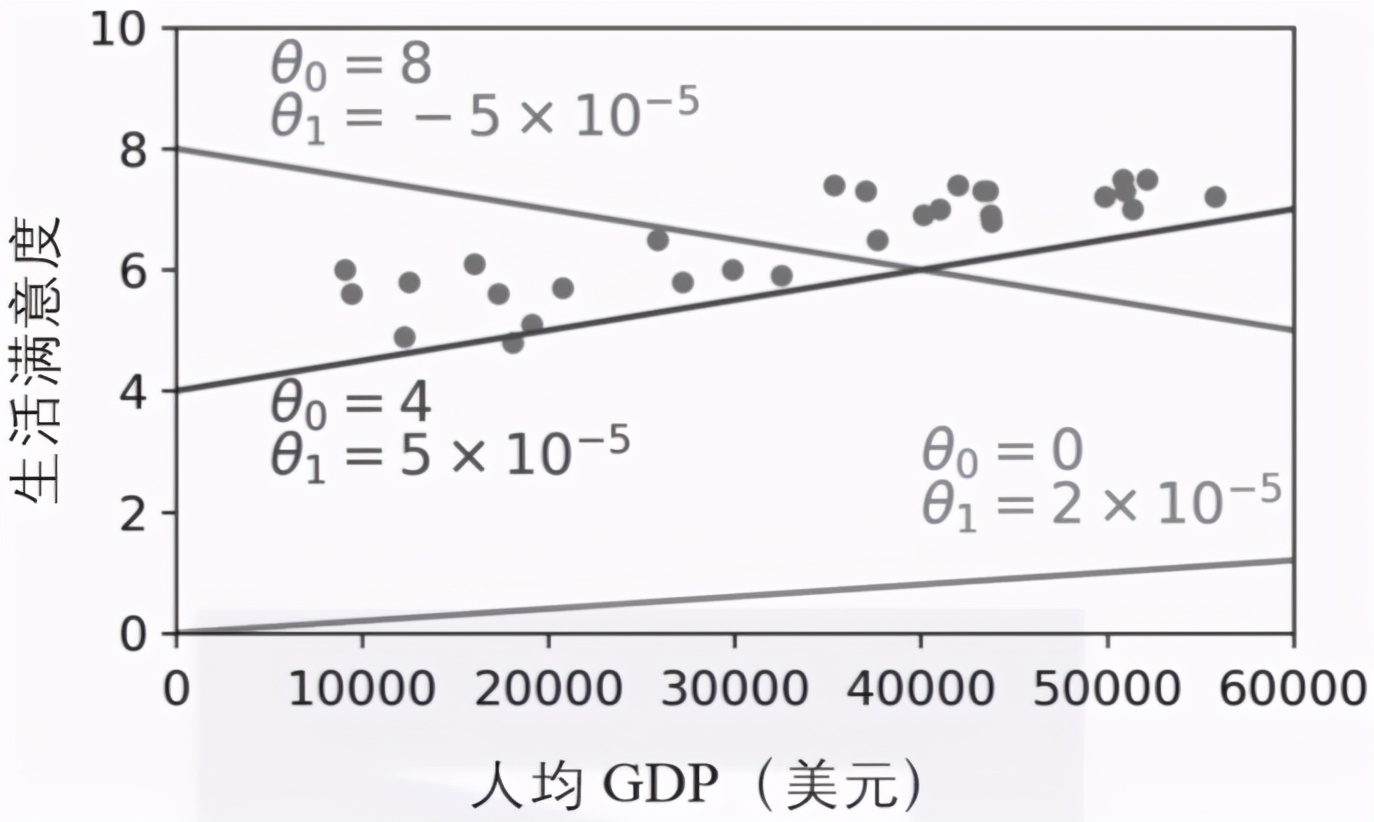
这个模型有两个模型参数:θ0和θ1。通过调整这两个参数,可以用这个模型来代表任意线性函数,如图1-18所示。
▲图1-18:一些可能的线性模型
在使用模型之前,需要先定义参数θ0和θ1的值。怎么才能知道什么值可以使模型表现最佳呢?要回答这个问题,需要先确定怎么衡量模型的性能表现。要么定义一个效用函数(或适应度函数)来衡量模型有多好,要么定义一个成本函数来衡量模型有多差。
对于线性回归问题,通常的选择是使用成本函数来衡量线性模型的预测与训练实例之间的差距,目的在于尽量使这个差距最小化。
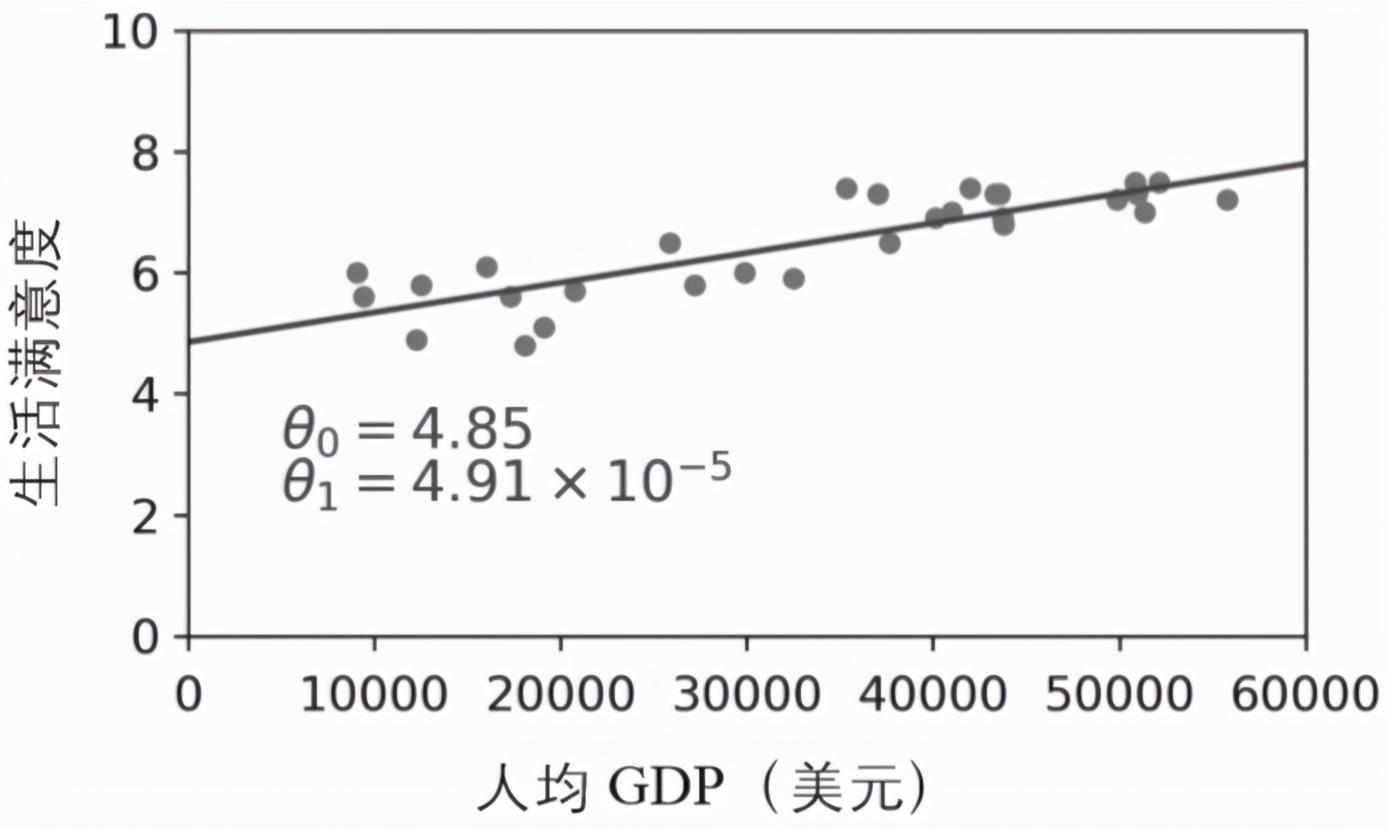
这正是线性回归算法的意义所在:通过你提供的训练样本,找出最符合提供数据的线性模型的参数,这称为训练模型。在这个案例中,算法找到的最优参数值为θ0 = 4.85和θ1 = 4.91×10^(-5)。
注意:令人困惑的是,同一个词“模型”可以指模型的一种类型(例如,线性回归),到一个完全特定的模型架构(例如,有一个输入和一个输出的线性回归),或者到最后可用于预测的训练模型(例如,有一个输入和一个输出的线性回归,使用参数θ0 = 4.85和θ1 = 4.91×10^(-5))。模型选择包括选择模型的类型和完全指定它的架构。训练一个模型意味着运行一种寻找模型参数的算法,使其最适合训练数据(希望能对新的数据做出好的预测)。
现在,(对于线性模型而言)模型基本接近训练数据,如图1-19所示。
▲图1-19:最拟合训练数据的线性模型
现在终于可以运行模型来进行预测了。例如,你想知道塞浦路斯人有多幸福,但是经合组织的数据没有提供答案。幸好你有这个模型可以做出预测:先查查塞浦路斯的人均GDP是多少,发现是22 587美元,然后应用到模型中,发现生活满意度大约是4.85 + 22 587×4.91×10^(-5) = 5.96。
为了激发你的兴趣,示例1-1是一段加载数据的Python代码,包括准备数据,创建一个可视化的散点图,然后训练线性模型并做出预测。
示例1-1:使用Scikit-Learn训练并运行一个线性模型
- import matplotlib.pyplot as plt
- import numpy as np
- import pandas as pd
- import sklearn.linear_model
- # Load the data
- oecd_bli = pd.read_csv("oecd_bli_2015.csv", thousands=',')
- gdp_per_capita = pd.read_csv("gdp_per_capita.csv",thousands=',',delimiter='\t',
- encoding='latin1', na_values="n/a")
- # Prepare the data
- country_stats = prepare_country_stats(oecd_bli, gdp_per_capita)
- X = np.c_[country_stats["GDP per capita"]]
- y = np.c_[country_stats["Life satisfaction"]]
- # Visualize the data
- country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction')
- plt.show()
- # Select a linear model
- model = sklearn.linear_model.LinearRegression()
- # Train the model
- model.fit(X, y)
- # Make a prediction for Cyprus
- X_new = [[22587]] # Cyprus's GDP per capita
- print(model.predict(X_new)) # outputs [[ 5.96242338]]
如果使用基于实例的学习算法,你会发现斯洛文尼亚的人均GDP最接近塞浦路斯(20 732美元),而经合组织的数据告诉我们,斯洛文尼亚人的生活满意度是5.7,因此你很可能会预测塞浦路斯的生活满意度为5.7。
如果稍微拉远一些,看看两个与之最接近的国家——葡萄牙和西班牙的生活满意度分别为5.1和6.5。取这三个数值的平均值,得到5.77,这也非常接近基于模型预测所得的值。这个简单的算法被称为k-近邻回归(在本例中,k = 3)。
要将前面代码中的线性回归模型替换为k-近邻回归模型非常简单,只需要将下面这行代码:
- import sklearn.linear_model
- model = sklearn.linear_model.LinearRegression()
替换为:
- import sklearn.neighbors
- model = sklearn.neighbors.KNeighborsRegressor(
- n_neighbors=3)
如果一切顺利,你的模型将会做出很棒的预测。如果不行,则需要使用更多的属性(例如就业率、健康、空气污染等),获得更多或更高质量的训练数据,或者选择一个更强大的模型(例如,多项式回归模型)。
简而言之:
- 研究数据。
- 选择模型。
- 使用训练数据进行训练(即前面学习算法搜索模型参数值,从而使成本函数最小化的过程)。
- 最后,应用模型对新示例进行预测(称为推断),希望模型的泛化结果不错。
以上就是一个典型的机器学习项目。