图
图形结构是一种比树形结构更复杂的非线性结构。在树形结构中,结点间具有分支层次关系,每一层上的结点只能和上一层中的至多一个结点相关,但可能和下一层的多个结点相关。而在图形结构中,任意两个结点之间都可能相关,即结点之间的邻接关系可以是任意的。
因此,图形结构被用于描述各种复杂的数据对象,在自然科学、社会科学和人文科学等许多领域有着非常广泛的应用 。图形结构在计算机科学、人工智能、电子线路分析、最短路径寻找、工程计划、化学化合物分析统计力学、遗传学、控制论语言学和社会科学等方面均有不同程度的应用可以这样说,图形结构在所有数据结构中应用最为广泛。如在地铁站中的线路图:
图的定义
图是一种数据结构,其中节点可以具有零个或多个相邻元素,两个节点的连接称之为边,节点在图形结构中也被称为顶点,一个顶点到另一个顶点的经过的的线路称为路径。
- 图形结构有3种类型:无向图、有向图、带权图
- 无向图:顶点A与顶点B之间的边是无方向的,可以从A到B,也可以从B到A
- 有向图:顶点A与顶点B之间的边是有方向的,可以从A到B,但不可以从B到A
- 带权图:顶点A与顶点B之间的边是带有属性的,如A到B的 距离。
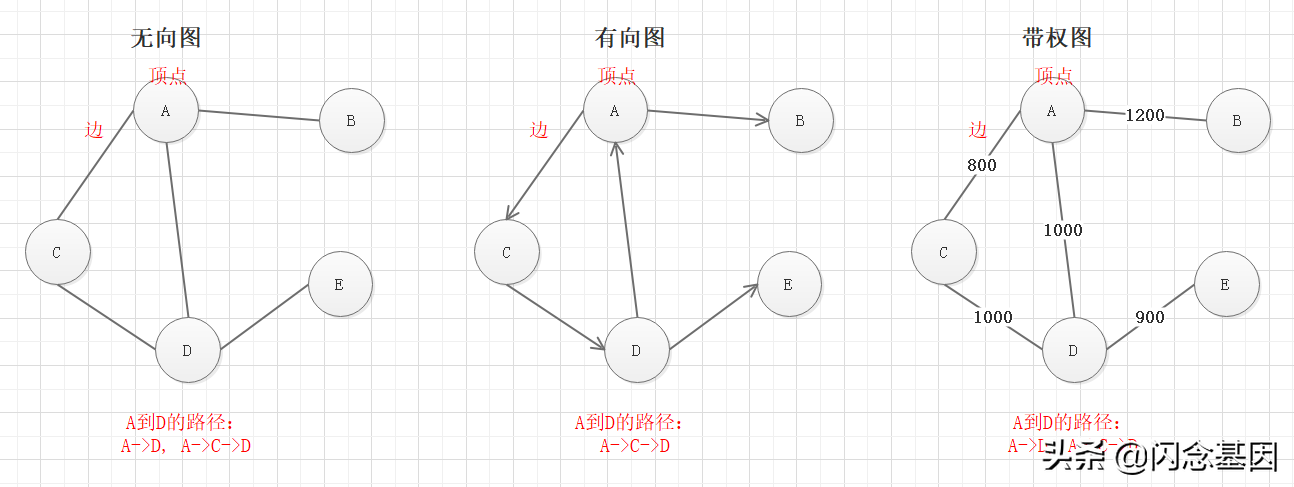
图的表达方式
图的表达方式有两种:邻接矩阵(使用二维数组)和邻接表(使用数组+链表)
邻接矩阵
邻接矩阵是表示图形中各顶点之间的关系,矩阵的行和列对应各顶点,坐标位置上的值对于它们之间的关系,1为连接, 0为没有连接。在程序中用二维数组来实现。
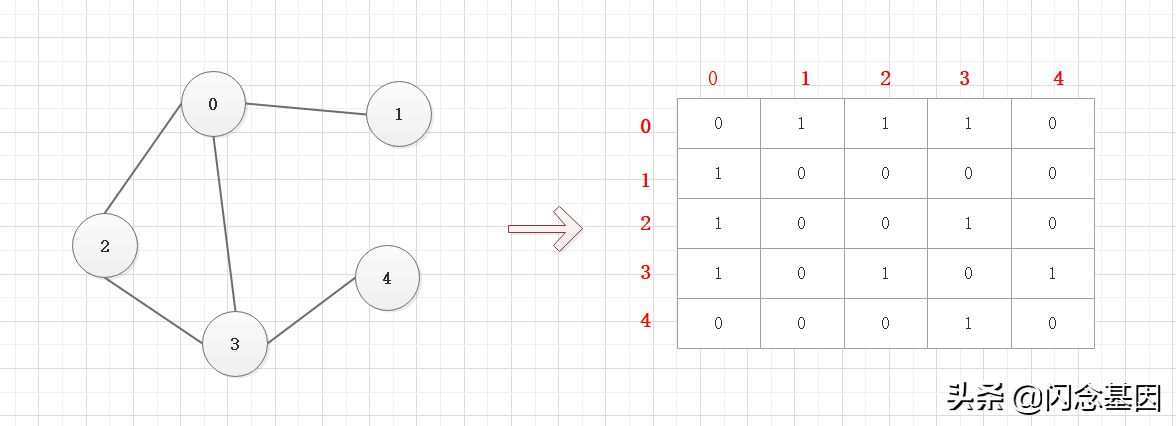
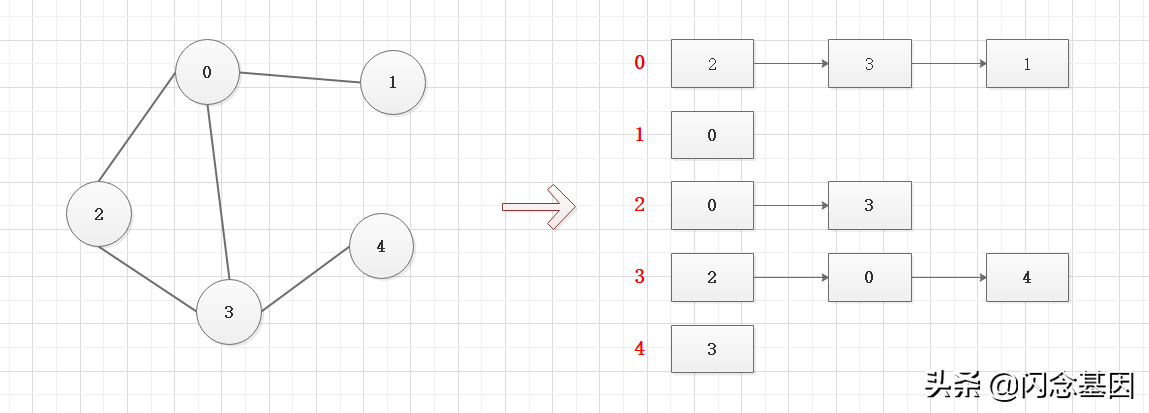
邻接表
邻接表只关系存在的边,不需要去为不存在的边分配空间,因此比邻接矩阵来说,避免了不必要的空间浪费。在程序中用数组+链表的形式实现,数组存储对应的顶点,链表存储该顶点连接的所有顶点。
图的搜索算法
图形结构基础属性和方法
以下的代码演示都是以邻接矩阵表达方式来实现的
- //图形结构(邻接矩阵)
- class Graph {
- //存储图中所有顶点
- private List<String> vertexes;
- //图形结构的邻接矩阵
- private int[][] matrix;
- //各顶点访问情况,true为已访问,false为未访问
- private boolean[] visited;
- /**
- * 根据传入的顶点信息生成矩阵
- * @param s
- */
- public Graph(String s[]) {
- vertexes = new ArrayList<>();
- for (String vertex : s){
- vertexes.add(vertex);
- }
- matrix = new int[s.length][s.length];
- }
- /**
- * 将俩个顶点连接,即生成边
- * @param index1 顶点在集合中的索引
- * @param index2
- */
- public void connect(int index1, int index2){
- if (index1 < 0 || index1 > matrix.length || index2 < 0 || index2 > matrix.length){
- throw new RuntimeException("该顶点未存在");
- }
- //将新的邻接添加的邻接矩阵中
- matrix[index1][index2] = 1;
- matrix[index2][index1] = 1;
- }
- /**
- * 展示邻接矩阵
- */
- public void showGraphMatrix(){
- for (int arr[] : matrix){
- System.out.println(Arrays.toString(arr));
- }
- }
- /**
- * 获取顶点在邻接矩阵对应行row中的第一个邻接顶点下标
- * @param row
- * @return 当有邻接顶点时返回邻接顶点下标,没有则返回-1
- */
- public int getFirstNeighbor(int row){
- for(int i =0; i<matrix.length; i++){
- if (matrix[row][i] != 0){
- return i;
- }
- }
- return -1;
- }
- /**
- * 获取顶点在邻接矩阵对于行row中col列的下一个邻接顶点
- * @param row
- * @param col
- * @return 当有邻接顶点时返回邻接顶点下标,没有则返回-1
- */
- public int getNeighbor(int row, int col){
- for (int i=col+1; i<matrix.length; i++){
- if (matrix[row][i] != 0){
- return i;
- }
- }
- return -1;
- }
- }
深度优先搜索
深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。这样的访问策略是优先往纵向进行深入挖掘,而不是对一个顶点的所有邻接顶点进行横线访问。简单来说就是一条路走到死,不行再掉头。
思路:从当前顶点选一个与之连接而未访问过的顶点,将当前节点往该邻接顶点移动,如果邻接顶点没有未访问的,则回溯到上一个顶点位置,继续该步骤。直到所有顶点都访问过。
往邻接但未访问过的顶点移动
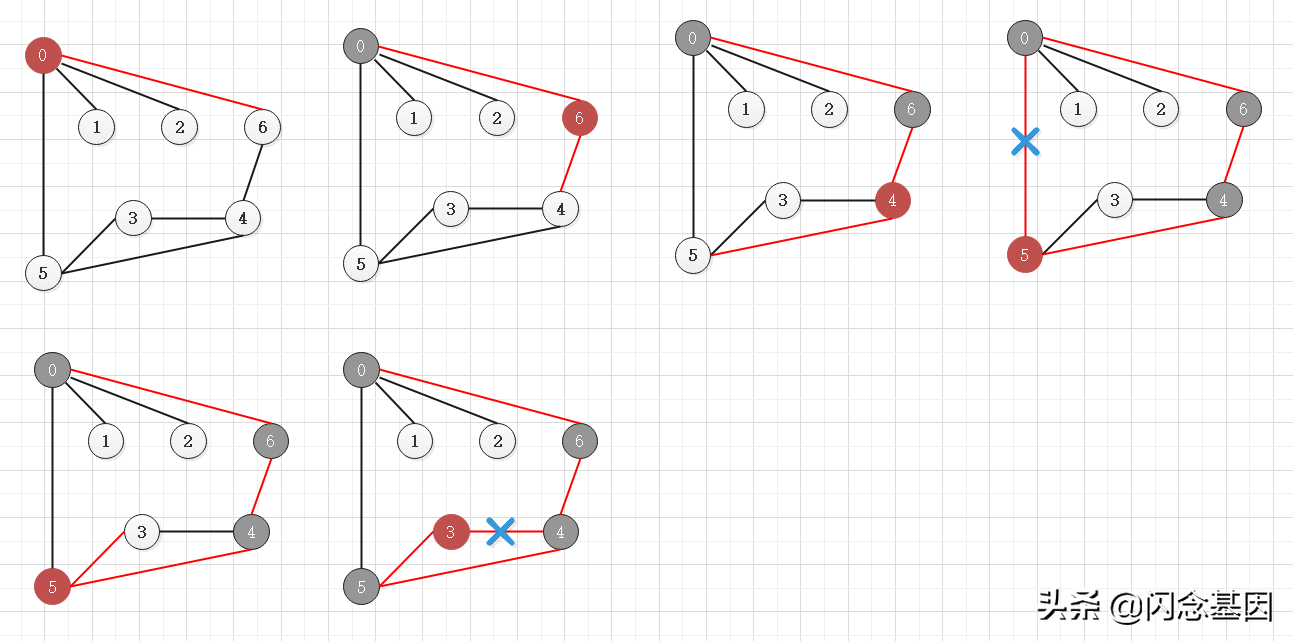
邻接顶点没有未访问的,进行回溯,直到遇到未访问的邻接顶点
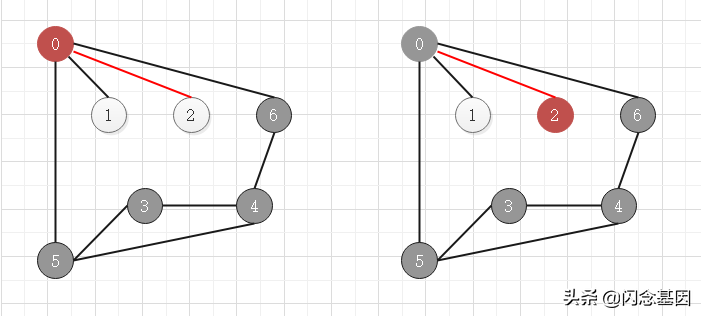
当所有顶点都被访问过时,退出算法
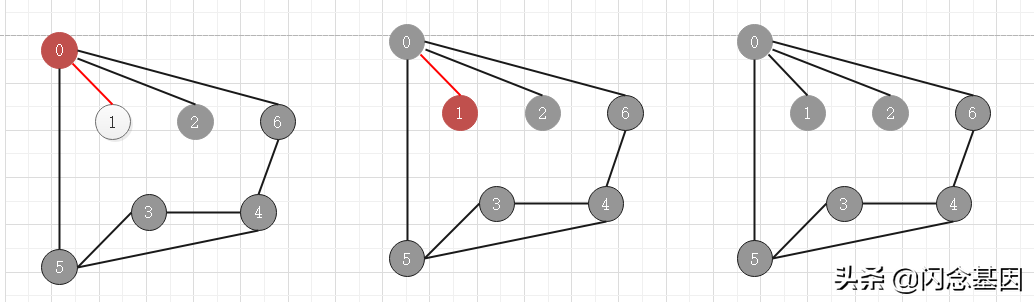
下面是深度优先搜索的过程动画
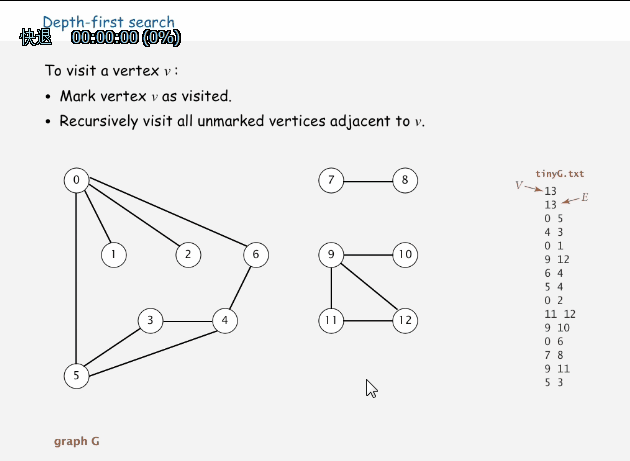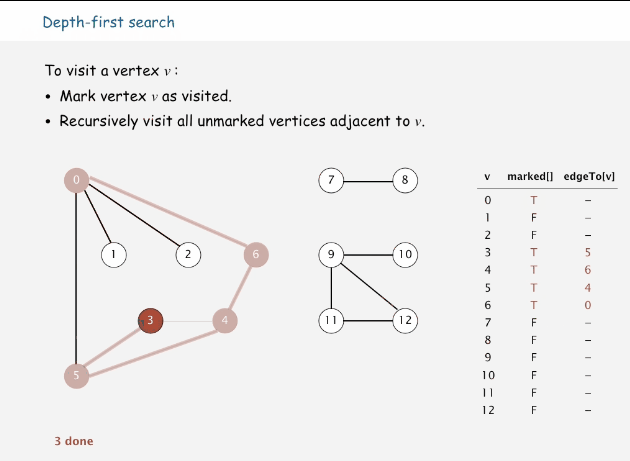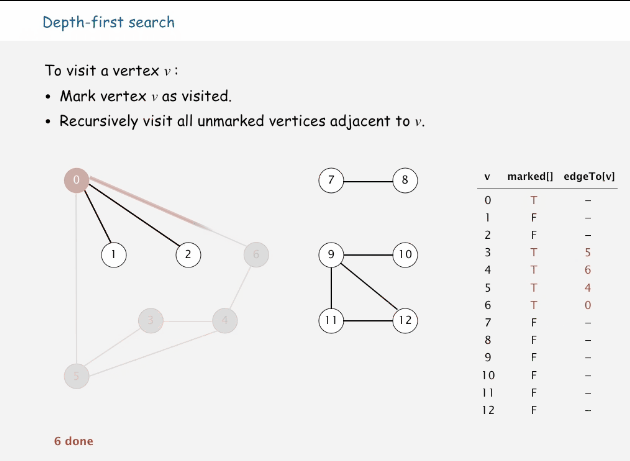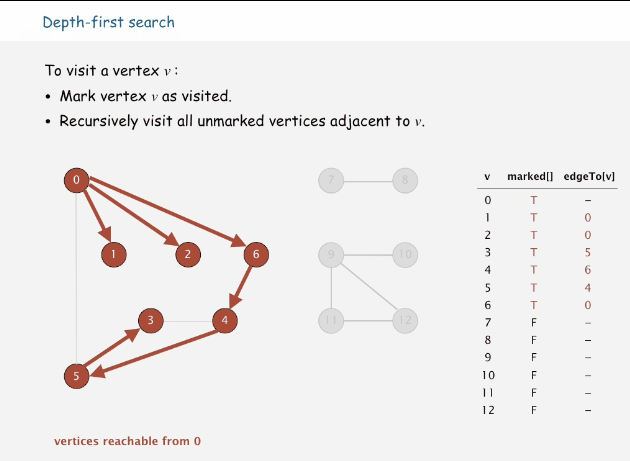
代码演示
- public void dsf(){
- visited = new boolean[vertexes.size()];
- //以在集合中下标为0的顶点,进行深度搜索
- dsf(visited, 0);
- }
- /**
- * 深度优先搜索
- * @param visited
- * @param row
- */
- public void dsf(boolean[] visited, int row){
- //输出当前顶点
- System.out.print(vertexes.get(row) + " -> ");
- //将当前顶点设为已访问
- visited[row] = true;
- //获取当前顶点的邻接顶点下标
- int index = getFirstNeighbor(row);
- //如果当前顶点有邻接顶点则进行深度搜索
- while (index != -1){
- //当邻接顶点未访问时,则递归遍历
- if (visited[index] != true){
- dsf(visited, index);
- }
- //当邻接顶点已访问时,则寻找另一个邻接顶点
- index = getNeighbor(row, index);
- }
- }
宽度优先搜索
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
宽度优先搜索算法类似于一个分层搜索的过程,宽度优先搜索算法需要一个队列以保持访问过顶点的顺序,以便按这个顺序来访问这些顶点的邻接顶点。
思路:依次访问当前顶点的邻接顶点,并按访问顺序将这些邻接顶点存储在队列中,当当前顶点的所有邻接顶点都被访问后,从队列中弹出一个顶点,以该顶点为当前顶点继续该步骤,直到所有顶点都被访问过。
依次访问当前顶点的所有邻接顶点,并把这些邻接顶点按访问顺序存储在队列中
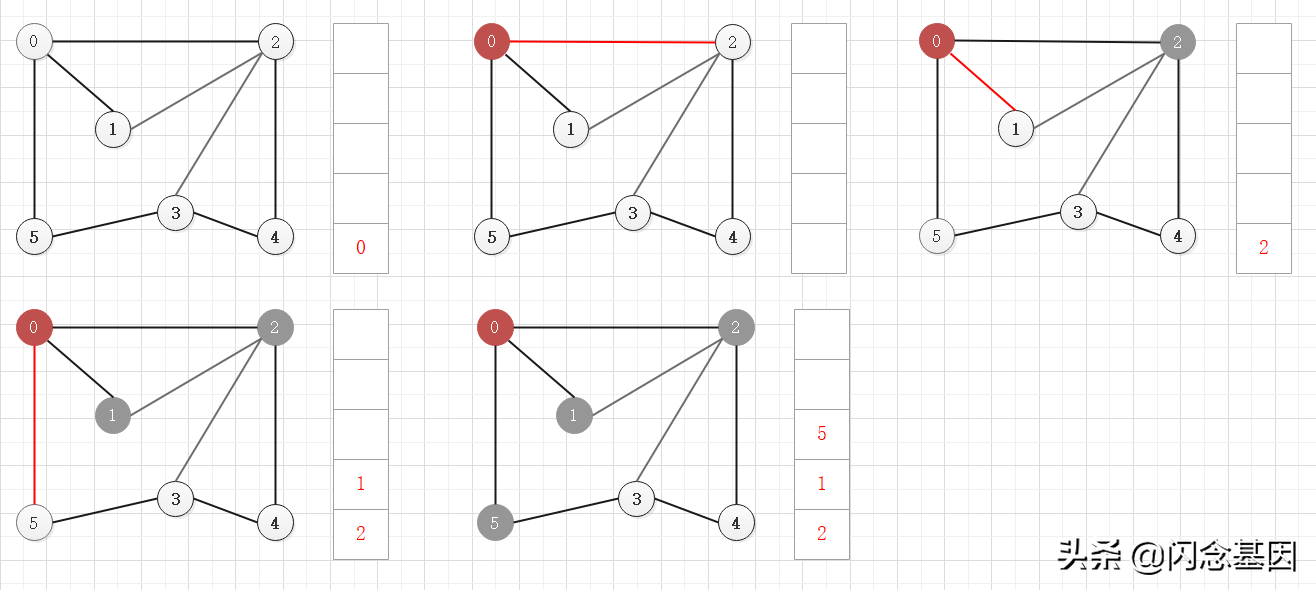
当前顶点没有未访问的邻接顶点,从队列中弹出一个顶点,以该弹出顶点继续访问未访问的邻接顶点
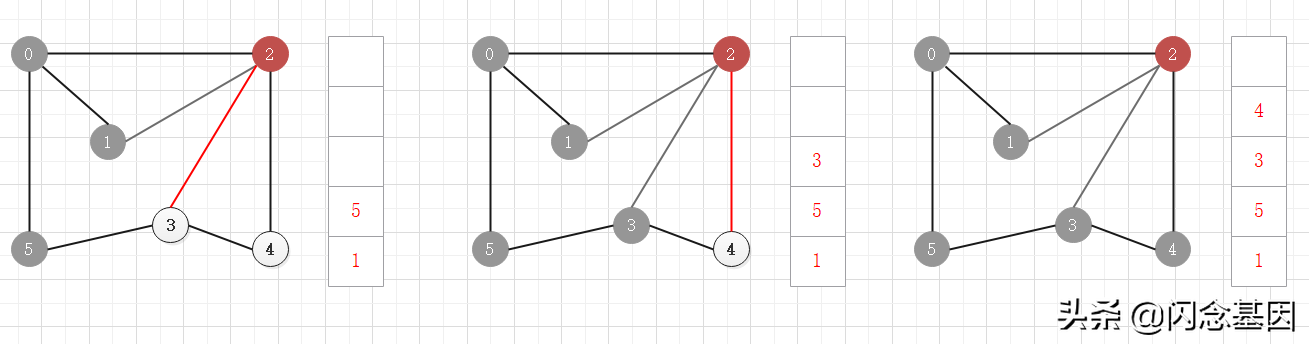
注意,虽然图中的顶点都已经访问过了,但还是要等队列中的所有顶点弹出访问后,算法才结束

下面时宽度优先搜索的过程动画
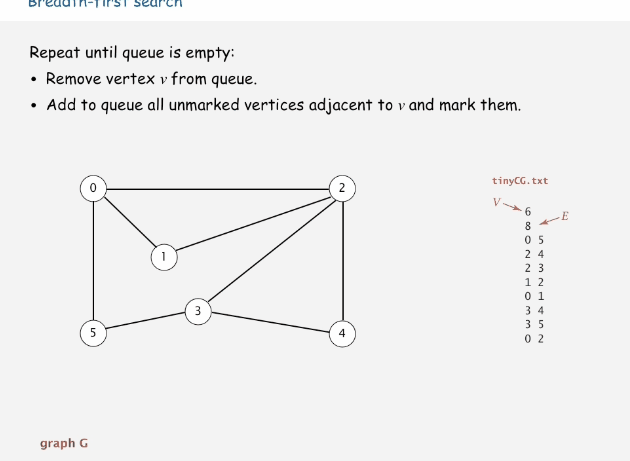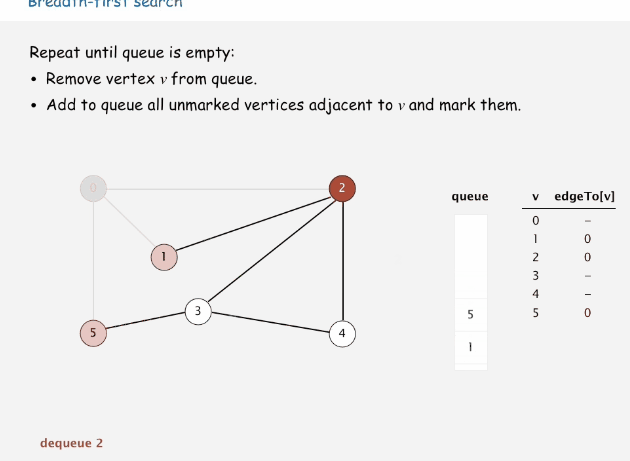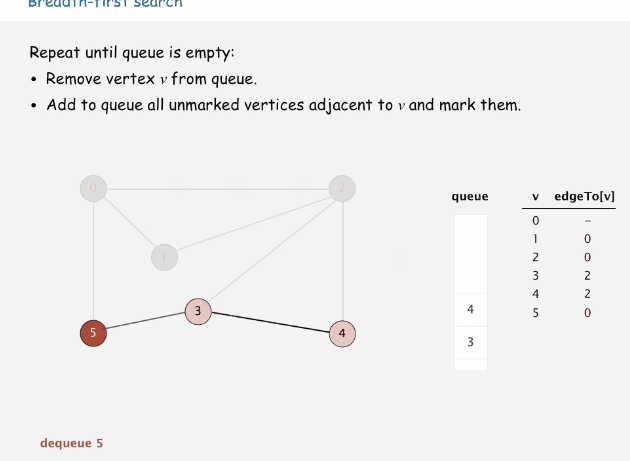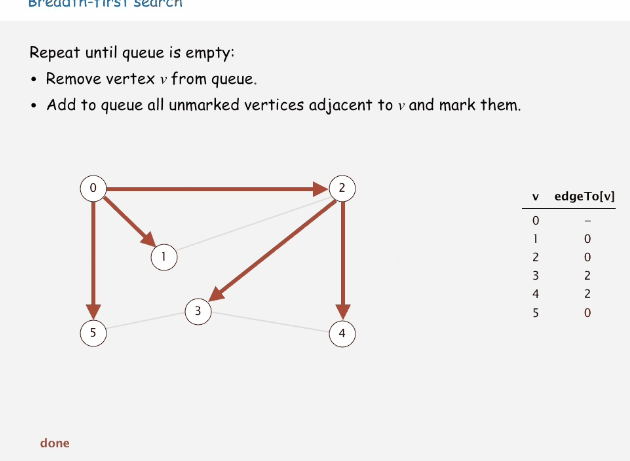
代码演示
- public void bfs(){
- visited = new boolean[vertexes.size()];
- ////以在集合中下标为0的顶点,进行广度优先搜索
- bfs(visited, 0);
- }
- /**
- * 广度优先搜索
- * @param visited
- * @param row
- */
- public void bfs(boolean[] visited, int row){
- //创建队列,存储遍历邻接顶点的顺序
- LinkedList queue = new LinkedList();
- //输出当前顶点
- System.out.print(vertexes.get(row) + " -> ");
- //将当前顶点设为已访问
- visited[row] = true;
- //将当前顶点加入队列中
- queue.add(row);
- //当队列不为空时,即有未搜索的邻接顶点,进行搜索
- while (!queue.isEmpty()){
- //按顺序从队列中弹出邻接顶点下标
- int last = (Integer)queue.removeFirst();
- //获取该弹出顶点的邻接顶点下标
- int index = getFirstNeighbor(last);
- //当弹出顶点有邻接顶点时,进行广度搜索
- while(index != -1){
- //当邻接顶点未访问时
- if(visited[index] != true){
- //输出该邻接顶点
- System.out.print(vertexes.get(index) + " -> ");
- //把该邻接顶点设为已访问
- visited[index] = true;
- //将该邻接顶点加入队列
- queue.addLast(index);
- }
- //继续寻找弹出顶点的另一个邻接顶点
- index = getNeighbor(last, index);
- }
- }
- }
完整演示代码
- public class GraphDemo {
- public static void main(String[] args) {
- String[] s = {"A","B","C","D","E","F","G"};
- Graph graph = new Graph(s);
- //A-B A-C A-G A-F F-D F-E D-E E-G
- graph.connect(0, 1);
- graph.connect(0, 2);
- graph.connect(0, 6);
- graph.connect(0, 5);
- graph.connect(5, 3);
- graph.connect(5, 4);
- graph.connect(3, 4);
- graph.connect(4, 6);
- graph.showGraphMatrix();
- graph.dsf();//A -> B -> C -> F -> D -> E -> G ->
- System.out.println();
- graph.bfs();//A -> B -> C -> F -> G -> D -> E ->
- }
- }
- //图形结构
- class Graph {
- //存储图中所有顶点
- private List<String> vertexes;
- //图形结构的邻接矩阵
- private int[][] matrix;
- //各顶点访问情况,true为已访问,false为未访问
- private boolean[] visited;
- /**
- * 根据传入的顶点信息生成矩阵
- * @param s
- */
- public Graph(String s[]) {
- vertexes = new ArrayList<>();
- for (String vertex : s){
- vertexes.add(vertex);
- }
- matrix = new int[s.length][s.length];
- }
- /**
- * 将俩个顶点连接,即生成边
- * @param index1 顶点在集合中的索引
- * @param index2
- */
- public void connect(int index1, int index2){
- if (index1 < 0 || index1 > matrix.length || index2 < 0 || index2 > matrix.length){
- throw new RuntimeException("该顶点未存在");
- }
- //将新的邻接添加的邻接矩阵中
- matrix[index1][index2] = 1;
- matrix[index2][index1] = 1;
- }
- /**
- * 展示邻接矩阵
- */
- public void showGraphMatrix(){
- for (int arr[] : matrix){
- System.out.println(Arrays.toString(arr));
- }
- }
- public void dsf(){
- visited = new boolean[vertexes.size()];
- //以在集合中下标为0的顶点,进行深度优先搜索
- dsf(visited, 0);
- }
- /**
- * 深度优先搜索
- * @param visited
- * @param row
- */
- public void dsf(boolean[] visited, int row){
- //输出当前顶点
- System.out.print(vertexes.get(row) + " -> ");
- //将当前顶点设为已访问
- visited[row] = true;
- //获取当前顶点的邻接顶点下标
- int index = getFirstNeighbor(row);
- //如果当前顶点有邻接顶点则进行深度搜索
- while (index != -1){
- //当邻接顶点未访问时,则递归遍历
- if (visited[index] != true){
- dsf(visited, index);
- }
- //当邻接顶点已访问时,则寻找另一个邻接顶点
- index = getNeighbor(row, index);
- }
- }
- public void bfs(){
- visited = new boolean[vertexes.size()];
- ////以在集合中下标为0的顶点,进行广度优先搜索
- bfs(visited, 0);
- }
- /**
- * 广度优先搜索
- * @param visited
- * @param row
- */
- public void bfs(boolean[] visited, int row){
- //创建队列,存储遍历邻接顶点的顺序
- Queue queue = new ArrayDeque();
- //输出当前顶点
- System.out.print(vertexes.get(row) + " -> ");
- //将当前顶点设为已访问
- visited[row] = true;
- //将当前顶点加入队列中
- queue.add(row);
- //当队列不为空时,即有未搜索的邻接顶点,进行搜索
- while (!queue.isEmpty()){
- //按顺序从队列中弹出邻接顶点下标
- int last = (Integer)queue.poll();
- //获取该弹出顶点的邻接顶点下标
- int index = getFirstNeighbor(last);
- //当弹出顶点有邻接顶点时,进行广度搜索
- while(index != -1){
- //当邻接顶点未访问时
- if(visited[index] != true){
- //输出该邻接顶点
- System.out.print(vertexes.get(index) + " -> ");
- //把该邻接顶点设为已访问
- visited[index] = true;
- //将该邻接顶点加入队列
- queue.add(index);
- }
- //继续寻找弹出顶点的另一个邻接顶点
- index = getNeighbor(last, index);
- }
- }
- }
- /**
- * 获取顶点在邻接矩阵对应行row中的第一个邻接顶点下标
- * @param row
- * @return 当有邻接顶点时返回邻接顶点下标,没有则返回-1
- */
- public int getFirstNeighbor(int row){
- for(int i =0; i<matrix.length; i++){
- if (matrix[row][i] != 0){
- return i;
- }
- }
- return -1;
- }
- /**
- * 获取顶点在邻接矩阵对于行row中col列的下一个邻接顶点
- * @param row
- * @param col
- * @return 当有邻接顶点时返回邻接顶点下标,没有则返回-1
- */
- public int getNeighbor(int row, int col){
- for (int i=col+1; i<matrix.length; i++){
- if (matrix[row][i] != 0){
- return i;
- }
- }
- return -1;
- }
- }







































