前言
这次分享的内容是,经典算法思想-分治,你可以把它称之为一种思想,也可以叫它分治算法,为了更好的区分,接下来我们以'分治法'来称呼它。
如果你还不了解什么是分治法,或者知道一些,但是对于它具体是如何实现回溯,那么这篇文章可能适合你阅读。
我对分治算法的理解:
- 它的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。
- 求出子问题的解,就可得到原问题的解,可以理解成一种分目标完成程序的算法。
- 二分法很多时候,就是一种分治的思想。
那么围绕以下几个点来展开介绍分治算法👇
- 基本思路
- 适用情况以及求解哪些经典问题
- 经典例题
分治法基本思想
一句话,对分治法概括它的话👇
将原问题划分成n个规模较小而结构与原问题相似的子问题,递归去解决这些子问题,然后依次再合并其结果,最后得到原问题的解。
那么具体的来说,我们似乎可以分成三个步骤👇
- 分解:将要解决的问题划分成若干规模较小的同类问题。
- 解决:当子问题划分得足够小时,用较简单的方法解决。
- 合并:按原问题的要求,将子问题的解逐层合并构成原问题的解。
其实思想还是不变的,将一个难以直接解决的大问题,分割成一些小规模的相同问题,以便各个击破,分而治之。
分治法适用情况
利用分治法求解一个问题,在于我们能否掌握分治法的几个特征:
- 把一个问题可以缩小到一定程度,变成更小的问题来解决。
- 分解成若干个小问题后,规模更小且是同类问题,这样子的话,该问题应该就是最优子结构。
- 利用该问题分解出来的子问题的解,合并为该问题的解。
- 分解出来的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
那我们来说一说这几个特征吧~
第一条特征:一个问题的计算复杂性一般是随问题的规模增加而增加的,所以绝大多数问题都满足。
第二条特征:应用分治法的前提是得满足它,你可以理解成它某种程度上反映了递归思想的应用。
第三条特征:这个应该就是分治法的关键了吧,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法。
第四条特征:涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
了解分治法的特征,我们来看看有哪些经典的问题是利用这个思想来解决问题的👇
分治法求解经典问题
什么情况下,可以用该思路来求解呢,以下来自网上搜集的内容👇
(1)二分搜索
(2)大整数乘法
(3)Strassen矩阵乘法
(4)棋盘覆盖
(5)合并排序
(6)快速排序
(7)线性时间选择
(8)最接近点对问题
(9)循环赛日程表
(10)汉诺塔
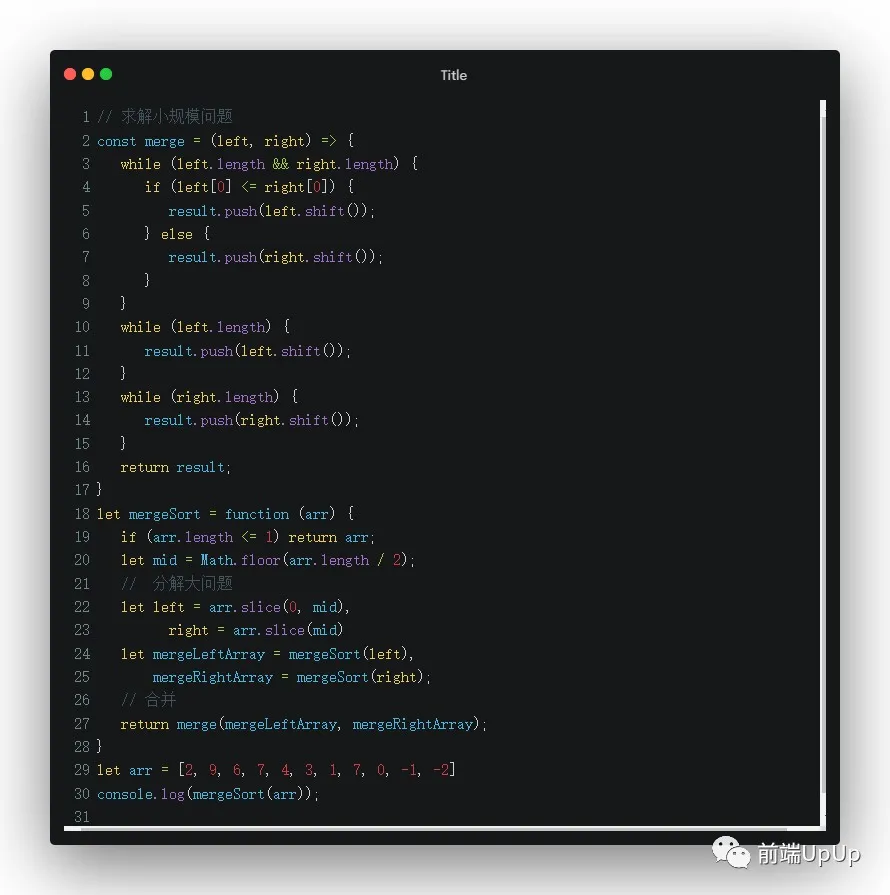
我想提起的是合并(归并)排序,它完成照应分治法的思想,分解大问题,解决各个规模小问题,最后合并,那我们来看看合并(归并)排序代码👇
归并排序
对于归并排序的思路,是如何实现的,之前的排序一章以及提及过,采用的是分治思路,可以看看是如何实现的,这里就不具体展开了。
2个例子
接下来,我们通过三个题目作为例子,来看看怎么利用分治的思想来解决问题👇
最大子序和⭐
链接:最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/maximum-subarray 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
首先,我们看看能不能以O(n)复杂度解决这个问题,其实仔细想一想的话,我们可以通过一个简单
更多得是,我们这题尝试一下用分治法来解决这题。对于一个数组的最大子序和,它对答案的贡献,只能是以下几种情况👇
- 出现在左半边
- 出现在右半边
- 出现在中间,穿过中间。
那么我们是不是可以递归处理呢,对于出现在左边和出现在右边的答案,我们可以把它们当作是一种情况,然后递归去处理,当然了递归的出口,很显然,当递归的数组的长度为1时,我们需要递归结束。
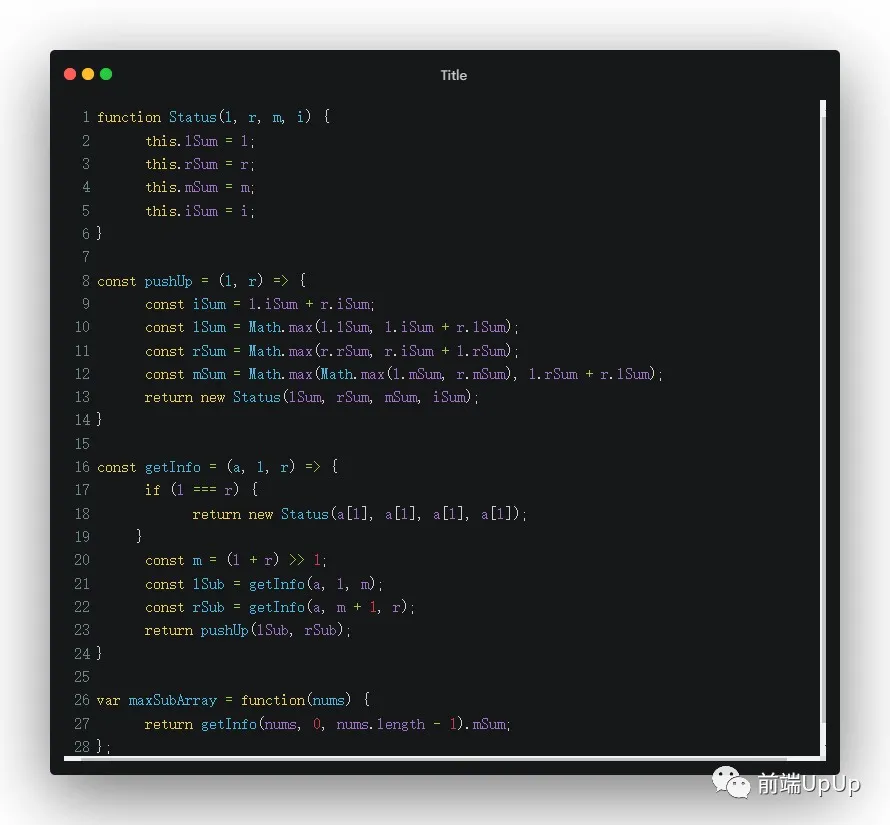
对于出现在中间答案的情况,我们可以通过计算来算出答案,所以思路理清楚, 接下来,我们看如何写👇
分治法连续最大和
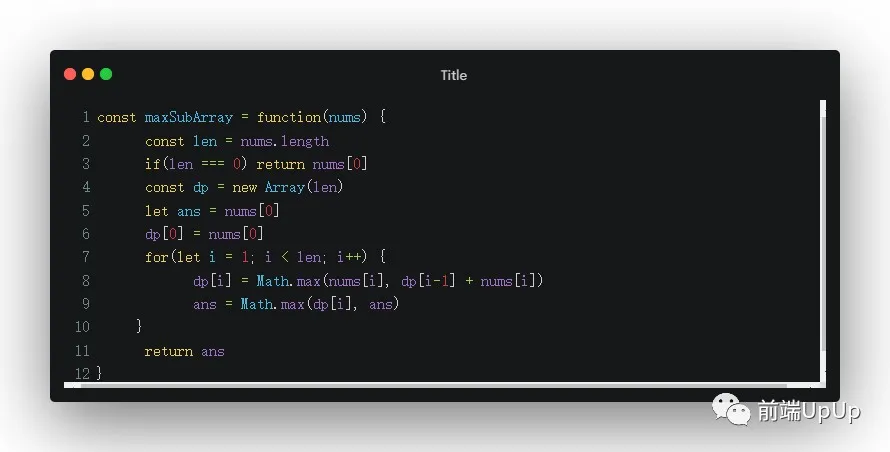
当然了,这题用动态规划思路更好求解,也更加得好理解👇
- //dp[i]表示nums中以nums[i]结尾的最大子序和
动态规划求连续和
代码点这里☑️
搜索二维矩阵 II⭐⭐
链接:搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
每行的元素从左到右升序排列。每列的元素从上到下升序排列。示例:
现有矩阵 matrix 如下:
- [ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/search-a-2d-matrix-ii 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这题的题目很清晰👉矩阵的每行从左到右是升序, 每列从上到下也是升序,在矩阵中查找某个数。
当然了,我们有一个简单的思路👇
- 维护两个指针(row,col),找到目标元素时,我们就放回true
- 当指向当前的元素值小于target时,我们就col++,向上移动一行。
- 如果当前的值大于当前的target,我们就row--,向左移动一列。
- 知道col > 矩阵的行,或者row < 0时,我们直接return false,表示不存在。
时间复杂度:O(n+m)
- 时间复杂度分析的关键是注意到在每次迭代(我们不返回 true)时,行或列都会精确地递减/递增一次。
- 由于行只能减少 m 次,而列只能增加 n次,因此在导致 while 循环终止之前,循环不能运行超过 n+m 次。
- 因为所有其他的工作都是常数,所以总的时间复杂度在矩阵维数之和中是线性的。
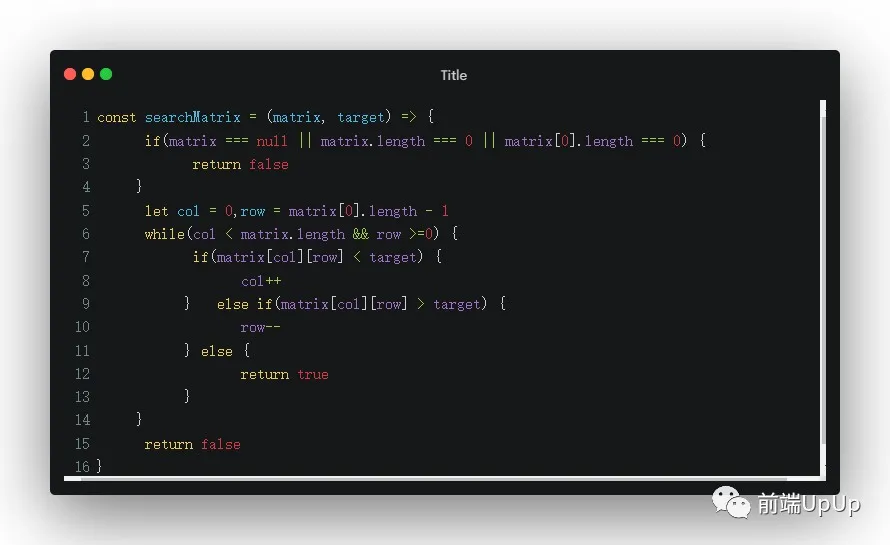
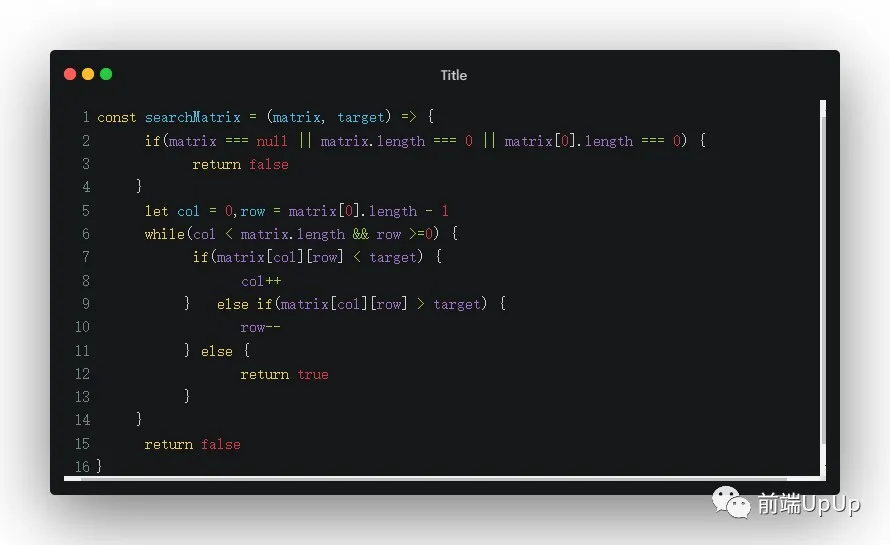
根据以上的伪代码,我们基本上就能解出这个题目👇
二位矩阵求值
这样子的解法,简单且容易理解,其实这并不是真正意义上的二分,只是根据数据的特殊性,使用特定的搜索方式完成对矩阵的查找。
既然一维数组查某个值时,我们可以将复杂度降为log级别的时间复杂度,那么在二维的情况下,我们是不是也可以这么考虑呢?
这个思路,可以借鉴一下👇
- 我们可以迭代矩阵对角线,二分搜索这些行和列,对它们进行切片。
- 在对角线上迭代,二分搜索行和列,知道对角线上的迭代元素用完为止(这个时候,就可以放回true或者是false)
说得更加简单一些,二分查找的思想是沿着对角线,行查找一下,列查找一下。
可以借鉴一下代码,就会明白如何利用矩阵的对角线去分治。
二位矩阵求值
代码点这里☑️
理清楚分治法思路,对它的特征有了一定的了解,明白何如利用它解决实际的问题,那或许这就是这篇文章的意义所在吧~
题目汇总
题目不多,但是对于基本的入门分治法,应该还是不错的选择👇
- 最大子序和
- 连续数列
- 切分数组