我们今天的面试题是这样的...
题目
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
示例:
- MinStack minStack = new MinStack();
- minStack.push(-2);
- minStack.push(0);
- minStack.push(-3);
- minStack.min(); --> 返回 -3.
- minStack.pop();
- minStack.top(); --> 返回 0.
- minStack.min(); --> 返回 -2.
- LeetCode 地址:leetcode-cn.com/problems/ba…
思考
首先来说这道题目本身很好理解,它的实现难点在于以下两个方面:
- 当我们进行 pop(移除栈顶元素)操作时如果删除的是当前最小值,那么我们如何寻找下一个最小值?
- 要保证调用 min、push 及 pop 的时间复杂度都是 O(1)。
也就是说,在我们执行了 pop 时如果移除的栈中最小的值,那么如何寻找栈中的下一个最小元素?并且要保证操作的时间复杂度为 O(1)。这个时间复杂度制约了我们在移除了最小值之后不能通过遍历查找下一个最小值,所以这就成为了这道题的难点。
比如当我们移除以下栈顶元素值:
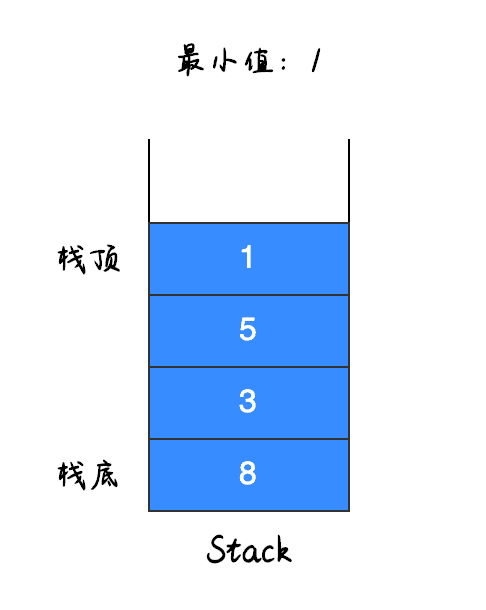
因为最小值就是 1,因此在移除之后最小值也被移除了,如下图所示:
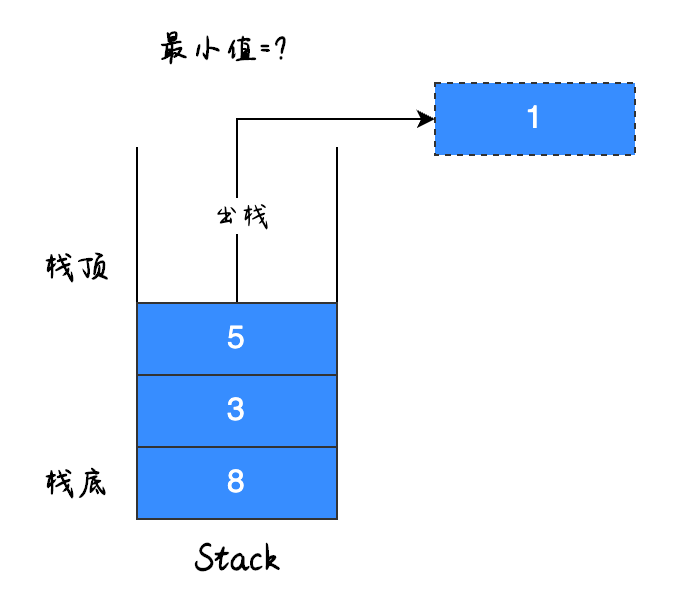
那么接下来,让我们一起思考 3 分钟,想一想应该如何处理这个问题~
解题思路
其实我们可以在每次入栈时,判断当前元素是否小于最小值,如果小于则将原最小值和最新的最小值相继入栈,这样在调用 pop 时即使移除的是最小值,我们也能通过获取下一个元素得到一个新的最小值,执行流程如下所示。
操作步骤1
入栈第一个元素,因为是第一个元素,因此最小值就是此元素的值。
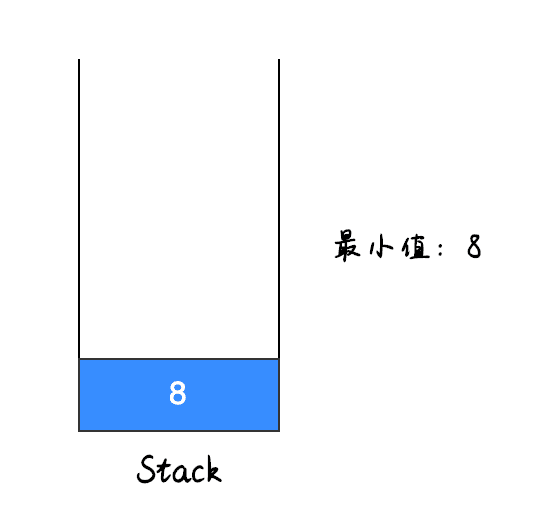
操作步骤2
入栈第二个元素,如下图所示:
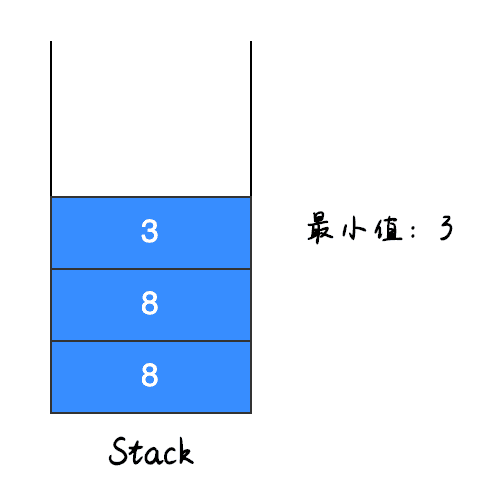
因为入栈的元素 3 比 8 小,所以先将栈中的原最小值 8 存入栈中,再将 3 入栈。
操作步骤3
入栈第三个元素,如下图所示:
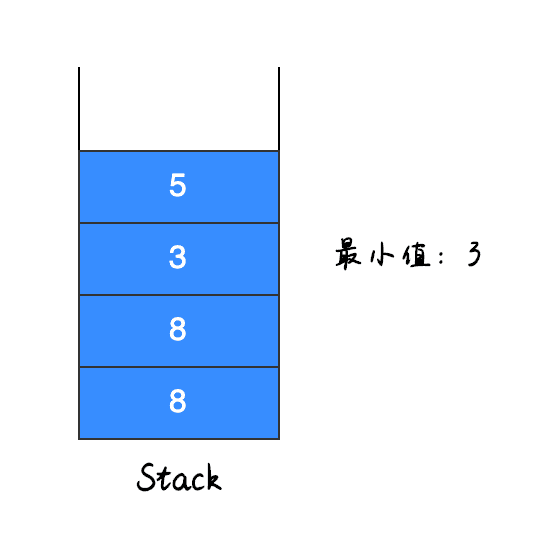
因为入栈元素 5 大于 3,因此栈中的最小值不变,直接将元素 5 入栈。
操作步骤4
继续入栈,如下图所示:
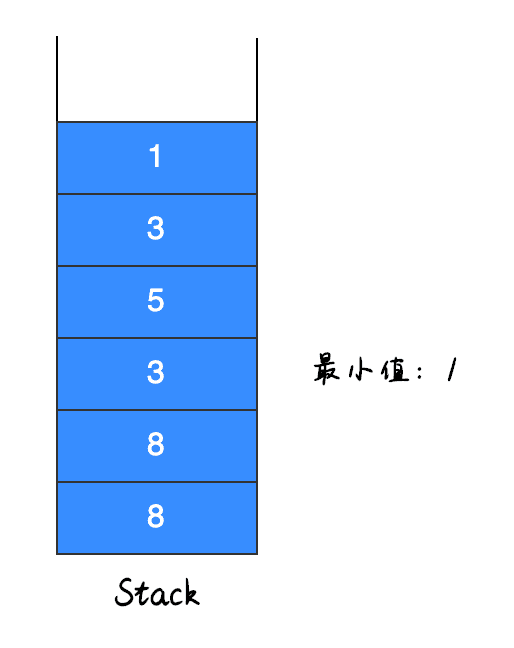
入栈元素 1 小于 3,因此先将原最小值 3 入栈,再将 1 入栈,栈中的最小值更改为 1。
操作步骤5
执行出栈操作,如下图所示: [图片上传中...(image-f68dcf-1602769401330-6)]
元素 1 出栈,判断当前元素就是栈的最小值,因此将栈顶元素 3 设置为最小值,并移除元素 3,如下图所示:
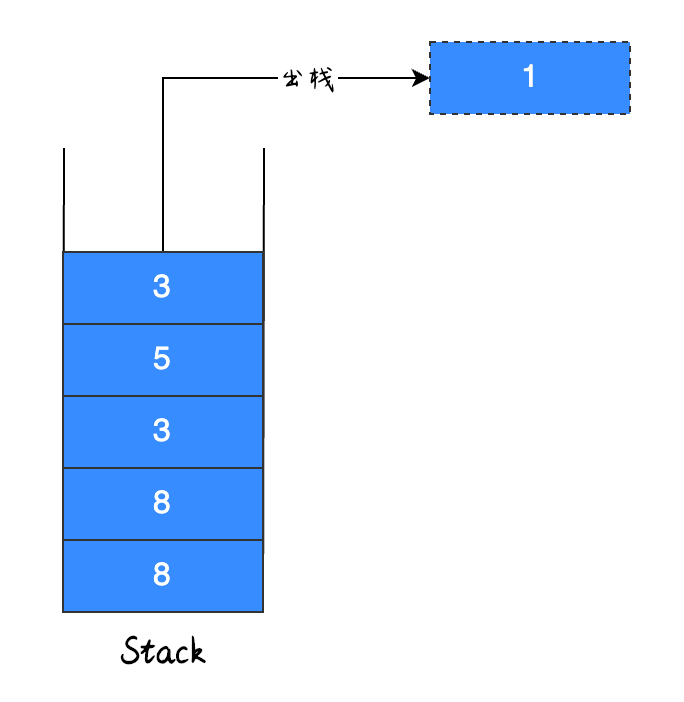
操作步骤6
继续出栈,如下图所示:
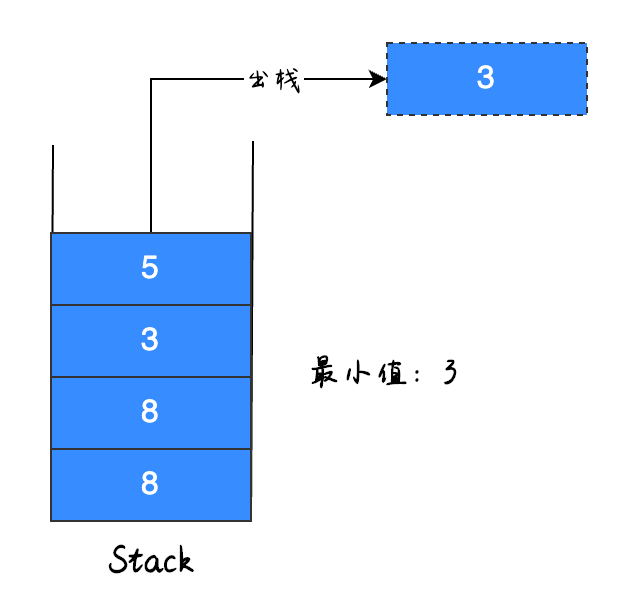
因为元素 5 不是当前最小值,因此直接出栈。
操作步骤7
继续出栈,如下图所示:
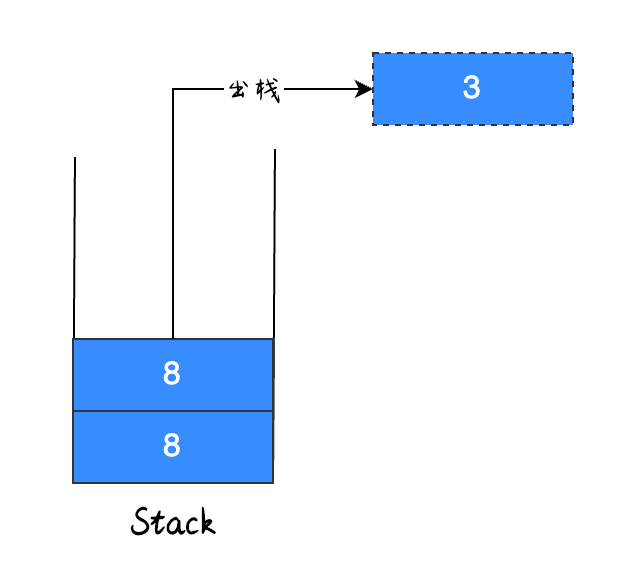
因为出栈元素 3 为最小值,因此继续将最小值设置为栈顶元素 8,并将栈顶元素出栈,如下图所示:
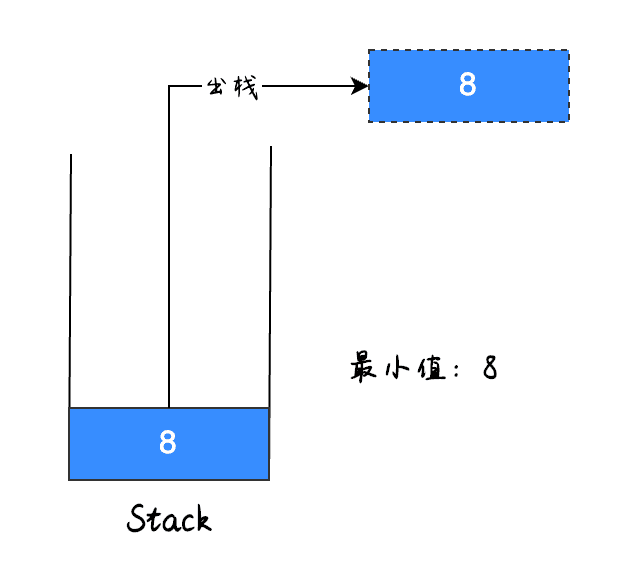
这样就剩下最后一个元素了,最后一个元素出栈之后就成空栈了,整个流程就执行完了。
实现代码1
接下来我们将上面的思路用代码实现一下,我们用数组实现的栈来实现相关的功能,代码如下:
- class MinStack {
- private int[] data; // 栈数据
- private int maxSize; // 最大长度
- private int top; // 栈顶指针(下标)
- private int min; // 最小值
- // 构造函数
- public MinStack() {
- // 设置默认值
- maxSize = 10000;
- data = new int[maxSize];
- top = -1;
- min = Integer.MAX_VALUE;
- }
- // 入栈(添加元素)
- public void push(int x) {
- if (min >= x) {
- // 遇到了更小的值,记录原最小值(入栈)
- data[++top] = min;
- min = x;
- }
- // 当前值入栈
- data[++top] = x;
- }
- // 出栈(移除栈顶元素)
- public void pop() {
- if (min == data[top]) {
- min = data[--top]; // 拿到原最小值,并(将原最小值)出栈
- }
- --top; // 出栈
- }
- // 查找栈顶元素
- public int top() {
- return data[top];
- }
- // 查询最小值
- public int min() {
- return min;
- }
- }
上述代码在 LeetCode 的执行结果如下:
可以看出性能还是很高的,超越了 99.92% 的用户,内存消耗也不大。它的核心代码在 push 方法内,先将原最小值和最新最小值相继入栈,在 pop 出栈时判断出栈元素是否为最小值,如果是最小值则将当前最小值指向栈顶元素并将栈顶元素出栈,这样就得到了下一个新的最小值了。
实现代码2
如果我们不想使用数组的自定义栈来实现,还可以使用 Java 中自带的栈 Stack 来实现此功能,代码如下:
- class MinStack {
- private Stack<Integer> stack = new Stack<>();
- private int min = Integer.MAX_VALUE;
- public MinStack() { }
- // 入栈(添加元素)
- public void push(int x) {
- if (x <= min) {
- // 遇到了更小的值,记录原最小值(入栈)
- stack.push(min);
- min = x;
- }
- stack.push(x);
- }
- // 出栈(移除栈顶元素)
- public void pop() {
- if (stack.pop() == min) {
- min = stack.pop(); // 取出原最小值
- }
- }
- // 查找栈顶元素
- public int top() {
- return stack.peek();
- }
- // 查询最小值
- public int min() {
- return min;
- }
- }
上述代码在 LeetCode 的执行结果如下:
从结果可以看出,使用 Java 中自带的栈的性能不如自定义数组的栈,但代码还是通过了测试。这种实现方式的优点就是代码比较简单,可以利用了 Java 自身的 API 来完成了最小值的查找。
这种实现代码的方式(使用 Java API),在刷题或者实际面试中如果没有特殊说明是可以直接用的。
总结
本文我们通过两种方式:自定义数组栈和 Java API 中的 Stack 来实现了栈中最小值的功能,保证了在调用栈的 min、push 及 pop 方法时的时间复杂度都是 O(1)。两种实现方式的代码虽然略不相同,但实现思路都是一样的,都是在元素入栈时判断当前元素是否小于最小元素,如果小于最小元素则先将原最小值入栈,再将当前最小元素入栈,这样当调用 pop 方法时,即使移除的是最小值,只需要将下一个元素取出即为新的最小值了,这样就可以实现调用 min、push 及 pop 方法时的时间复杂度都是 O(1) 了。