异常检测可以作为异常值分析的一项统计任务来处理。但是如果我们开发一个机器学习模型,它可以像往常一样自动化,可以节省很多时间。
异常检测有很多用例。信用卡欺诈检测、故障机器检测或基于异常特征的硬件系统检测、基于医疗记录的疾病检测都是很好的例子。还有更多的用例。异常检测的应用只会越来越多。
在本文中,我将解释在Python中从头开始开发异常检测算法的过程。
公式和过程
与我之前解释过的其他机器学习算法相比,这要简单得多。该算法将使用均值和方差来计算每个训练数据的概率。
如果一个训练实例的概率很高,这是正常的。如果某个训练实例的概率很低,那就是一个异常的例子。对于不同的训练集,高概率和低概率的定义是不同的。我们以后再讨论。
如果我要解释异常检测的工作过程,这很简单。
1. 使用以下公式计算平均值:
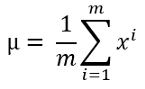
这里m是数据集的长度或训练数据的数量,而$x^i$是一个单独的训练例子。如果你有多个训练特征,大多数情况下都需要计算每个特征能的平均值。
2. 使用以下公式计算方差:
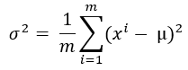
这里,mu是上一步计算的平均值。
3. 现在,用这个概率公式计算每个训练例子的概率。
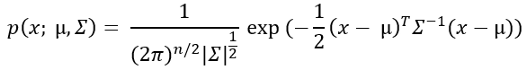
不要被这个公式中的求和符号弄糊涂了!这实际上是Sigma代表方差。
稍后我们将实现该算法时,你将看到它的样子。
4.我们现在需要找到概率的临界值。正如我前面提到的,如果一个训练例子的概率很低,那就是一个异常的例子。
低概率有多大?
这没有普遍的限制。我们需要为我们的训练数据集找出这个。
我们从步骤3中得到的输出中获取一系列概率值。对于每个概率,通过阈值的设置得到数据是否异常
然后计算一系列概率的精确度、召回率和f1分数。
精度可使用以下公式计算
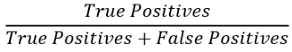
召回率的计算公式如下:
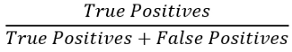
在这里,True positives(真正例)是指算法检测到一个异常的例子的数量,而它真实情况也是一个异常。
False Positives(假正例)当算法检测到一个异常的例子,但在实际情况中,它不是异常的,就会出现误报。
False Negative(假反例)是指算法检测到的一个例子不是异常的,但实际上它是一个异常的例子。
从上面的公式你可以看出,更高的精确度和更高的召回率总是好的,因为这意味着我们有更多的真正的正例。但同时,假正例和假反例起着至关重要的作用,正如你在公式中看到的那样。这需要一个平衡点。根据你的行业,你需要决定哪一个对你来说是可以忍受的。
一个好办法是取平均数。计算平均值有一个独特的公式。这就是f1分数。f1得分公式为:
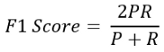
这里,P和R分别表示精确性和召回率。
根据f1分数,你需要选择你的阈值概率。
异常检测算法
我将使用Andrew Ng的机器学习课程的数据集,它具有两个训练特征。我没有在本文中使用真实的数据集,因为这个数据集非常适合学习。它只有两个特征。在任何真实的数据集中,都不可能只有两个特征。
首先,导入必要的包
- import pandas as pd
- import numpy as np
导入数据集。这是一个excel数据集。在这里,训练数据和交叉验证数据存储在单独的表中。所以,让我们把训练数据带来。
- df = pd.read_excel('ex8data1.xlsx', sheet_name='X', header=None)
- df.head()
让我们将第0列与第1列进行比较。
- plt.figure()
- plt.scatter(df[0], df[1])
- plt.show()
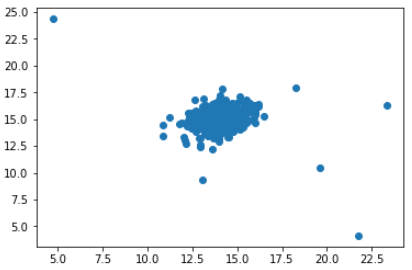
你可能通过看这张图知道哪些数据是异常的。
检查此数据集中有多少个训练示例:
- m = len(df)
计算每个特征的平均值。这里我们只有两个特征:0和1。
- s = np.sum(df, axis=0)
- mu = s/m
- mu
输出:
- 0 14.112226
- 1 14.997711
- dtype: float64
根据上面“公式和过程”部分中描述的公式,让我们计算方差:
- vr = np.sum((df - mu)**2, axis=0)
- variance = vr/m
- variance
输出:
- 0 1.832631
- 1 1.709745
- dtype: float64
现在把它做成对角线形状。正如我在概率公式后面的“公式和过程”一节中所解释的,求和符号实际上是方差
- var_dia = np.diag(variance)
- var_dia
输出:
- array([[1.83263141, 0. ],
- [0. , 1.70974533]])
计算概率:
- k = len(mu)
- X = df - mu
- p = 1/((2*np.pi)**(k/2)*(np.linalg.det(var_dia)**0.5))* np.exp(-0.5* np.sum(X @ np.linalg.pinv(var_dia) * X,axis=1))
- p
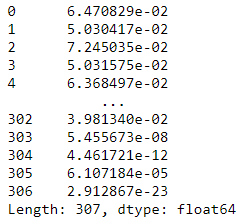
训练部分已经完成。
下一步是找出阈值概率。如果概率低于阈值概率,则示例数据为异常数据。但我们需要为我们的特殊情况找出那个阈值。
对于这一步,我们使用交叉验证数据和标签。
对于你的案例,你只需保留一部分原始数据以进行交叉验证。
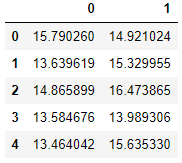
现在导入交叉验证数据和标签:
- cvx = pd.read_excel('ex8data1.xlsx', sheet_name='Xval', header=None)
- cvx.head()
标签如下:
- cvy = pd.read_excel('ex8data1.xlsx', sheet_name='y', header=None)
- cvy.head()

我将把'cvy'转换成NumPy数组,因为我喜欢使用数组。不过,数据帧也不错。
- y = np.array(cvy)
输出:
- # 数组的一部分
- array([[0],
- [0],
- [0],
- [0],
- [0],
- [0],
- [0],
- [0],
- [0],
这里,y值0表示这是一个正常的例子,y值1表示这是一个异常的例子。
现在,如何选择一个阈值?
我不想只检查概率表中的所有概率。这可能是不必要的。让我们再检查一下概率值。
- p.describe()
输出:
- count 3.070000e+02
- mean 5.905331e-02
- std 2.324461e-02
- min 1.181209e-23
- 25% 4.361075e-02
- 50% 6.510144e-02
- 75% 7.849532e-02
- max 8.986095e-02
- dtype: float64
如图所示,我们没有太多异常数据。所以,如果我们从75%的值开始,这应该是好的。但为了安全起见,我会从平均值开始。
因此,我们将从平均值和更低的概率范围。我们将检查这个范围内每个概率的f1分数。
首先,定义一个函数来计算真正例、假正例和假反例:
- def tpfpfn(ep):
- tp, fp, fn = 0, 0, 0
- for i in range(len(y)):
- if p[i] <= ep and y[i][0] == 1:
- tp += 1
- elif p[i] <= ep and y[i][0] == 0:
- fp += 1
- elif p[i] > ep and y[i][0] == 1:
- fn += 1
- return tp, fp, fn
列出低于或等于平均概率的概率。
- eps = [i for i in p if i <= p.mean()]
检查一下列表的长度
- len(eps)
输出:
- 133
根据前面讨论的公式定义一个计算f1分数的函数:
- def f1(ep):
- tp, fp, fn = tpfpfn(ep)
- prec = tp/(tp + fp)
- rec = tp/(tp + fn)
- f1 = 2*prec*rec/(prec + rec)
- return f1
所有函数都准备好了!
现在计算所有epsilon或我们之前选择的概率值范围的f1分数。
- f = []
- for i in eps:
- f.append(f1(i))
- f
输出:
- [0.14285714285714285,
- 0.14035087719298248,
- 0.1927710843373494,
- 0.1568627450980392,
- 0.208955223880597,
- 0.41379310344827586,
- 0.15517241379310345,
- 0.28571428571428575,
- 0.19444444444444445,
- 0.5217391304347826,
- 0.19718309859154928,
- 0.19753086419753085,
- 0.29268292682926833,
- 0.14545454545454545,
这是f分数表的一部分。长度应该是133。
f分数通常在0到1之间,其中f1得分越高越好。所以,我们需要从刚才计算的f分数列表中取f的最高分数。
现在,使用“argmax”函数来确定f分数值最大值的索引。
- np.array(f).argmax()
输出:
- 131
现在用这个索引来得到阈值概率。
- e = eps[131]
- e
输出:
- 6.107184445968581e-05
找出异常实例
我们有临界概率。我们可以从中找出我们训练数据的标签。
如果概率值小于或等于该阈值,则数据为异常数据,否则为正常数据。我们将正常数据和异常数据分别表示为0和1,
- label = []
- for i in range(len(df)):
- if p[i] <= e:
- label.append(1)
- else:
- label.append(0)
- label
输出:
- [0,
- 0,
- 0,
- 0,
- 0,
- 0,
- 0,
- 0,
- 0,
- 0,
这是标签列表的一部分。
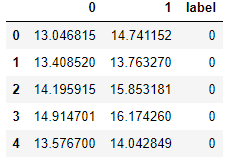
我将在上面的训练数据集中添加此计算标签:
- df['label'] = np.array(label)
- df.head()
我在标签为1的地方用红色绘制数据,在标签为0的地方用黑色绘制。以下是结果。
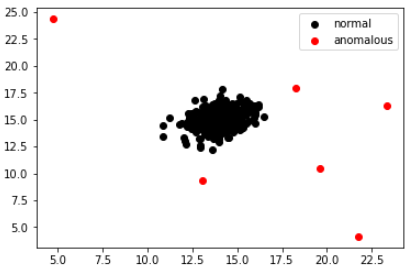
有道理吗?
是的,对吧?红色的数据明显异常。
结论
我试图一步一步地解释开发异常检测算法的过程,我希望这是可以理解的。如果你仅仅通过阅读就无法理解,建议你运行每一段代码。那就很清楚了。






































