前言
递归是一种非常重要的算法思想,无论你是前端开发,还是后端开发,都需要掌握它。在日常工作中,统计文件夹大小,解析xml文件等等,都需要用到递归算法。它太基础太重要了,这也是为什么面试的时候,面试官经常让我们手写递归算法。本文呢,将跟大家一起学习递归算法~
- 什么是递归?
- 递归的特点
- 递归与栈的关系
- 递归应用场景
- 递归解题思路
- leetcode案例分析
- 递归可能存在的问题以及解决方案
什么是递归?
递归,在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。简单来说,递归表现为函数调用函数本身。在知乎看到一个比喻递归的例子,个人觉得非常形象,大家看一下:
❝递归最恰当的比喻,就是查词典。我们使用的词典,本身就是递归,为了解释一个词,需要使用更多的词。当你查一个词,发现这个词的解释中某个词仍然不懂,于是你开始查这第二个词,可惜,第二个词里仍然有不懂的词,于是查第三个词,这样查下去,直到有一个词的解释是你完全能看懂的,那么递归走到了尽头,然后你开始后退,逐个明白之前查过的每一个词,最终,你明白了最开始那个词的意思。❞
来试试水,看一个递归的代码例子吧,如下:
- public int sum(int n) {
- if (n <= 1) {
- return 1;
- }
- return sum(n - 1) + n;
- }
递归的特点
实际上,递归有两个显著的特征,终止条件和自身调用:
- 自身调用:原问题可以分解为子问题,子问题和原问题的求解方法是一致的,即都是调用自身的同一个函数。
- 终止条件:递归必须有一个终止的条件,即不能无限循环地调用本身。
结合以上demo代码例子,看下递归的特点:
递归与栈的关系
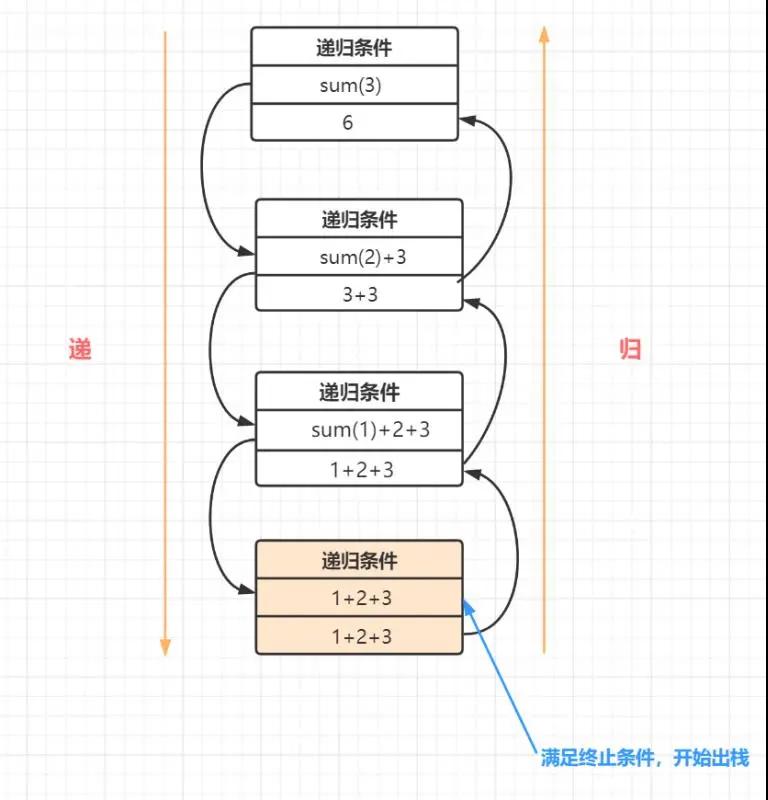
其实,递归的过程,可以理解为出入栈的过程的,这个比喻呢,只是为了方便读者朋友更好理解递归哈。以上代码例子计算sum(n=3)的出入栈图如下:
为了更容易理解一些,我们来看一下 函数sum(n=5)的递归执行过程,如下:
- 计算sum(5)时,先sum(5)入栈,然后原问题sum(5)拆分为子问题sum(4),再入栈,直到终止条件sum(n=1)=1,就开始出栈。
- sum(1)出栈后,sum(2)开始出栈,接着sum(3)。
- 最后呢,sum(1)就是后进先出,sum(5)是先进后出,因此递归过程可以理解为栈出入过程啦~
递归的经典应用场景
哪些问题我们可以考虑使用递归来解决呢?即递归的应用场景一般有哪些呢?
- 阶乘问题
- 二叉树深度
- 汉诺塔问题
- 斐波那契数列
- 快速排序、归并排序(分治算法体现递归)
- 遍历文件,解析xml文件
递归解题思路
解决递归问题一般就三步曲,分别是:
- 第一步,定义函数功能
- 第二步,寻找递归终止条件
- 第二步,递推函数的等价关系式
这个递归解题三板斧理解起来有点抽象,我们拿阶乘递归例子来喵喵吧~
1.定义函数功能
定义函数功能,就是说,你这个函数是干嘛的,做什么事情,换句话说,你要知道递归原问题是什么呀?比如你需要解决阶乘问题,定义的函数功能就是n的阶乘,如下:
- //n的阶乘(n为大于0的自然数)
- int factorial (int n){
- }
2.寻找递归终止条件
递归的一个典型特征就是必须有一个终止的条件,即不能无限循环地调用本身。所以,用递归思路去解决问题的时候,就需要寻找递归终止条件是什么。比如阶乘问题,当n=1的时候,不用再往下递归了,可以跳出循环啦,n=1就可以作为递归的终止条件,如下:
- //n的阶乘(n为大于0的自然数)
- int factorial (int n){
- if(n==1){
- return 1;
- }
- }
3.递推函数的等价关系式
递归的「本义」,就是原问题可以拆为同类且更容易解决的子问题,即「原问题和子问题都可以用同一个函数关系表示。递推函数的等价关系式,这个步骤就等价于寻找原问题与子问题的关系,如何用一个公式把这个函数表达清楚」。阶乘的公式就可以表示为 f(n) = n * f(n-1), 因此,阶乘的递归程序代码就可以写成这样,如下:
- int factorial (int n){
- if(n==1){
- return 1;
- }
- return n * factorial(n-1);
- }
「注意啦」,不是所有递推函数的等价关系都像阶乘这么简单,一下子就能推导出来。需要我们多接触,多积累,多思考,多练习递归题目滴~
leetcode案例分析
来分析一道leetcode递归的经典题目吧~
❝原题链接在这里哈:https://leetcode-cn.com/problems/invert-binary-tree/❞
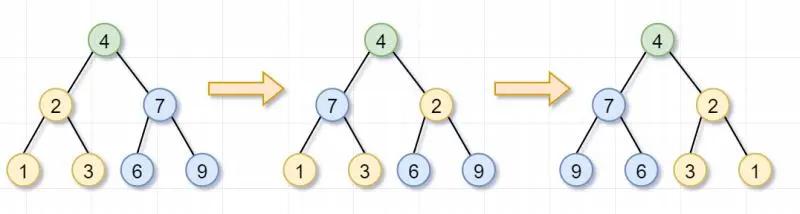
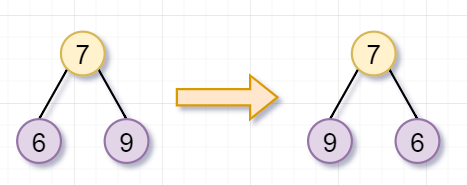
「题目:」 翻转一棵二叉树。
输入:
- 4
- / \
- 2 7
- / \ / \
- 1 3 6 9
输出:
- 4
- / \
- 7 2
- / \ / \
- 9 6 3 1
我们按照以上递归解题的三板斧来:
「1. 定义函数功能」
函数功能(即这个递归原问题是),给出一颗树,然后翻转它,所以,函数可以定义为:
- //翻转一颗二叉树
- public TreeNode invertTree(TreeNode root) {
- }
- /**
- * Definition for a binary tree node.
- * public class TreeNode {
- * int val;
- * TreeNode left;
- * TreeNode right;
- * TreeNode(int x) { val = x; }
- * }
- */
「2.寻找递归终止条件」
这棵树什么时候不用翻转呢?当然是当前节点为null或者当前节点为叶子节点的时候啦。因此,加上终止条件就是:
- //翻转一颗二叉树
- public TreeNode invertTree(TreeNode root) {
- if(root==null || (root.left ==null && root.right ==null)){
- return root;
- }
- }
「3. 递推函数的等价关系式」
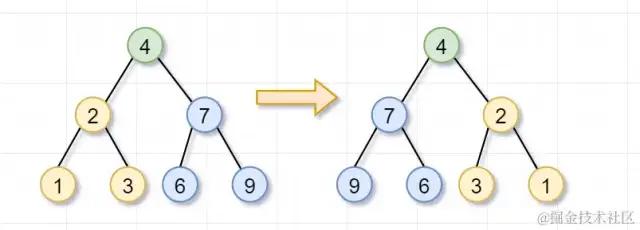
原问题之你要翻转一颗树,是不是可以拆分为子问题,分别翻转它的左子树和右子树?子问题之翻转它的左子树,是不是又可以拆分为,翻转它左子树的左子树以及它左子树的右子树?然后一直翻转到叶子节点为止。嗯,看图理解一下咯~
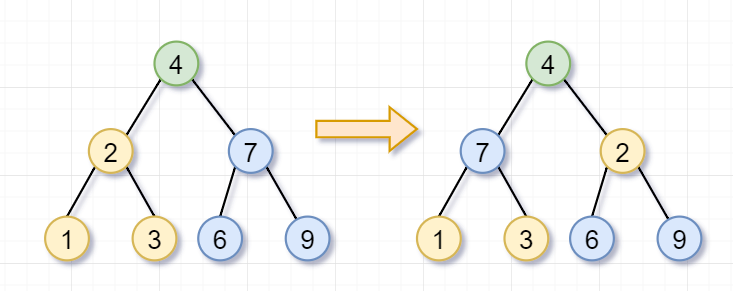
首先,你要翻转根节点为4的树,就需要「翻转它的左子树(根节点为2)和右子树(根节点为7)」。这就是递归的「递」的过程啦
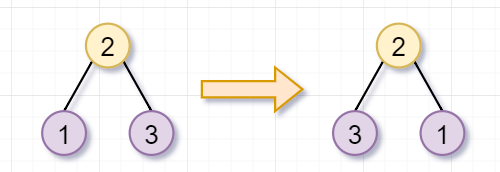
然后呢,根节点为2的树,不是叶子节点,你需要继续「翻转它的左子树(根节点为1)和右子树(根节点为3)」。因为节点1和3都是「叶子节点」了,所以就返回啦。这也是递归的「递」的过程~
同理,根节点为7的树,也不是叶子节点,你需要翻转「它的左子树(根节点为6)和右子树(根节点为9)」。因为节点6和9都是叶子节点了,所以也返回啦。
左子树(根节点为2)和右子树(根节点为7)都被翻转完后,这几个步骤就「归来」,即递归的归过程,翻转树的任务就完成了~
显然,「递推关系式」就是:
- invertTree(root)= invertTree(root.left) + invertTree(root.right);
于是,很容易可以得出以下代码:
- //翻转一颗二叉树
- public TreeNode invertTree(TreeNode root) {
- if(root==null || (root.left ==null && root.right ==null){
- return root;
- }
- //翻转左子树
- TreeNode left = invertTree(root.left);
- //翻转右子树
- TreeNode right= invertTree(root.right);
- }
这里代码有个地方需要注意,翻转完一棵树的左右子树,还要交换它左右子树的引用位置。
- root.left = right;
- root.right = left;
因此,leetcode这个递归经典题目的「终极解决代码」如下:
- class Solution {
- public TreeNode invertTree(TreeNode root) {
- if(root==null || (root.left ==null && root.right ==null)){
- return root;
- }
- //翻转左子树
- TreeNode left = invertTree(root.left);
- //翻转右子树
- TreeNode right= invertTree(root.right);
- //左右子树交换位置~
- root.left = right;
- root.right = left;
- return root;
- }
- }
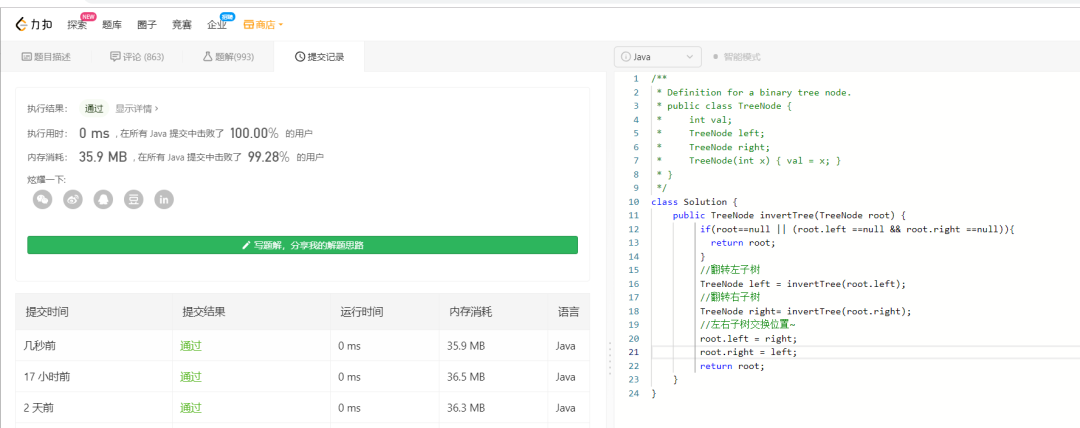
拿终极解决代码去leetcode提交一下,通过啦~
递归存在的问题
- 递归调用层级太多,导致栈溢出问题
- 递归重复计算,导致效率低下
栈溢出问题
- 每一次函数调用在内存栈中分配空间,而每个进程的栈容量是有限的。
- 当递归调用的层级太多时,就会超出栈的容量,从而导致调用栈溢出。
- 其实,我们在前面小节也讨论了,递归过程类似于出栈入栈,如果递归次数过多,栈的深度就需要越深,最后栈容量真的不够咯
「代码例子如下:」
- /**
- * 递归栈溢出测试
- */
- public class RecursionTest {
- public static void main(String[] args) {
- sum(50000);
- }
- private static int sum(int n) {
- if (n <= 1) {
- return 1;
- }
- return sum(n - 1) + n;
- }
- }
「运行结果:」
Exception in thread "main" java.lang.StackOverflowError at recursion.RecursionTest.sum(RecursionTest.java:13)
怎么解决这个栈溢出问题?首先需要「优化一下你的递归」,真的需要递归调用这么多次嘛?如果真的需要,先稍微「调大JVM的栈空间内存」,如果还是不行,那就需要弃用递归,「优化为其他方案」咯~
重复计算,导致程序效率低下
我们再来看一道经典的青蛙跳阶问题:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
绝大多数读者朋友,很容易就想到以下递归代码去解决:
- class Solution {
- public int numWays(int n) {
- if (n == 0){
- return 1;
- }
- if(n <= 2){
- return n;
- }
- return numWays(n-1) + numWays(n-2);
- }
- }
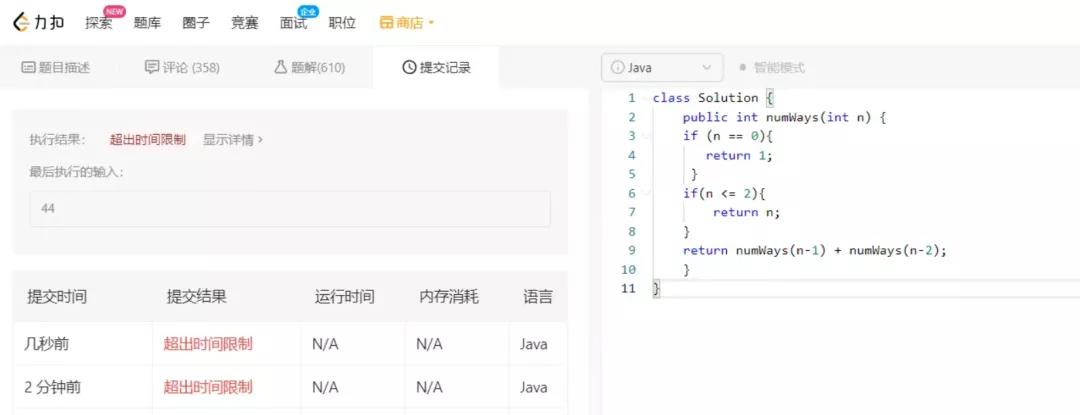
但是呢,去leetcode提交一下,就有问题啦,超出时间限制了
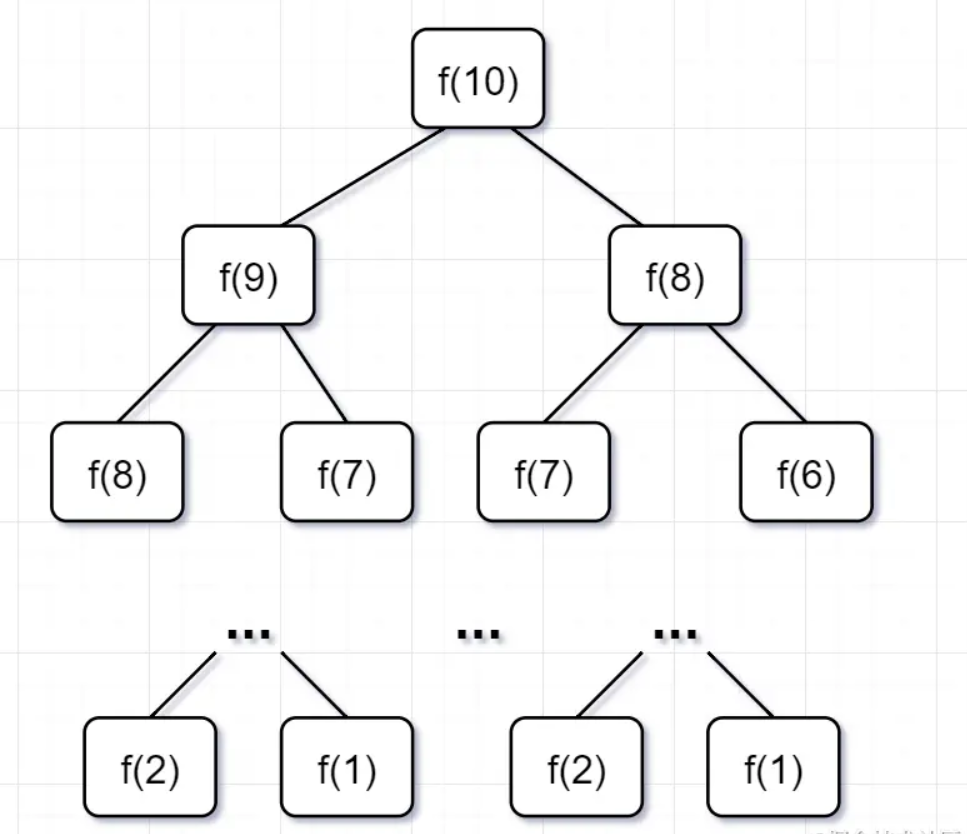
为什么超时了呢?递归耗时在哪里呢?先画出「递归树」看看:
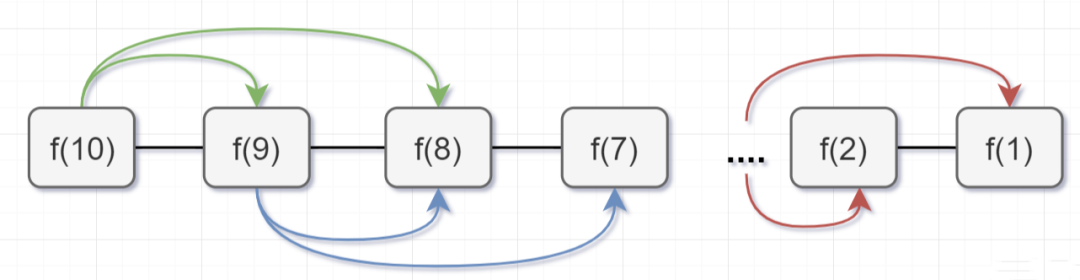
要计算原问题 f(10),就需要先计算出子问题 f(9) 和 f(8)
然后要计算 f(9),又要先算出子问题 f(8) 和 f(7),以此类推。
一直到 f(2) 和 f(1),递归树才终止。
我们先来看看这个递归的时间复杂度吧,「递归时间复杂度 = 解决一个子问题时间*子问题个数」
- 一个子问题时间 = f(n-1)+f(n-2),也就是一个加法的操作,所以复杂度是「O(1)」;
- 问题个数 = 递归树节点的总数,递归树的总结点 = 2^n-1,所以是复杂度「O(2^n)」。
因此,青蛙跳阶,递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n),就是指数级别的,爆炸增长的,「如果n比较大的话,超时很正常的了」。
回过头来,你仔细观察这颗递归树,你会发现存在「大量重复计算」,比如f(8)被计算了两次,f(7)被重复计算了3次...所以这个递归算法低效的原因,就是存在大量的重复计算!
「那么,怎么解决这个问题呢?」
既然存在大量重复计算,那么我们可以先把计算好的答案存下来,即造一个备忘录,等到下次需要的话,先去「备忘录」查一下,如果有,就直接取就好了,备忘录没有才再计算,那就可以省去重新重复计算的耗时啦!这就是「带备忘录的解法」
我们来看一下「带备忘录的递归解法」吧~
一般使用一个数组或者一个哈希map充当这个「备忘录」。
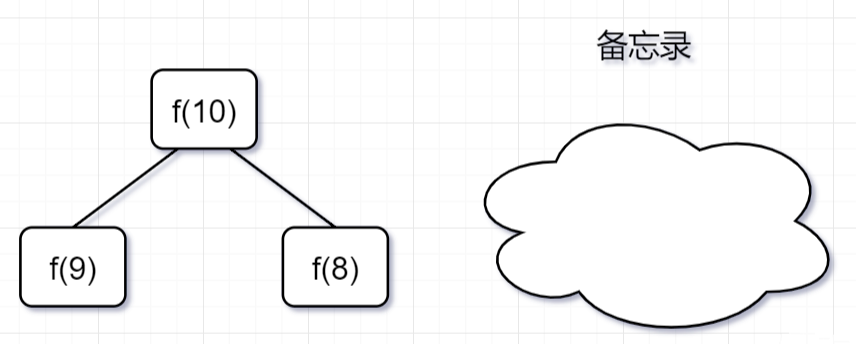
假设f(10)求解加上「备忘录」,我们再来画一下递归树:
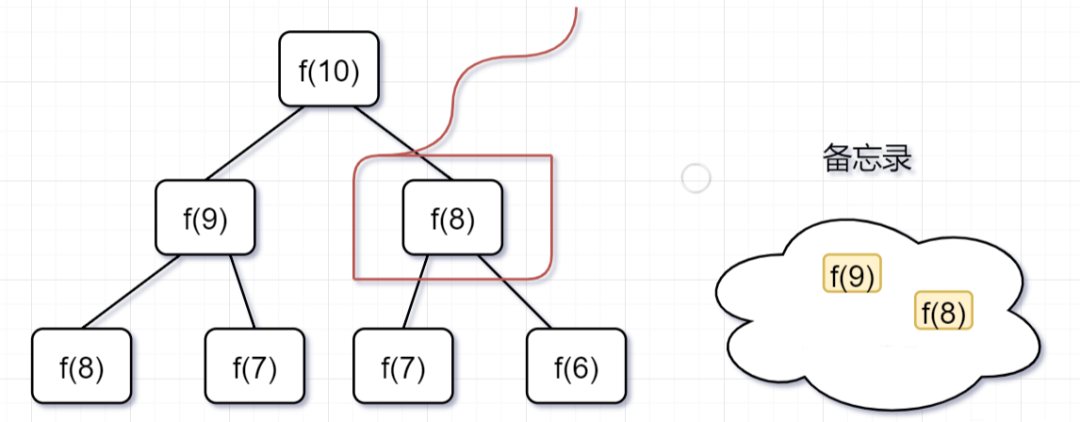
「第一步」,f(10)= f(9) + f(8),f(9) 和f(8)都需要计算出来,然后再加到备忘录中,如下:
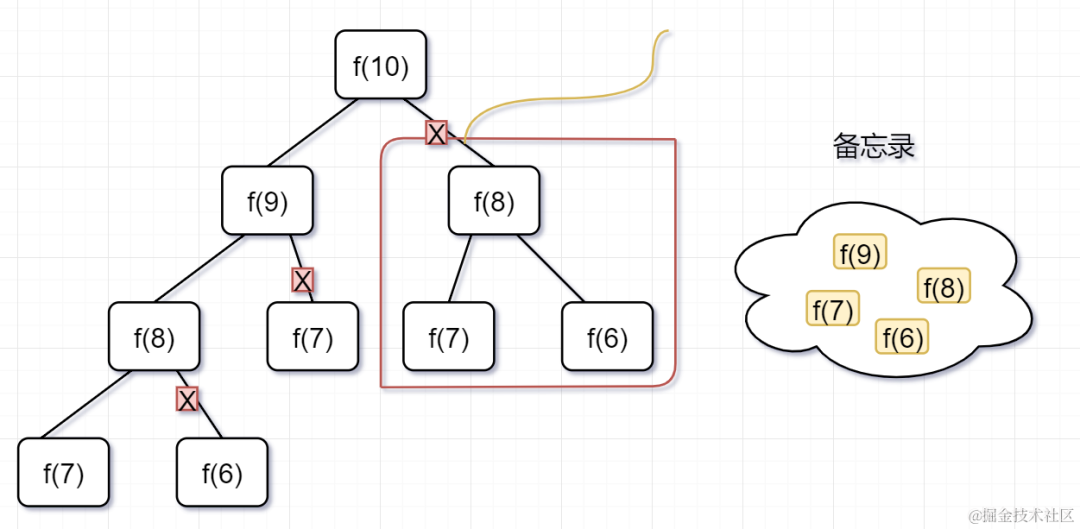
「第二步,」 f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中~
「第三步,」 f(8) = f(7)+ f(6),发现f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉。
所以呢,用了备忘录递归算法,递归树变成光秃秃的树干咯,如下:
带「备忘录」的递归算法,子问题个数=树节点数=n,解决一个子问题还是O(1),所以「带「备忘录」的递归算法的时间复杂度是O(n)」。接下来呢,我们用带「备忘录」的递归算法去撸代码,解决这个青蛙跳阶问题的超时问题咯~,代码如下:
- public class Solution {
- //使用哈希map,充当备忘录的作用
- Map<Integer, Integer> tempMap = new HashMap();
- public int numWays(int n) {
- // n = 0 也算1种
- if (n == 0) {
- return 1;
- }
- if (n <= 2) {
- return n;
- }
- //先判断有没计算过,即看看备忘录有没有
- if (tempMap.containsKey(n)) {
- //备忘录有,即计算过,直接返回
- return tempMap.get(n);
- } else {
- // 备忘录没有,即没有计算过,执行递归计算,并且把结果保存到备忘录map中,对1000000007取余(这个是leetcode题目规定的)
- tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);
- return tempMap.get(n);
- }
- }
- }
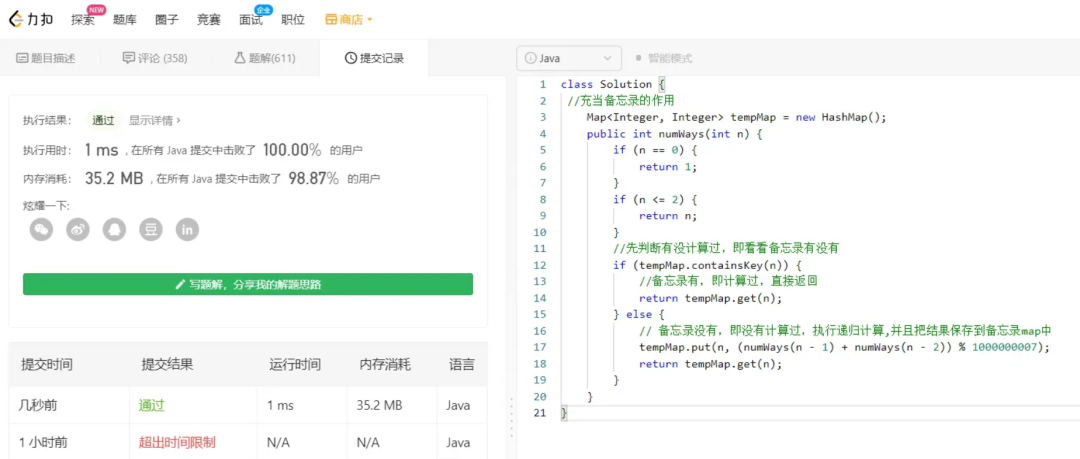
去leetcode提交一下,如图,稳了:
还有没有其他方案解决这个问题呢?只有「带备忘录的递归解法」?其实吧,还可以用「动态规划」去解决
本文转载自微信公众号「 捡田螺的小男孩」,可以通过以下二维码关注。转载本文请联系 捡田螺的小男孩公众号。