快速介绍10种基本图形算法以及示例和可视化
在现实世界中,例如社交媒体网络,网页和链接以及GPS中的位置和路线,图形已经成为一种强大的建模和捕获数据的手段。 如果您有一组相互关联的对象,则可以使用图形来表示它们。
在本文中,我将简要说明10种基本图形算法,这些算法对于分析及其应用非常有用。
首先,让我们介绍一个图表。
什么是图?
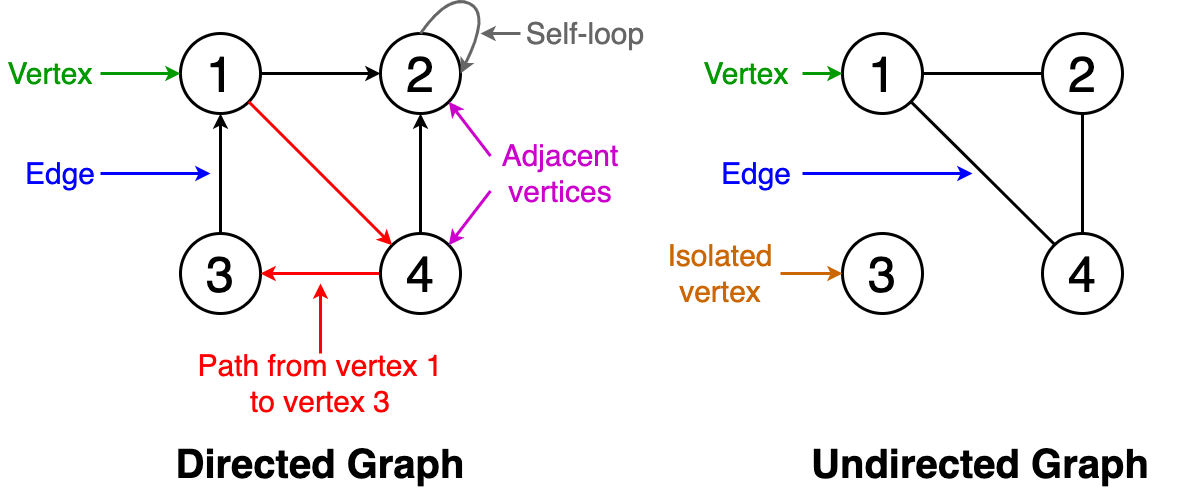
一个图由一组有限的顶点或节点以及一组连接这些顶点的边组成。 如果两个顶点通过同一边彼此连接,则它们称为相邻顶点。
下面给出一些与图有关的基本定义。 您可以参考图1的示例。
- 顺序:图形中的顶点数
- 大小:图形中的边数
- 顶点度:入射到顶点的边数
- 孤立的顶点:未连接到图中任何其他顶点的顶点
- 自环:从顶点到自身的边
- 有向图:所有边都有一个方向的图,该方向指示什么是起始顶点,什么是终止顶点
- 无向图:具有没有方向的边的图
- 加权图:图的边缘具有权重
- 未加权图形:图形的边缘没有权重
1.广度优先搜索
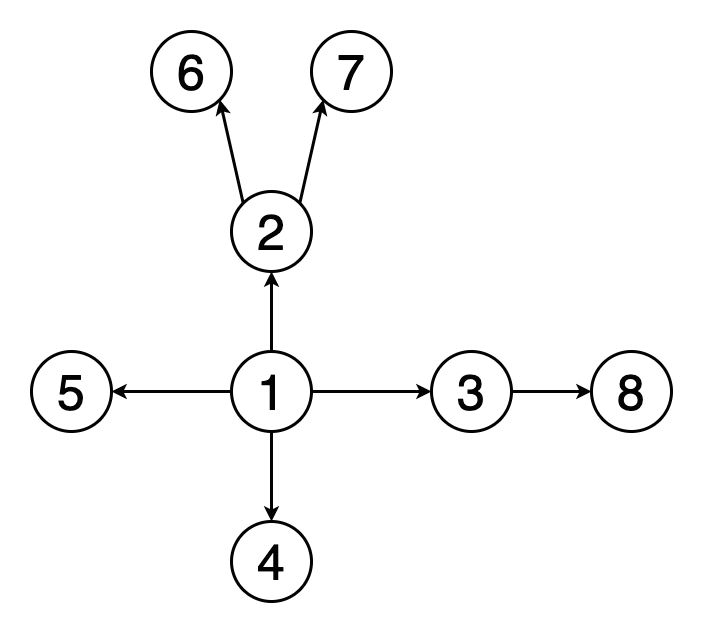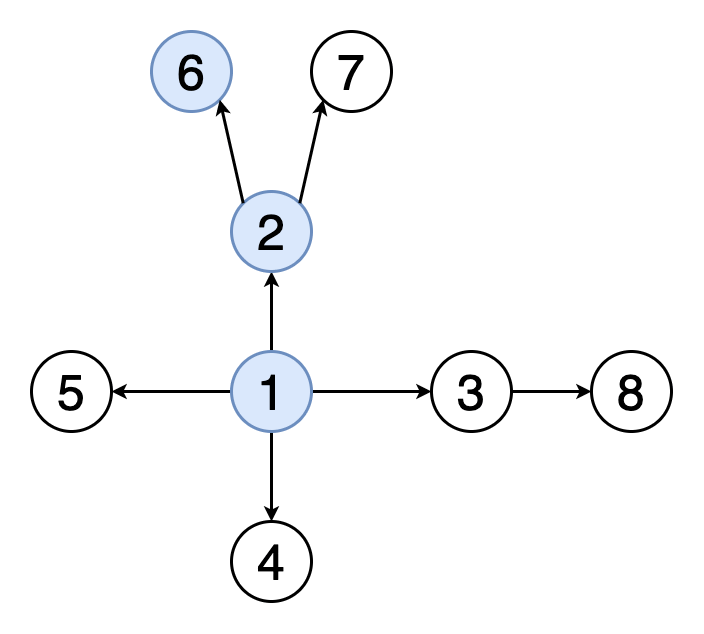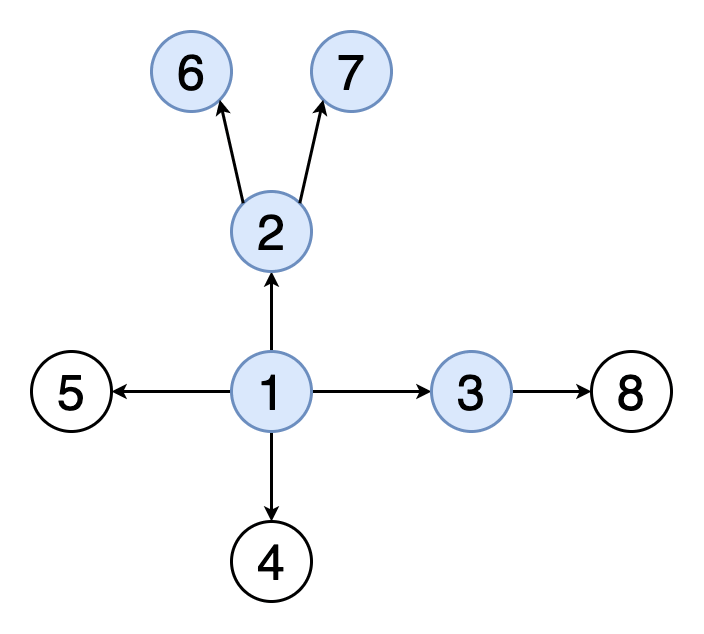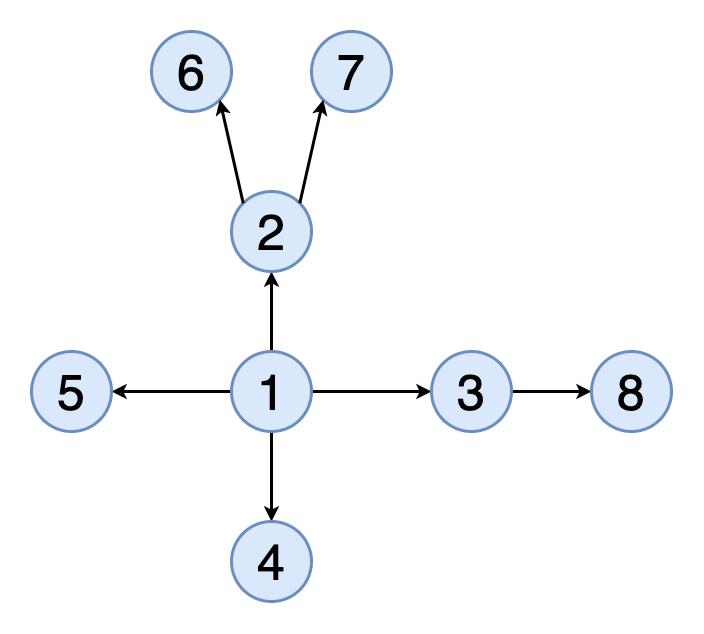
遍历或搜索是可以在图形上执行的基本操作之一。 在广度优先搜索(BFS)中,我们从一个特定的顶点开始,并在当前深度探索其所有邻居,然后再进入下一级的顶点。 与树不同,图可以包含循环(第一个顶点和最后一个顶点相同的路径)。 因此,我们必须跟踪访问的顶点。 在实现BFS时,我们使用队列数据结构。
图2表示示例图的BFS遍历的动画。 注意如何发现顶点(黄色)并访问顶点(红色)。
应用领域
- 用于确定最短路径和最小生成树。
- 搜索引擎搜寻器用来构建网页索引。
- 用于在社交网络上搜索。
- 用于查找对等网络(例如BitTorrent)中的可用邻居节点。
2.深度优先搜索
在深度优先搜索(DFS)中,我们从特定的顶点开始,并在回溯(回溯)之前沿每个分支进行尽可能的探索。 在DFS中,我们还必须跟踪访问的顶点。 在实现DFS时,我们使用堆栈数据结构来支持回溯。
图3表示与图2相同的示例图的DFS遍历的动画。请注意,它如何遍历深度和回溯。
应用领域
- 用于查找两个顶点之间的路径。
- 用于检测图中的周期。
- 用于拓扑排序。
- 用于解决只有一种解决方案(例如迷宫)的难题
3.最短路径
从一个顶点到另一个顶点的最短路径是图形中的一条路径,因此应移动的边的权重之和最小。
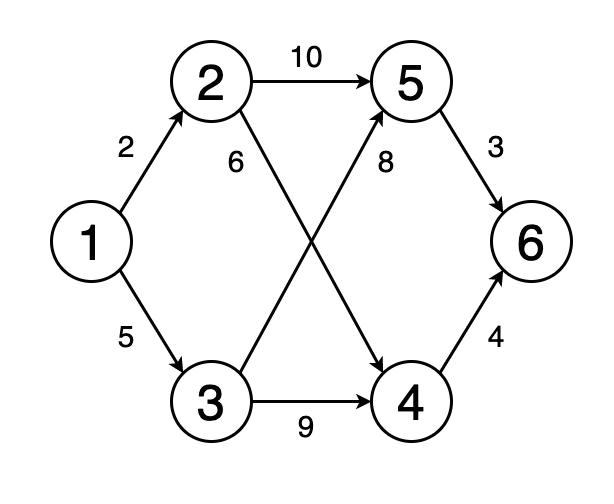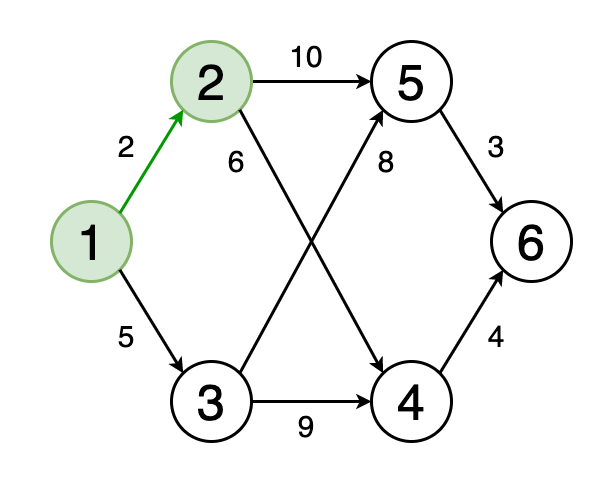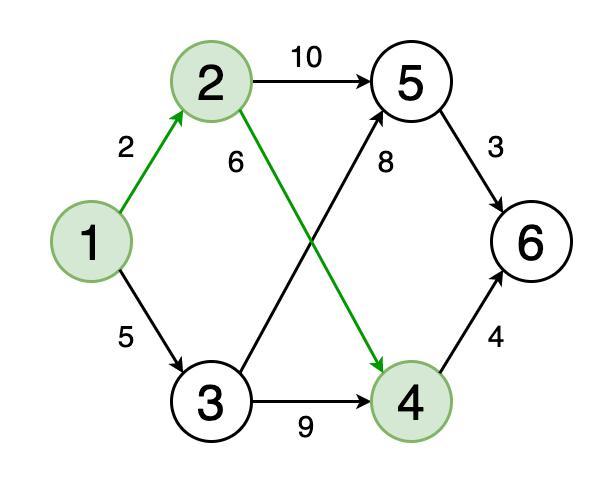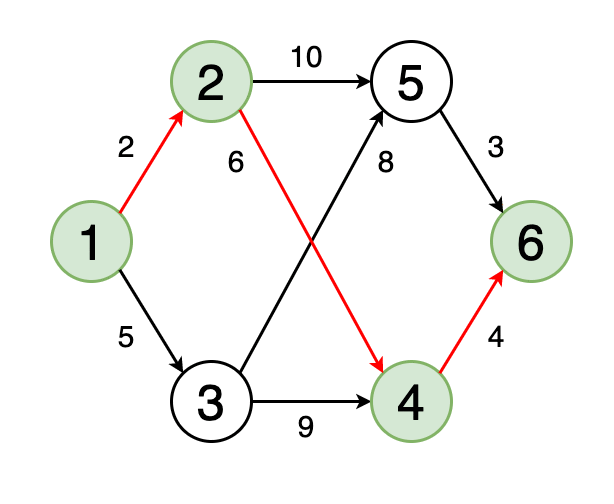
图4显示了一个动画,其中确定了图形中从顶点1到顶点6的最短路径。
演算法
- Dijkstra最短路径算法
- Bellman–Ford算法
应用领域
- 用于在Google地图或Apple地图等地图软件中查找从一个位置到另一个位置的路线。
- 用于网络中以解决最小延迟路径问题。
- 用于抽象机器中,以通过在不同状态之间进行转换来确定达到某个目标状态的选择(例如,可用于确定赢得一场比赛的最小可能次数)。
4.循环检测
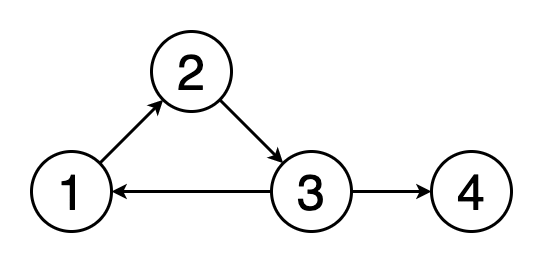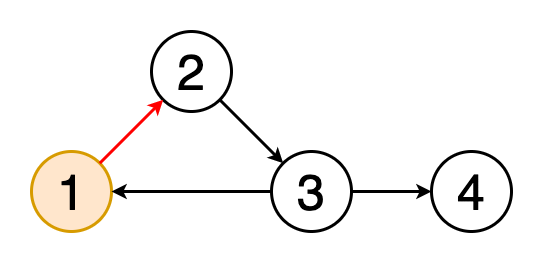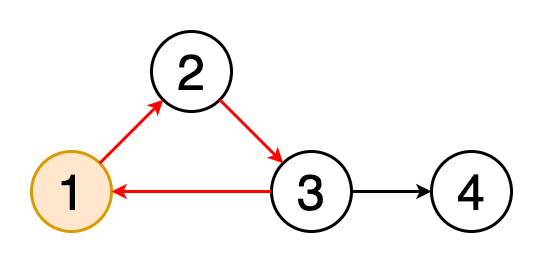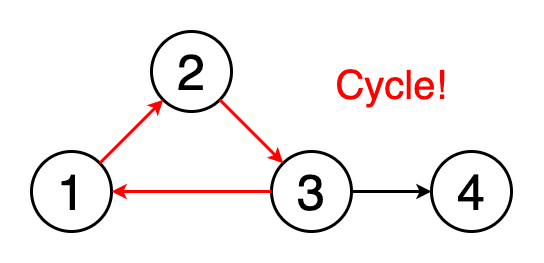
循环是图形中的第一个顶点和最后一个顶点相同的路径。 如果我们从一个顶点开始,沿着一条路径行进,然后在起始顶点处结束,那么这条路径就是一个循环。 循环检测是检测这些循环的过程。 图5显示了遍历一个循环的动画。
演算法
- 弗洛伊德循环检测算法
- 布伦特算法
应用领域
- 用于基于分布式消息的算法。
- 用于在群集上使用分布式处理系统处理大规模图形。
- 用于检测并发系统中的死锁。
- 在加密应用程序中用于确定消息的密钥,该密钥可以将该消息映射到相同的加密值。
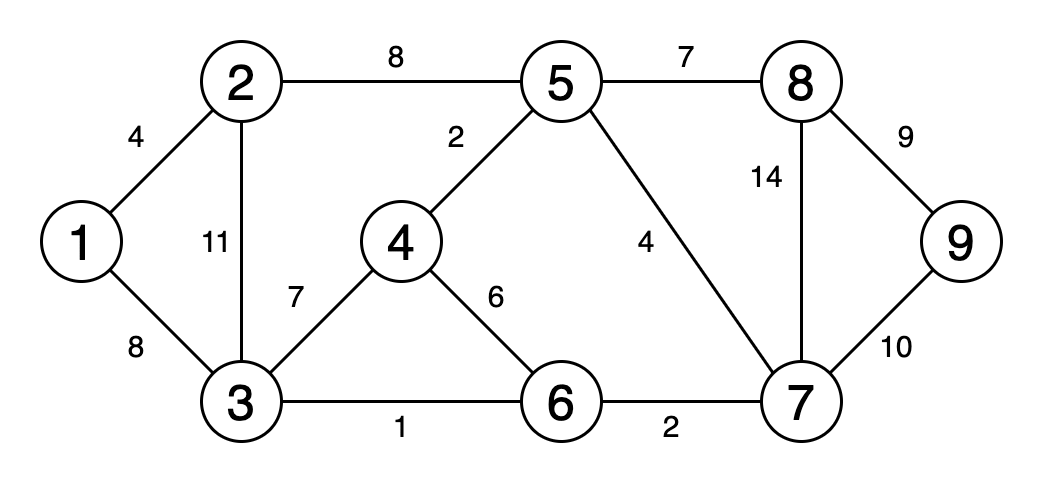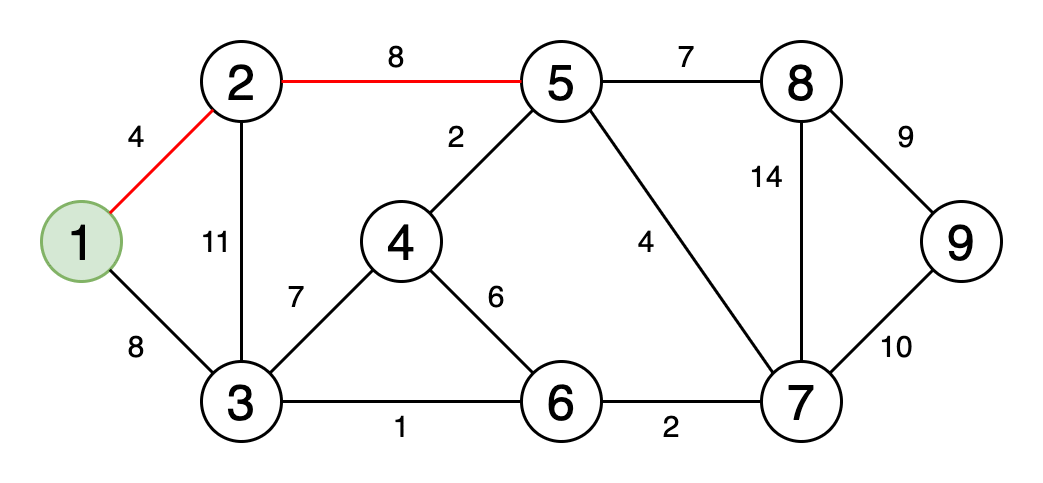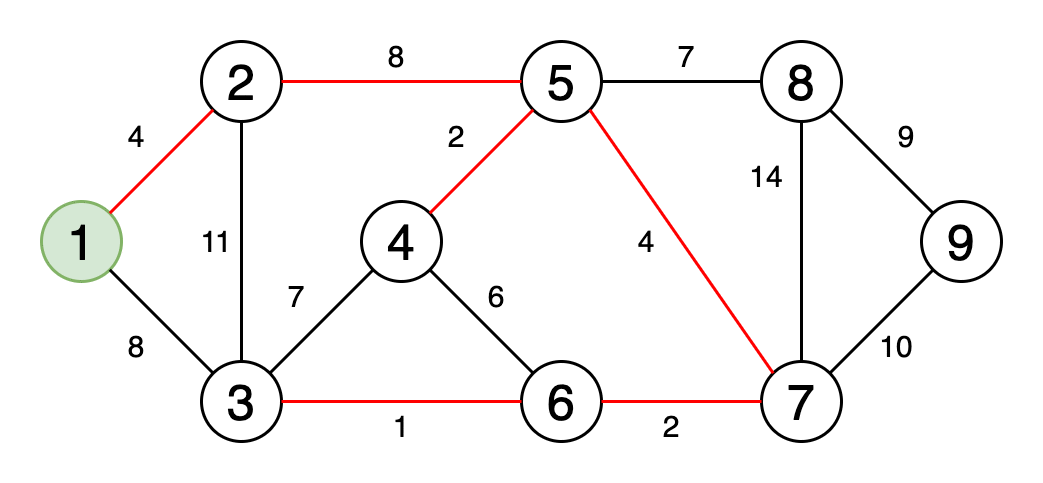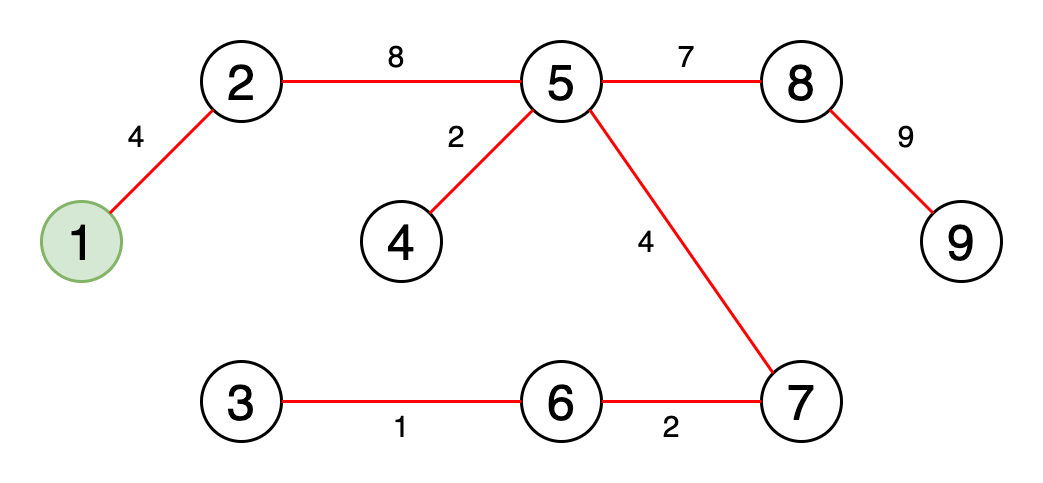
5.最小生成树
最小生成树是图的边缘的子集,该图以最小的边权重之和连接所有顶点,并且不包含循环。
图6是一个动画,显示了获取最小生成树的过程。
演算法
- Prim的算法
- Kruskal的算法
应用领域
- 用于构造树以在计算机网络中广播。
- 用于基于图的聚类分析。
- 用于图像分割。
- 用于将社会区域划分为连续区域的社会地理区域的区域化。
6.牢固连接的组件
如果图中的每个顶点均可从其他每个顶点到达,则称该图是牢固连接的。
图7显示了一个示例图,其中包含三个具有红色,绿色和黄色的顶点的牢固连接的组件。
演算法
- Kosaraju的算法
- Tarjan的强连接组件算法
应用领域
- 用于计算Dulmage–Mendelsohn分解,这是二部图边缘的分类。
- 用于社交网络中,以找到一群紧密联系并根据共同兴趣提出建议的人。
7.拓扑排序
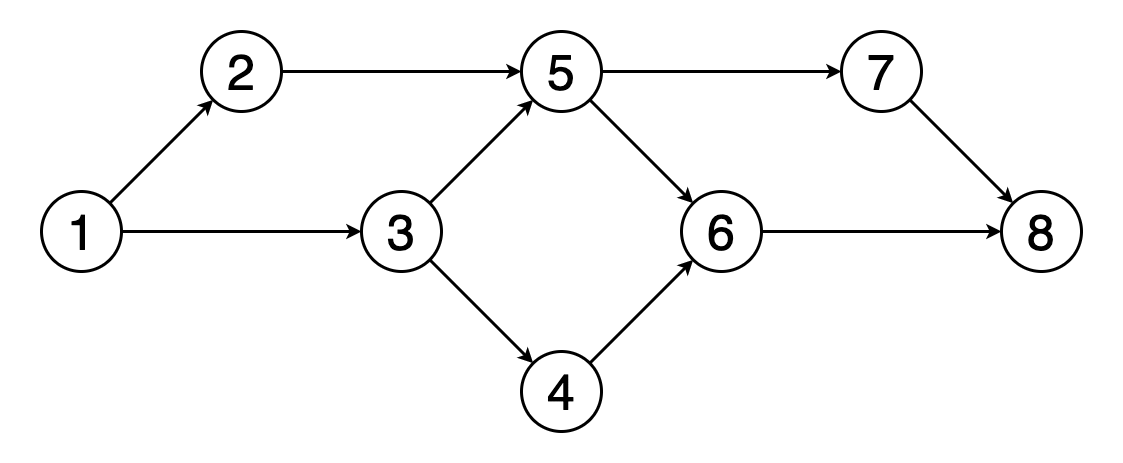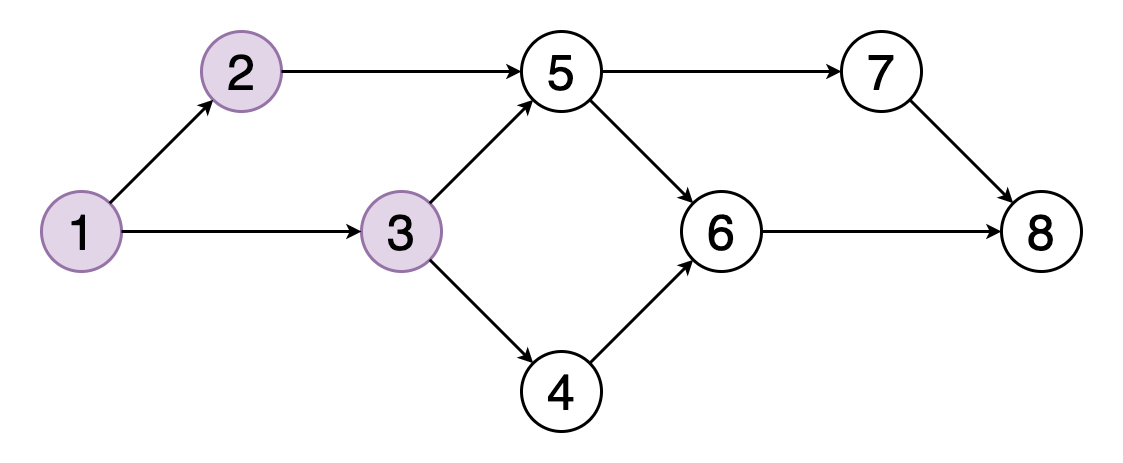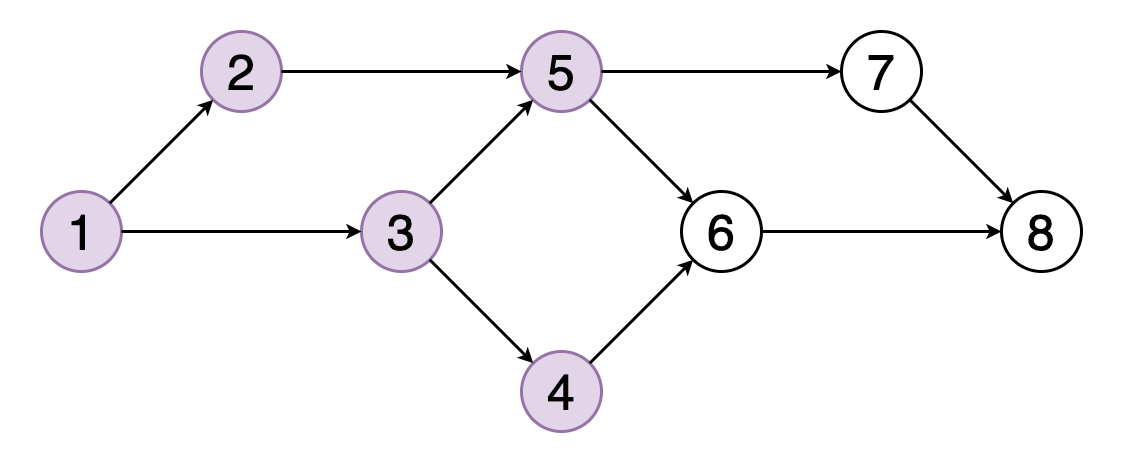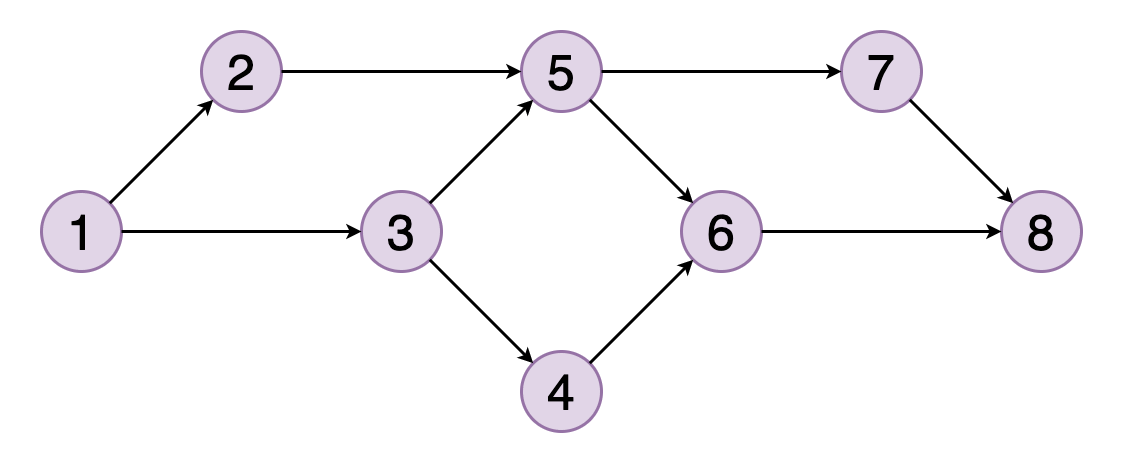
图的拓扑排序是其顶点的线性排序,因此对于排序中的每个有向边(u,v),顶点u都位于v之前。
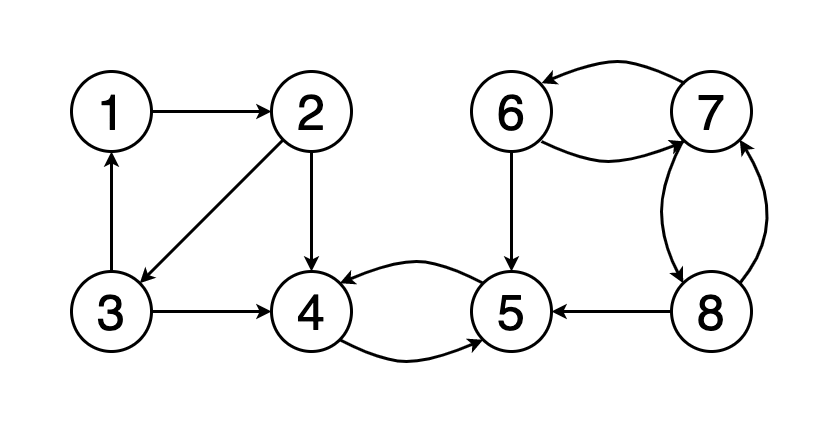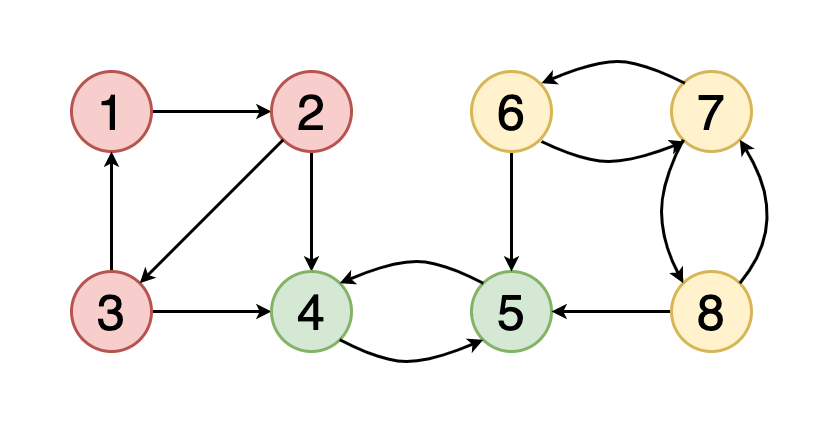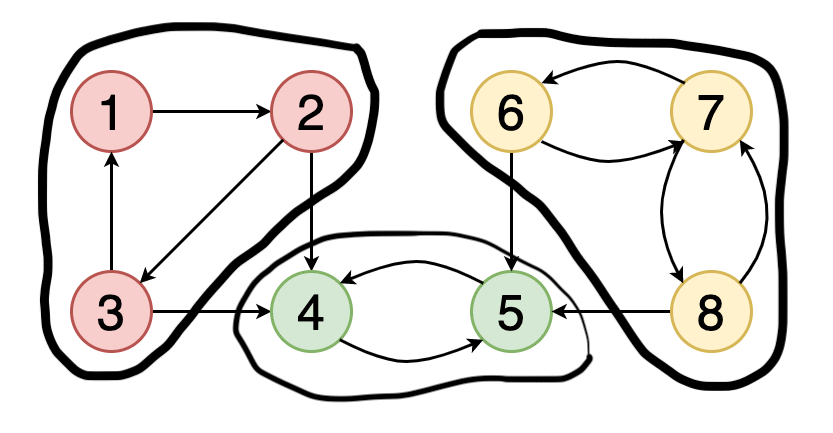
图8显示了顶点(1、2、3、5、4、6、7、8)的拓扑顺序的示例。 您可以看到顶点5应该位于顶点2和3之后。类似地,顶点6应该位于顶点4和5之后。
演算法
- 卡恩算法
- 基于深度优先搜索的算法
应用领域
- 用于指令调度。
- 用于数据序列化。
- 用于确定在makefile中执行的编译任务的顺序。
- 用于解析链接器中的符号依赖性。
8.图形着色
图形着色可在确保某些条件的同时为图形元素分配颜色。 顶点着色是最常用的图形着色技术。 在顶点着色中,我们尝试使用k种颜色为图形的顶点着色,并且任何两个相邻的顶点都不应具有相同的颜色。 其他着色技术包括边缘着色和面部着色。
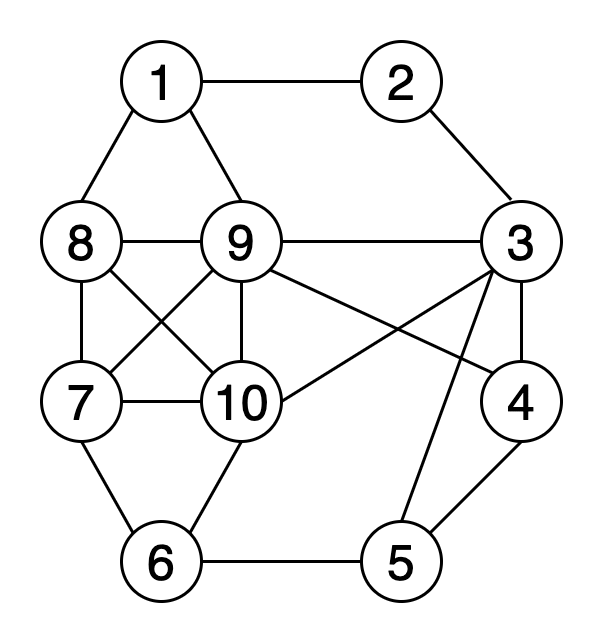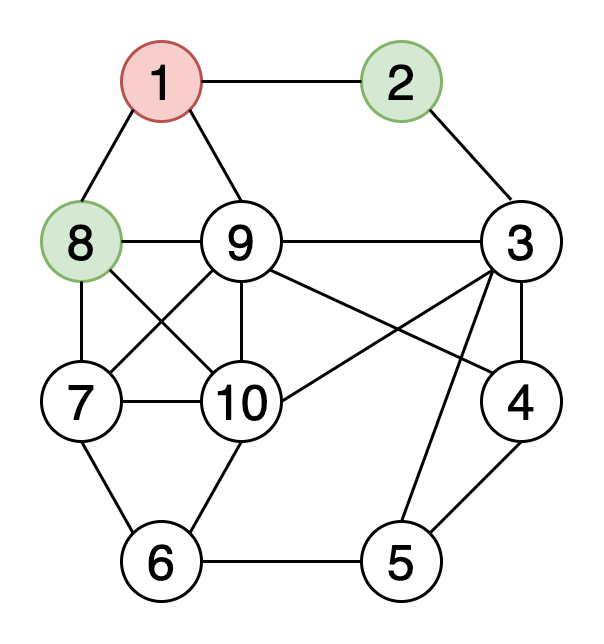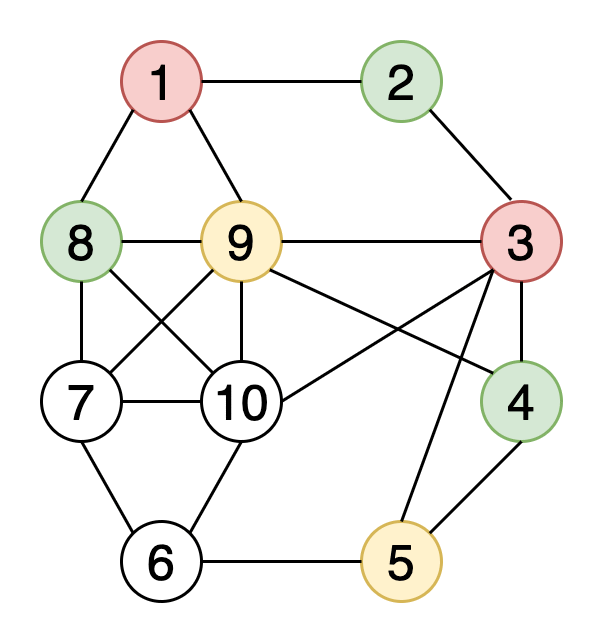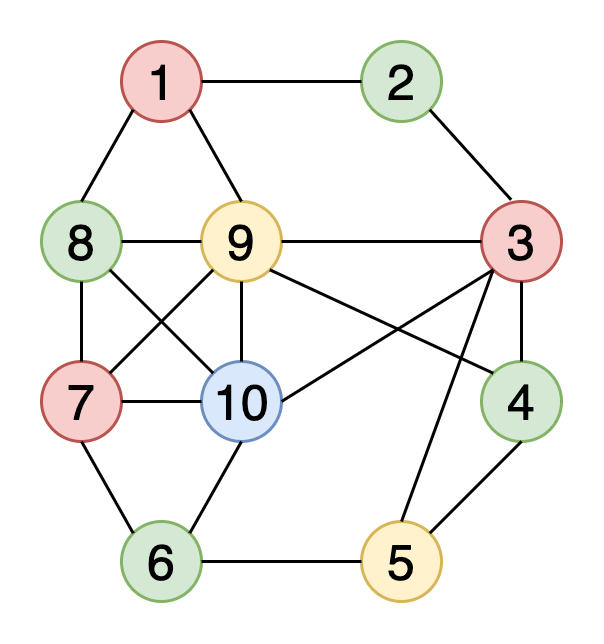
图的色数是为图着色所需的最少颜色数。
图9显示了使用4种颜色的示例图的顶点着色。
演算法
- 使用广度优先搜索或深度优先搜索的算法
- 贪婪的着色
应用领域
- 用于安排时间表。
- 用于分配移动无线电频率。
- 用于建模和求解数独游戏。
- 用于检查图是否为二部图。
- 用于为相邻国家或地区具有不同颜色的国家或州的地理地图着色。
9.最大流量
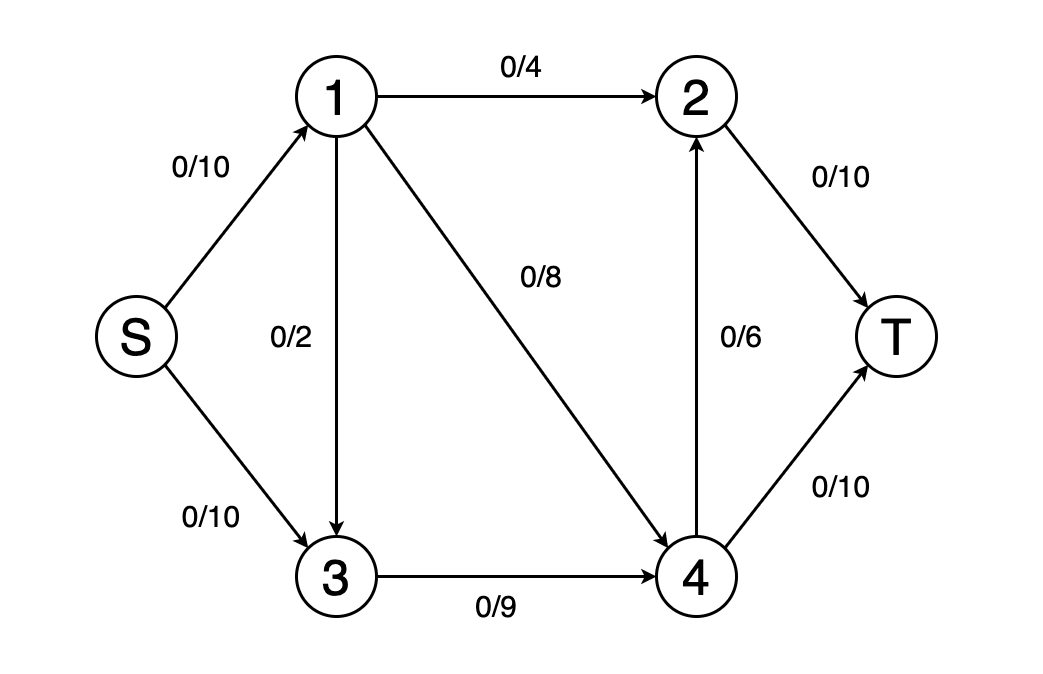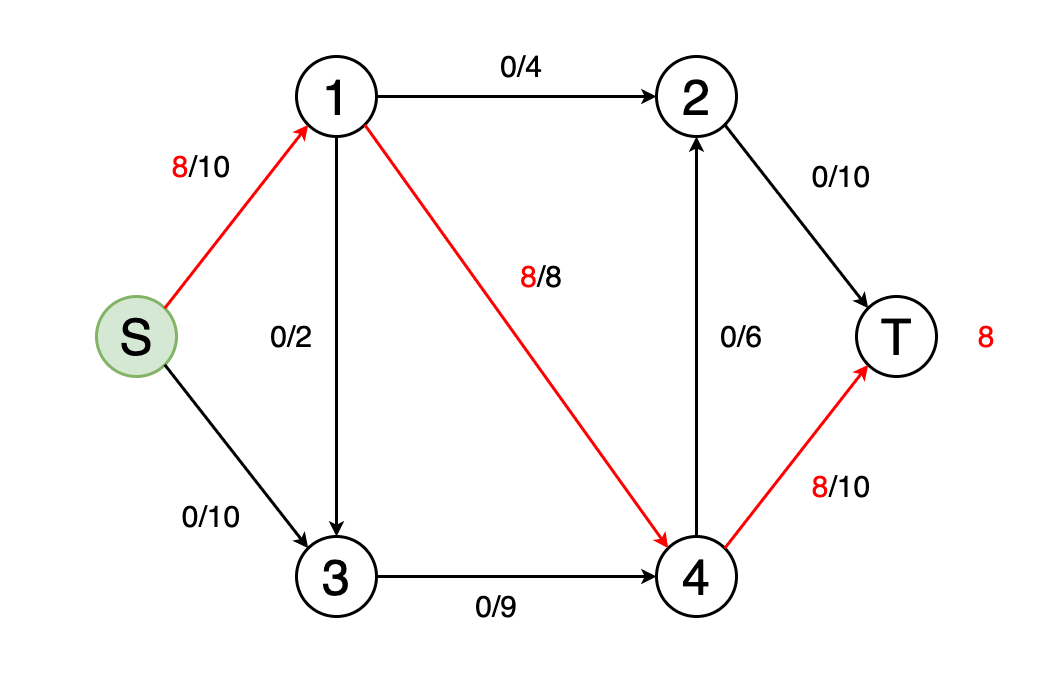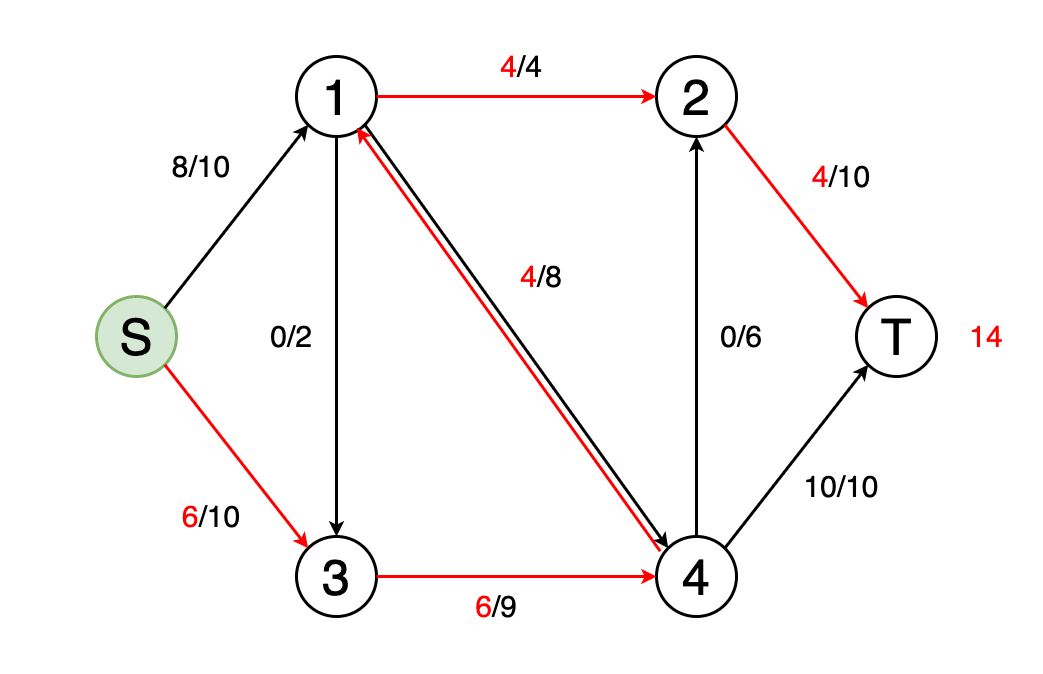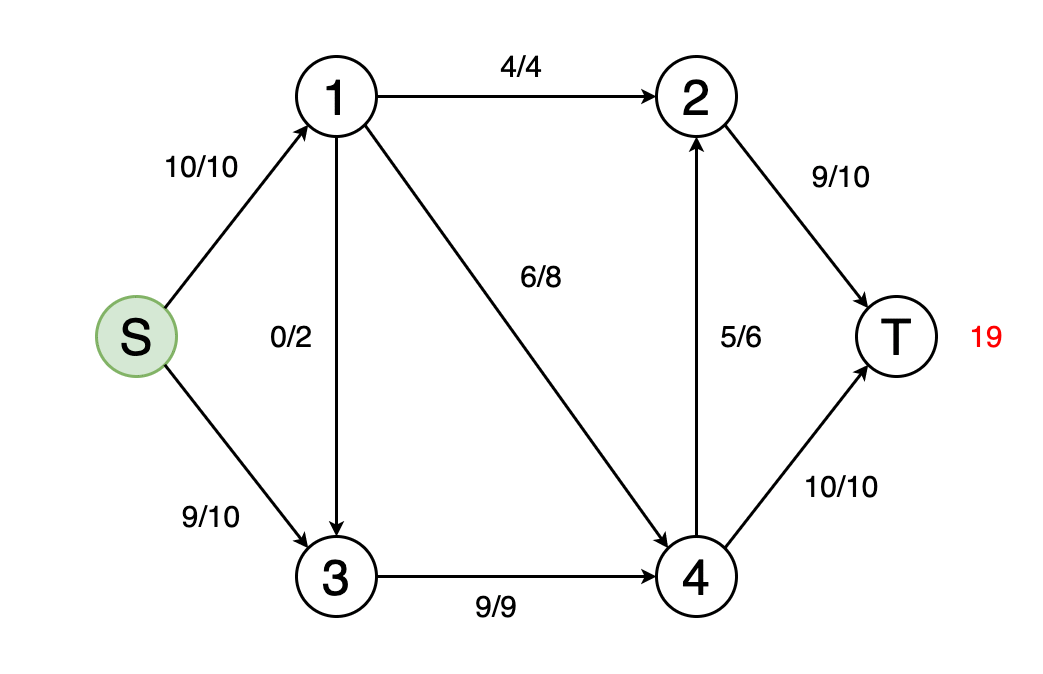
我们可以将图建模为以边权重为流量的流量网络。 在最大流量问题中,我们必须找到一条可以获得最大可能流量的流路。
图10显示了确定网络的最大流量并确定最终流量值的动画示例。
演算法
- 福特-福克森算法
- Edmonds–Karp算法
- Dinic的算法
应用领域
- 用于航空公司调度以调度飞行人员。
- 用于图像分割以查找图像中的背景和前景。
- 用于淘汰无法赢得足够比赛来赶上其所在部门的领先者的棒球队。
10.匹配
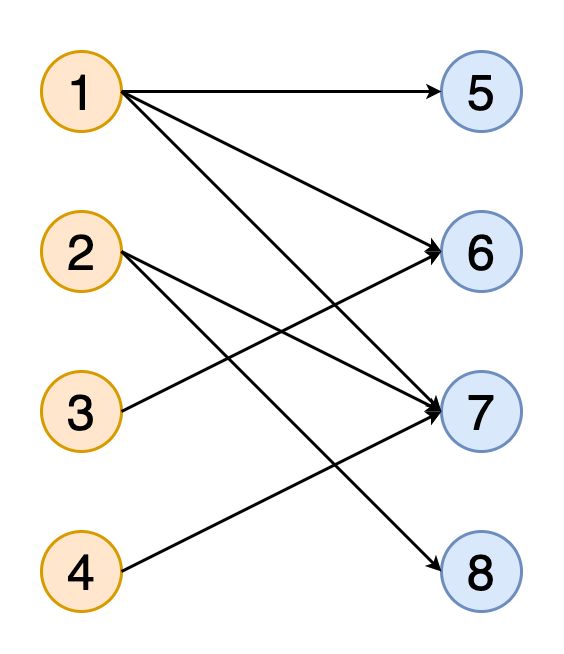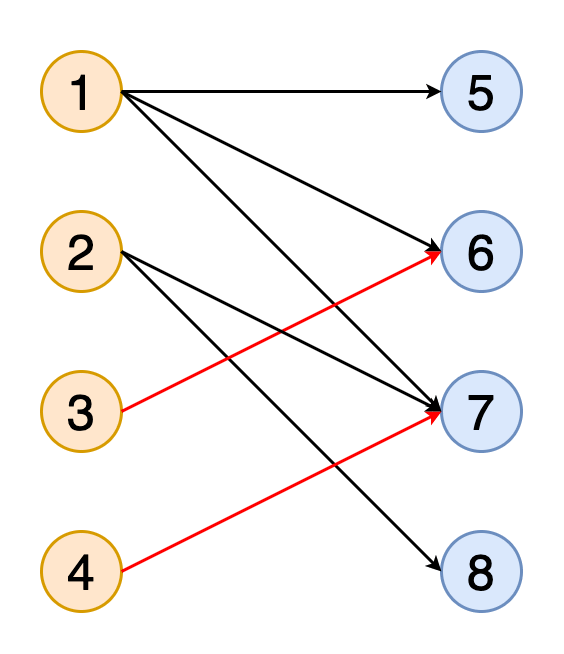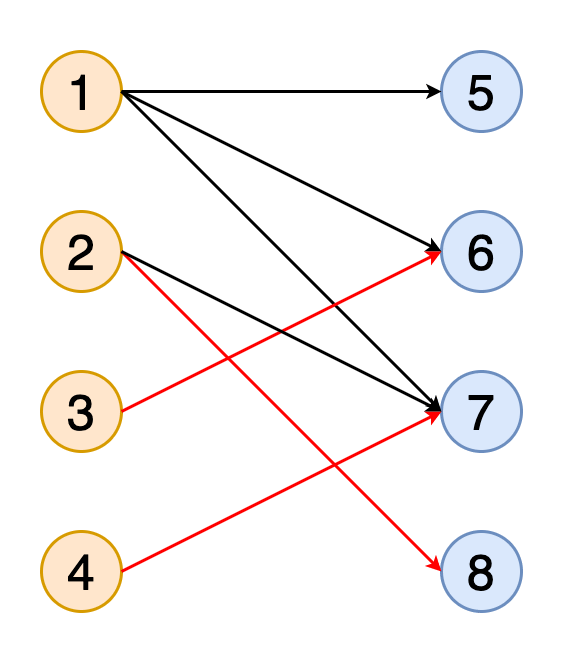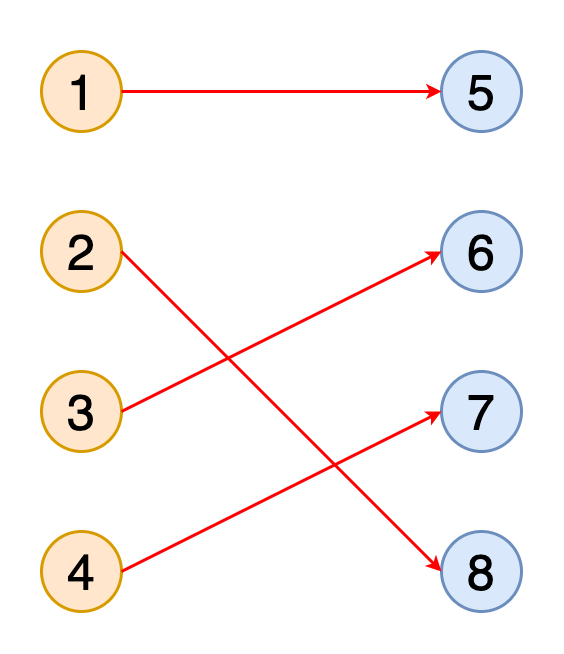
图中的匹配项是一组没有共同顶点的边(即,没有两个边共享共同的顶点)。 如果匹配包含尽可能多的与尽可能多的顶点匹配的边,则该匹配称为最大匹配。
图11显示了获得二部图与橙色和蓝色表示的两组顶点的完全匹配的动画。
演算法
- Hopcroft-Karp算法
- 匈牙利算法
- 开花算法
应用领域
- 用于对接会以匹配新娘和新郎(稳定的婚姻问题)。
- 用于确定顶点覆盖率。
- 在运输理论中用于解决资源分配和出行优化中的问题。
最后的想法
我希望您觉得这篇文章对图形算法进行简单而概括的介绍很有用。 我很想听听您的想法。
非常感谢您的阅读。