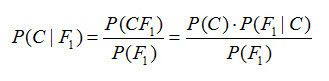有一个函数f(x),它的计算成本很高,甚至不一定是解析表达式,而且导数未知。你的任务是,找出全局最小值。当然,这个任务挺难的,比机器学习中的其他优化问题要难得多。例如,梯度下降可以获得函数的导数,并利用数学捷径来更快地计算表达式。
另外,在某些优化场景中,函数的计算成本很低。如果可以在几秒钟内得到数百个输入值x的变量结果,简单的网格搜索效果会更好。另外,还可以使用大量非传统的非梯度优化方法,如粒子群算法或模拟退火算法(simulated annealing)。
但是,当前的任务没有还没这么高级。优化层面有限,主要包括:
- 计算成本高。理想情况下,我们能够对函数进行足够的查询,从而从本质上复制它,但是采用的优化方法必须在有限的输入采样中才能起作用。
- 导数未知。梯度下降及其风格仍然是最流行的深度学习方法,甚至有时在其他机器学习算法中也备受欢迎的原因所在。导数给了优化器方向感,不过我们没有导数。
- 需要找出全局最小值,即使对于梯度下降这样精细的方法,这也是一项困难的任务。模型需要某种机制来避免陷入局部最小值。
我们的解决方案是贝叶斯优化,它提供了一个简洁的框架来处理类似于场景描述的问题,以最精简的步骤数找到全局最小值。
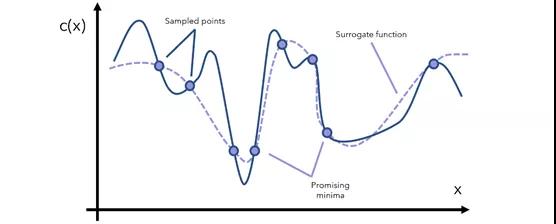
构造一个函数c(x)的假设例子,或者给定输入值x的模型的成本。当然,这个函数看起来是什么样子对优化器是隐藏的——这就是c(x)的真实形状,行话中被称为“目标函数”。
贝叶斯优化通过代理优化方法来完成这项任务。代理函数(surrogate function)是指目标函数的近似函数,是基于采样点形成的。
代理函数可以帮助确定哪些点是可能的最小值。我们决定从这些有希望的区域中抽取更多样本,并相应地更新代理函数。
在每次迭代中继续查看当前的代理函数,通过抽样了解相关感兴趣领域的更多信息并更新函数。注意,代理函数的计算成本要低得多。例如,y=x即是近似函数,计算成本更高,即在一定范围内的y=arcsin((1-cos converx)/sin x))。
经过一定次数的迭代,最终一定会得到一个全局最小值,除非函数的形状非常奇怪(因为它有大幅度且不稳定的波动),这时出现了一个比优化更有意义的问题:你的数据出了什么问题?
让我们来欣赏一下贝叶斯优化之美。它不做任何关于函数的假设(除了首先假设它本身是可优化的),不需要关于导数的信息,并且能够巧妙地使用一个不断更新的近似函数来使用常识推理,对原始目标函数的高成本评估根本不是问题。这是一种基于替代的优化方法。
所以,贝叶斯理论到底是什么呢?贝叶斯统计和建模的本质是根据新信息更新之前的函数(先验函数),产生一个更新后的函数(后验函数)。这正是代理优化在本例中的作用,可以通过贝叶斯理论、公式和含义来进行最佳表达。
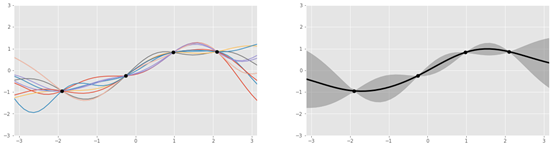
仔细看看代理函数,它通常由高斯过程表示,可以被视为一个骰子,返回适合给定数据点(例如sin、log)的函数,而不是数字1到6。这个过程返回几个函数,这些函数都带有概率。
左:四个数据点的几个高斯过程生成的函数。右:函数聚合。| 图源:Oscar Knagg
使用GP而不是其他曲线拟合方法来建模代理函数,是因为它本质上是贝叶斯的。GP是一个概率分布,类似一个事件的最终结果的分布(例如,1/2的概率抛硬币),但是覆盖了所有可能的函数。
例如,将当前数据点集定义为40%可由函数a(x)表示,10%可由函数b(x)表示。通过将代理函数表示为概率分布,可以通过固有的概率贝叶斯过程更新信息。当引入新信息时,可能只有20%的数据可用函数a(x)表示。这些变化是由贝叶斯公式控制的。如果使用多项式回归来拟合新的数据点,难度就加大了,甚至不可能实现。
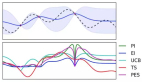
代理函数表示为概率分布,先验函数被更新为“采集函数”。该函数负责权衡探索和利用问题驱动新点的命题进行测试:
· “利用函数”试图进行取样以便代理函数预测最合适的最小值,这是利用已知的可能的点。然而,如果我们已经对某一区域进行了足够的探索,那么继续利用已知的信息将不会有什么收获。
· “探索函数”试图在不确定性高的地方取样。这就确保了空间中没有什么主要区域是未知的——全局最小值可能恰好就在那里。
一个鼓励多利用和少探索的采集函数将导致模型只停留在它首先找到的最小值(通常是局部的——“只去有光的地方”)。反之,模型则首先不会停留在局部或全局的最小值上,而是在微妙的平衡中寻求最佳结果。
用a(x)表示采集函数,必须同时考虑探索和利用。常见的采集函数包括预期改进和最大改进概率,所有这些函数都度量了给定的先验信息(高斯过程)下,特定输入值在未来获得成功的概率。
结合以上所有内容,贝叶斯优化的原理如下:
- 初始化一个高斯过程的“代理函数”先验分布。
- 选择多个数据点x,使运行在当前先验分布上的采集函数a(x)最大化。
- 对目标成本函数c(x)中的数据点x进行评估,得到结果y。
- 用新的数据更新高斯过程的先验分布,产生后验(在下一步将成为先验)。
- 重复步骤2-5进行多次迭代。
- 解释当前的高斯过程分布(成本极低)来找到全局最小值。
贝叶斯优化就是把概率的概念建立在代理优化的基础之上。这两种概念的结合创造了一个功能强大的系统,应用范围广阔,从制药产品开发到自动驾驶汽车都有相关应用。
然而,在机器学习中最常见的是用于超参数优化。例如,如果要训练一个梯度增强分类器,从学习率到最大深度到最小杂质分割值,有几十个参数。在本例中,x表示模型的超参数,c(x)表示模型的性能,给定超参数x。
使用贝叶斯优化的主要目的在于应对评估输出非常昂贵的情况。首先,需要用这些参数建立一个完整的树集合,其次,它们需要经过多次预测,这对于集合而言成本极高。
可以说,神经网络评估给定参数集的损失更快:简单地重复矩阵乘法,这是非常快的,特别是在专用硬件上。这就是使用梯度下降法的原因之一,它需要反复查询来了解其发展方向。
图源:unsplash
总结一下,我们的结论是:
· 代理优化使用代理函数或近似函数来通过抽样估计目标函数。
· 贝叶斯优化通过将代理函数表示为概率分布,将代理优化置于概率框架中,并根据新信息进行更新。
· 采集函数用于评估探索空间中的某个点将产生“良好”结果的概率,给定目前从先验已知的信息,平衡探索和利用的问题。
· 主要在评估目标函数成本昂贵时使用贝叶斯优化,通常用于超参数调优。有许多像HyperOpt这样的库可以实现这个功能。
贝叶斯优化之美,你感受到了吗?
本文转载自微信公众号「读芯术」,作者读芯术。转载本文请联系读芯术公众号。