本文转载自微信公众号「Java中文社群」,作者磊哥 。转载本文请联系Java中文社群公众号。
这正式开始之前,先给大家再解释一下「堆栈」一词的含义,因为之前有读者对这个词有一定的疑惑。
Stack 翻译为中文是堆栈的意思,但为了能和 Heap(堆)区分开,因此我们一般将 Stack 简称为栈。因此当“堆栈”连在一起时有可能表示的是 Stack,而当“堆、栈”中间有分号时,则表示 Heap(堆)和 Stack(栈),如下图所示:
JDK 栈的实现
聊会正题,接下来我们来看 JDK 中是如何实现栈的?
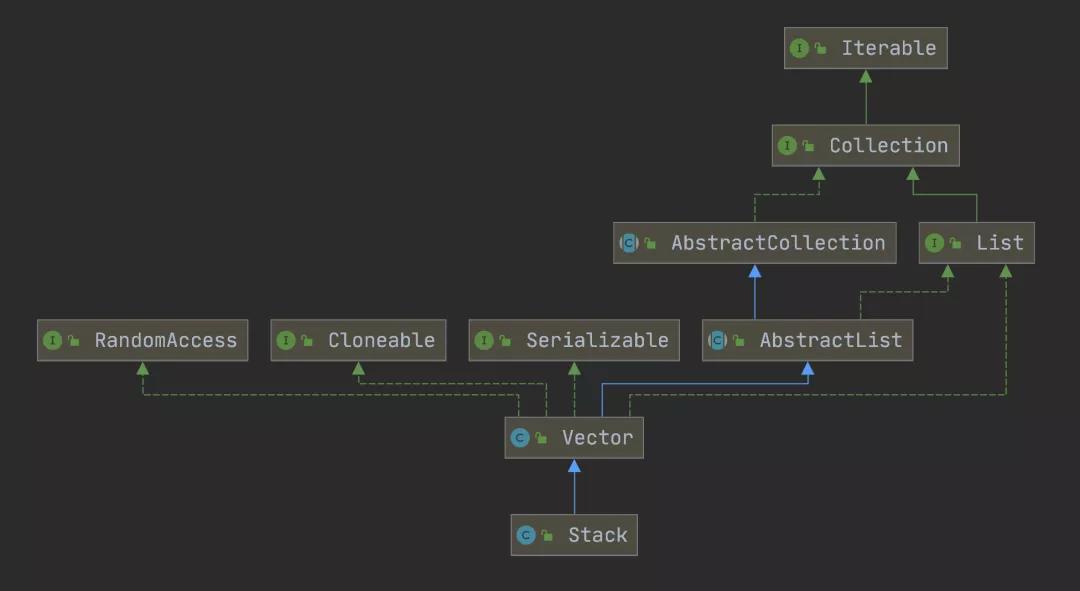
在 JDK 中,栈的实现类是 Stack,它的继承关系如下图所示:
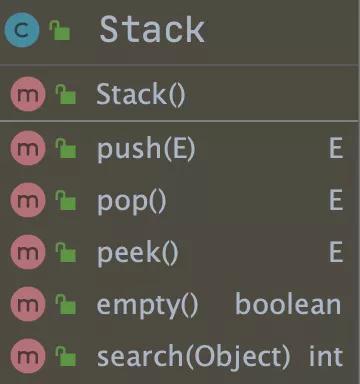
Stack 包含的方法如下图所示:
其中最重要的方法有:
- push:入栈方法(添加数据);
- pop:出栈并返回当前元素(移除数据);
- peek:查询栈顶元素。
Stack 实现源码如下:
- public class Stack<E> extends Vector<E> {
- /**
- * 创建一个空栈
- */
- public Stack() {
- }
- /**
- * 入栈方法,调用的是 Vector#addElement 的添加方法
- */
- public E push(E item) {
- addElement(item);
- return item;
- }
- /**
- * 出栈并返回当前元素,调用的是 Vector#removeElementAt 的移除元素方法
- */
- public synchronized E pop() {
- E obj; // 返回当前要移除的栈顶元素信息
- int len = size();
- obj = peek(); // 查询当前栈顶元素
- removeElementAt(len - 1); // 移除栈顶元素
- return obj;
- }
- /**
- * 查询栈顶元素,调用 Vector#elementAt 的查询方法
- */
- public synchronized E peek() {
- int len = size(); // 查询当前栈的长度
- if (len == 0) // 如果为空栈,直接抛出异常
- throw new EmptyStackException();
- return elementAt(len - 1); // 查询栈顶元素的信息
- }
- /**
- * 判断栈是否为空
- */
- public boolean empty() {
- return size() == 0;
- }
- // 忽略其他方法...
- }
从上述源码可以看出, Stack 中的核心方法中都调用了父类 Vector 类中的方法,Vector 类的核心源码:
- public class Vector<E>
- extends AbstractList<E>
- implements List<E>, RandomAccess, Cloneable, java.io.Serializable
- {
- protected Object[] elementData; // 存储数据的容器
- protected int elementCount; // 存储数据的容量值
- /**
- * 添加数据
- */
- public synchronized void addElement(E obj) {
- modCount++; // 统计容器被更改的参数
- ensureCapacityHelper(elementCount + 1); // 确认容器大小,如果容量超出则进行扩容
- elementData[elementCount++] = obj; // 将数据存储到数组
- }
- /**
- * 移除元素(根据下标移除)
- */
- public synchronized void removeElementAt(int index) {
- modCount++; // 统计容器被更改的参数
- // 数据正确性效验
- if (index >= elementCount) {
- throw new ArrayIndexOutOfBoundsException(index + " >= " +
- elementCount);
- }
- else if (index < 0) {
- throw new ArrayIndexOutOfBoundsException(index);
- }
- int j = elementCount - index - 1;
- if (j > 0) { // 删除的不是最后一个元素
- // 把删除元素之后的所有元素往前移动
- System.arraycopy(elementData, index + 1, elementData, index, j);
- }
- elementCount--; // 数组容量 -1
- elementData[elementCount] = null; // 将末尾的元素赋值为 null(删除尾部元素)
- }
- /**
- * 查询元素(根据下标)
- */
- public synchronized E elementAt(int index) {
- // 安全性验证
- if (index >= elementCount) {
- throw new ArrayIndexOutOfBoundsException(index + " >= " + elementCount);
- }
- // 根据下标返回数组中的元素
- return elementData(index);
- }
- // 忽略其他方法...
- }
对于上述源码中,可以最不好理解的就是 System#arraycopy 这个方法,它的作用其实就是将删除的元素(非末尾元素)的后续元素依次往前移动的,比如以下代码:
- Object[] elementData = {"Java", "Hello", "world", "JDK", "JRE"};
- int index = 3;
- int j = elementData.length - index - 1;
- System.arraycopy(elementData, index + 1, elementData, index, j);
- // System.arraycopy(elementData, 4, elementData, 3, 1);
- System.out.println(Arrays.toString(elementData));
它的运行结果是:
- [Java, Hello, world, JRE, JRE]
也就是说当我们要删除下标为 3 的元素时,需要把 3 以后的元素往前移动,所以数组的值就从 {"Java", "Hello", "world", "JDK", "JRE"} 变为了 [Java, Hello, world, JRE, JRE],最后我们只需要把尾部元素删除掉,就可以实现数组中删除非末尾元素的功能了。
小结
通过以上源码可以得知,JDK 中的栈(Stack)也是通过物理结构数组实现的,我们通过操作物理数组来实现逻辑结构栈的功能。
栈的应用
经过前面的学习我们对栈已经有了一定的了解了,那栈在我们的平常工作中有哪些应用呢?接下里我们一起来看。
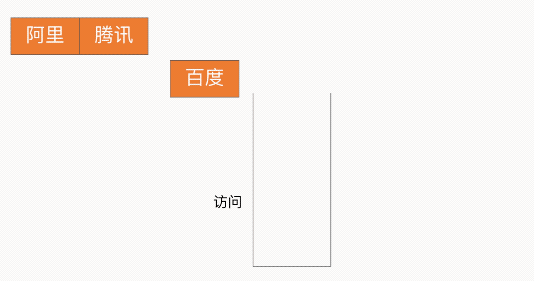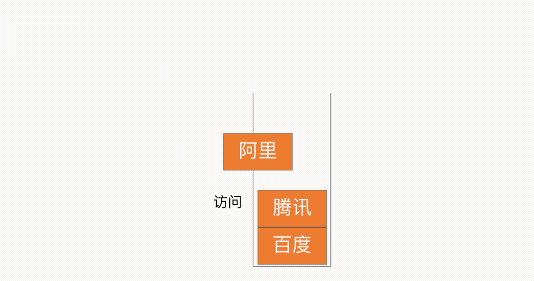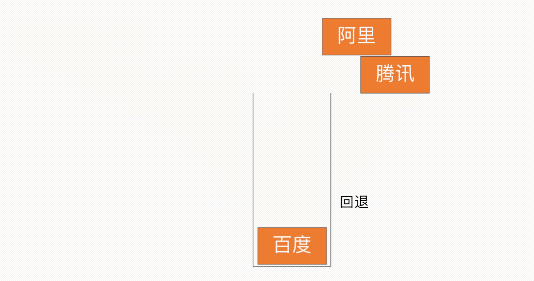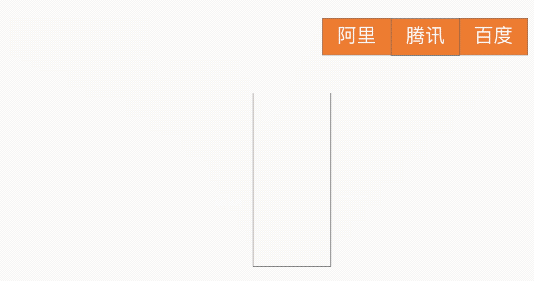
浏览器回退
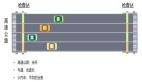
栈的特性为 LIFO(Last In First Out,LIFO)后进先出,因此借助此特性就可以实现浏览器的回退功能,如下图所示:
函数调用栈
栈在程序中最经典的一个应用就是函数调用栈了(或叫方法调用栈),比如操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数,就会将临时变量作为一个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈。为了让你更好地理解,我们一块来看下这段代码的执行过程。
- int main() {
- int a = 1;
- int ret = 0;
- int res = 0;
- ret = add(3, 5);
- res = a + ret;
- System.out.println(res);
- reuturn 0;
- }
- int add(int x, int y) {
- int sum = 0;
- sum = x + y;
- return sum;
- }
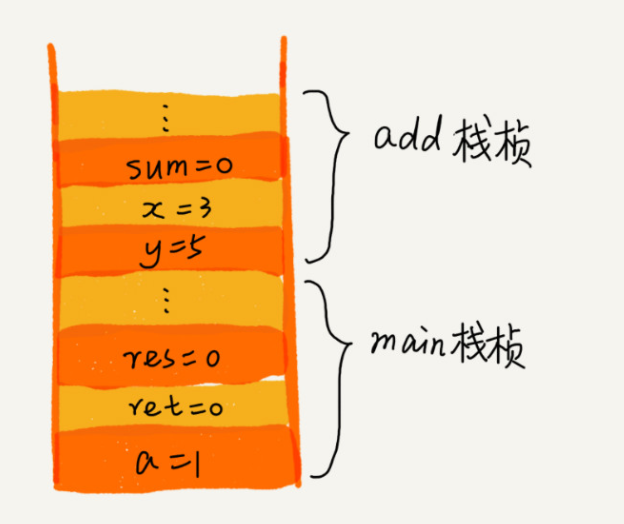
从代码中我们可以看出, main() 函数调用了 add() 函数,获取计算结果,并且与临时变量 a 相加,最后打印 res 的值。为了让你清晰地看到这个过程对应的函数栈里出栈、入栈的操作,我画了一张图。图中显示的是,在执行到 add() 函数时,函数调用栈的情况。
栈的复杂度
复杂度分为两个维度:
- 时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述;
- 空间维度:是指执行当前算法需要占用多少内存空间,我们通常用「空间复杂度」来描述。
这两种复杂度都是用大 O 表示法来表示的,比如以下代码:
- int[] arr = {1, 2, 3, 4};
- for (int i = 0; i < arr.length; i++) {
- System.out.println(i);
- }
用大 O 表示法来表示的话,它的时间复杂度就是 O(n),而如下代码的时间复杂度却为 O(1):
- int[] arr = {1, 2, 3, 4};
- System.out.println(arr[0]); // 通过下标获取元素
因此如果使用大 O 表示法来表示栈的复杂度的话,结果如下所示:
引用 & 鸣谢
https://time.geekbang.org/column/article/41222