结构与算法：二叉树与多叉树-多叉树转化为二叉树

一、树状结构

1、数组与链表

数组结构

数组存储是通过下标方式访问元素，查询速度快，如果数组元素是有序的，还可使用二分查找提高检索速度;如果添加新元素可能会导致多个下标移动，效率较低;

链表结构

链表存储元素，对于元素添加和删除效率高，但是遍历元素每次都需要从头结点开始，效率特别低;

树形结构能同时相对提高数据存储和读取的效率。

2、树结构概念

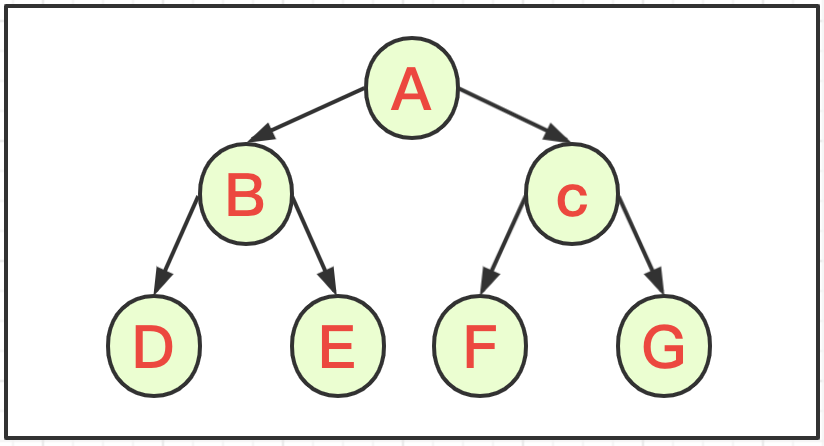
根节点：树的根源，没有父节点的节点，如上图A节点;
兄弟节点：拥有同一父节点的子节点。如图B与C点;
叶子节点：没有子节点的节点。如图DEFG节点;
树的高度：最大层数，如图为3层;
路径：从root根节点找到指定节点的路线;

树形结构是一层次的嵌套结构。一个树形结构的外层和内层有相似的结构，所以这种结构多可以递归的表示。经典数据结构中的各种树状图是一种典型的树形结构：一颗树可以简单的表示为根，左子树，右子树。左子树和右子树又有自己的子树。

二、二叉树模型

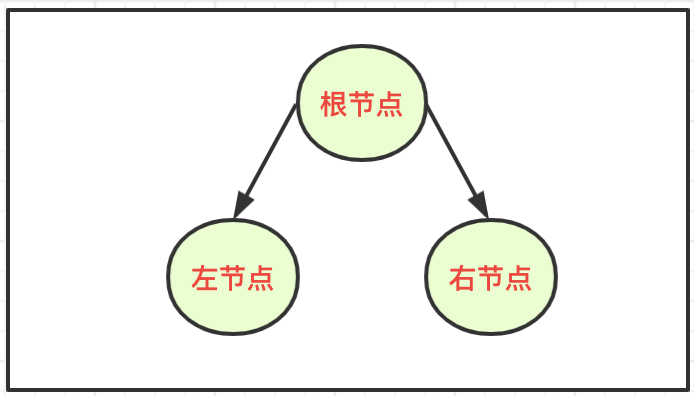
树的种类有很多，二叉树(BinaryTree)是树形结构的一个重要类型，每个节点最多只能有两个子节点的一种形式称为二叉树，二叉树的子节点分为左节点和右节点，许多实际问题抽象出来的数据结构往往是二叉树形式。

完全二叉树

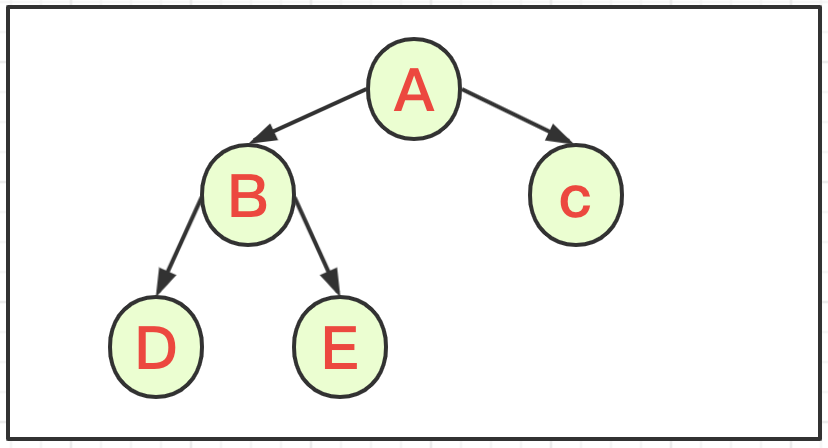
二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，我们称为完全二叉树

满二叉树

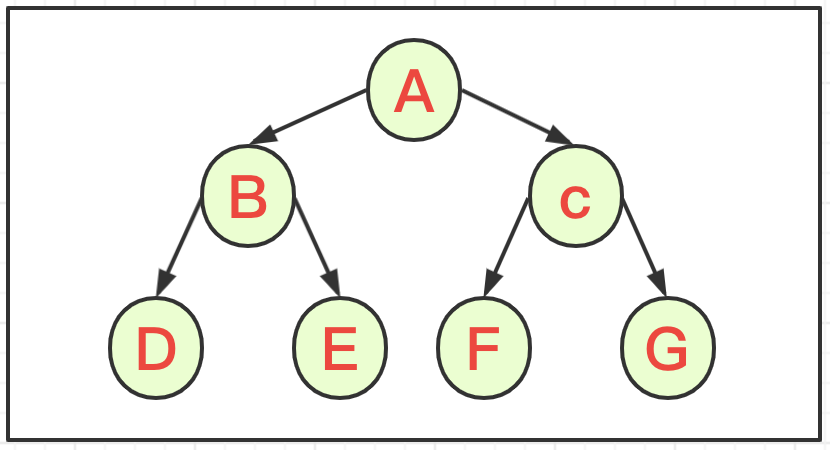
当二叉树的所有叶子节点都在最后一层，并且结点总数= 2^n -1 , n 为层数，则称为满二叉树。

平衡二叉树

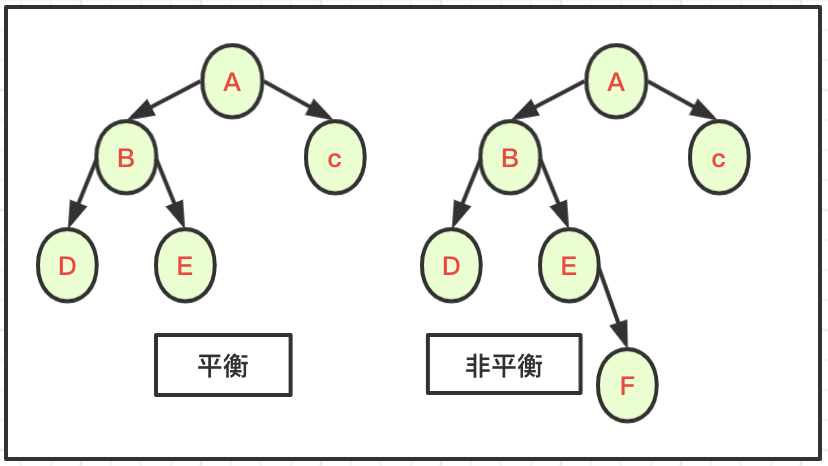
平衡二叉树指的是，任意节点的子树的高度差的绝对值都小于等于1，并且左右两个子树都是一棵平衡二叉树，常见的符合平衡树的有，B树(多路平衡搜索树)、AVL树(二叉平衡搜索树)等。

二叉查找树

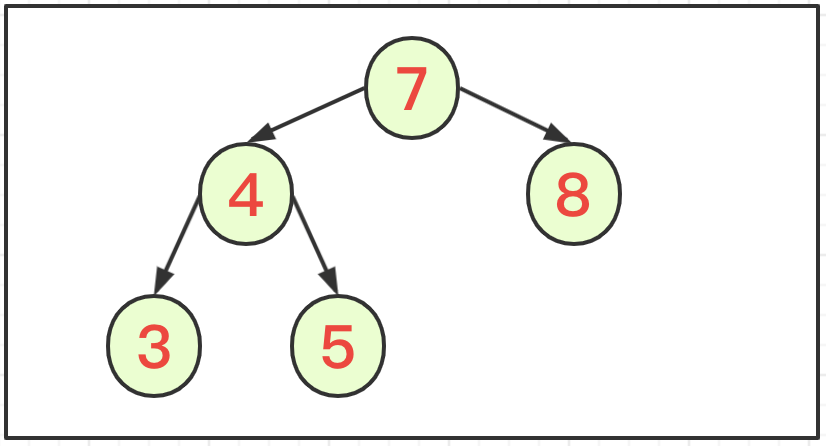
二叉查找树(BinarySearchTree)不但二叉树，同时满足一定的有序性：节点的左子节点比自己小，节点的右子节点比自己大。

三、二叉树编码

1、基础代码

节点代码

class TreeNode { 
    private String num ; 
    private TreeNode leftNode ; 
    private TreeNode rightNode ; 
    public TreeNode(String num) { 
        this.num = num; 
    }    @Override 
    public String toString() { 
        return "TreeNode{num=" + num +'}'; 
    }} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

树结构代码

class BinaryTree01 { 
    private TreeNode root ; 
} 
1.
2.
3.

2、遍历与查找

前序遍历查找

先处理当前结点的数据，再依次递归遍历左子树和右子树;

public void prevTraverse() { 
    // 输出父结点 
    System.out.println(this); 
    // 向左子树递归前序遍历 
    if(this.leftNode != null) { 
        this.leftNode.prevTraverse(); 
    }    // 向右子树递归前序遍历 
    if(this.rightNode != null) { 
        this.rightNode.prevTraverse(); 
    }}public TreeNode prevSearch(String num) {    //比较当前结点 
    if(this.num.equals(num)) { 
        return this ; 
    }    // 递归遍历左子树查找 
    TreeNode findNode = null; 
    if(this.leftNode != null) { 
        findNode = this.leftNode.prevSearch(num); 
    }    // 左子树遍历命中 
    if(findNode != null) { 
        return findNode ; 
    }    // 递归遍历右子树查找 
    if(this.rightNode != null) { 
        findNode = this.rightNode.prevSearch(num); 
    }    return findNode ; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.

中序遍历查找

先递归遍历左子树，再处理父节点，再递归遍历右子树

public void midTraverse() { 
    // 向左子树递归中序遍历 
    if(this.leftNode != null) { 
        this.leftNode.midTraverse(); 
    }    // 输出父结点 
    System.out.println(this); 
    // 向右子树递归中序遍历 
    if(this.rightNode != null) { 
        this.rightNode.midTraverse(); 
    }}public TreeNode midSearch(String num) {    // 递归遍历左子树查找 
    TreeNode findNode = null; 
    if(this.leftNode != null) { 
        findNode = this.leftNode.midSearch(num); 
    }    if(findNode != null) { 
        return findNode ; 
    }    // 比较当前结点 
    if(this.num.equals(num)) { 
        return this ; 
    }    // 递归遍历右子树查找 
    if(this.rightNode != null) { 
        findNode = this.rightNode.midSearch(num); 
    }    return findNode ; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.

后序遍历查找

先递归遍历左子树，再递归遍历右子树，最后处理父节点;

public void lastTraverse() { 
    // 向左子树递归后序遍历 
    if(this.leftNode != null) { 
        this.leftNode.lastTraverse(); 
    }    // 向右子树递归后序遍历 
    if(this.rightNode != null) { 
        this.rightNode.lastTraverse(); 
    }    // 输出父结点 
    System.out.println(this); 
}public TreeNode lastSearch(String num) {    // 递归遍历左子树查找 
    TreeNode findNode = null; 
    if(this.leftNode != null) { 
        findNode = this.leftNode.lastSearch(num); 
    }    if(findNode != null) { 
        return findNode ; 
    }    // 递归遍历右子树查找 
    if(this.rightNode != null) { 
        findNode = this.rightNode.lastSearch(num); 
    }    if(findNode != null) { 
        return findNode ; 
    }    // 比较当前结点 
    if(this.num.equals(num)) { 
        return this ; 
    }    return null ; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.

3、删除节点

如果当前删除的节点是叶子节点，则可以直接删除该节点;如果删除的节点是非叶子节点，则删除该节点树。

public void deleteNode(String num) { 
    // 判断左节点是否删除 
    if(this.leftNode != null && this.leftNode.num.equals(num)) { 
        this.leftNode = null ; 
        return ; 
    }    // 判断右节点是否删除 
    if(this.rightNode != null && this.rightNode.num.equals(num)) { 
        this.rightNode = null; 
        return ; 
    }    // 向左子树遍历进行递归删除 
    if(this.leftNode != null) { 
        this.leftNode.deleteNode(num); 
    }    // 向右子树遍历进行递归删除 
    if(this.rightNode != null) { 
        this.rightNode.deleteNode(num); 
    }} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

四、多叉树

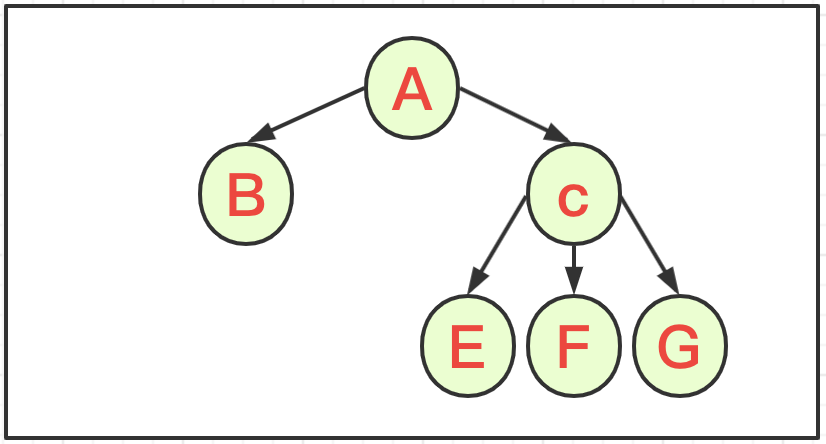
多叉树是指一个父节点可以有多个子节点，但是一个子节点依旧遵循一个父节点定律，通常情况下，二叉树的实际应用高度太高，可以通过多叉树来简化对数据关系的描述。

例如：Linux文件系统，组织架构关系，角色菜单权限管理系统等，通常都基于多叉树来描述。