正则表达式具有伟大技术发明的一切特点,它简单、优美、功能强大、妙用无穷。对于很多实际工作来讲,正则表达式简直是灵丹妙药,能够成百倍地提高开发效率和程序质量。
1. 正则常见规则
1.1 字符匹配
字符说明\转义符\d[0-9]。表示是一位数字。\D[^0-9]。表示除数字外的任意字符。\w[0-9a-zA-Z_]。表示数字、大小写字母和下划线。\W[^0-9a-zA-Z_]。非单词字符。\s[\t\v\n\r\f]。表示空白符,包括空格、水平制表符、
垂直制表符、换行符、回车符、换页符。\S[^\t\v\n\r\f]。非空白符。.[^\n\r]。通配符,表示几乎任意字符。
换行符、回车符、行分隔符和段分隔符除外。\uxxxx查找以十六进制数 xxxx 规定的 Unicode 字符。\f匹配一个换页符 (U+000C)。\n匹配一个换行符 (U+000A)。\r匹配一个回车符 (U+000D)。\t匹配一个水平制表符 (U+0009)。\v匹配一个垂直制表符 (U+000B)。\0匹配 NULL(U+0000)字符, 不要在这后面跟其它小数,因为 \0是一个
八进制转义序列。[\b]匹配一个退格(U+0008)。(不要和\b 混淆了。)[abc]any of a, b, or c[^abc]not a, b, or c[a-g]character between a & g
1.2 位置匹配
字符说明\b是单词边界,具体就是\w 和\W 之间的位置,也包括\w 和 ^ 之间的位置,
也包括\w 和之间的位置。具体说来就是与、与、与,与之间的位置。\B是\b 的反面的意思,非单词边界。例如在字符串中所有位置中,扣掉\b,
剩下的都是\B 的。^abc$字符串开始、结束的位置
1.3 组
字符说明(abc)capture group,捕获组\nbackreference to group #n,分组引用,引用第 n 个捕获组匹配的内容,
其中 n 是正整数(?:abc)non-capturing group,非捕获组
1.4 先行断言
字符说明a(?=b)positive lookahead,先行断言,a 只有在 b 前面才匹配a(?!b)negative lookahead,先行否定断言,a 只有不在 b 前面才匹配
1.5 后行断言
字符说明(?<=b)apositive lookbehind,后行断言,a 只有在 b 后面才匹配(?<!b)anegative lookbehind,后行否定断言,a 只有不在 b 后面才匹配
1.6 量词和分支
字符说明a*0 or morea+1 or morea?0 or 1a{5}exactly fivea{2,}two or morea{1,3}between one & threea+?
a{2,}?match as few as possible,惰性匹配,就是尽可能少的匹配
以下都是惰性匹配:
{m,n}?
{m,}?
??
+?
*?
1.7 分支
字符说明ab|cdmatch ab or cd,匹配'ab'或者'cd'字符子串
1.8 修饰符
字符说明i执行对大小写不敏感的匹配。g执行全局匹配(查找所有匹配而非在找到第一个匹配后停止)。m执行多行匹配。u开启"Unicode 模式",用来正确处理大于\uFFFF 的 Unicode 字符。也就是说,会正确处理四个字节的 UTF-16 编码。s允许 . 匹配换行符。yy 修饰符的作用与 g 修饰符类似,也是全局匹配,后一次匹配都从上一次匹配成功的下一个位置开始。不同之处在于,g 修饰符只要剩余位置中存在匹配就可,而 y 修饰符确保匹配必须从剩余的第一个位置开始,这也就是"粘连"的涵义
2. 运算符优先级
运算符描述\转义符(), (?:), (?=), []圆括号和方括号*, +, ?, {n}, {n,}, {n,m}限定符^, $, \任何元字符、任何字符定位点和序列(即:位置和顺序)|替换,"或"操作
字符具有高于替换运算符的优先级,使得"m|food"匹配"m"或"food"。若要匹配"mood"或"food",请使用括号创建子表达式,从而产生"(m|f)ood"。
3. 正则回溯
3.1 什么是回溯算法
以下是来自摘自维基百科的部分解释:
回溯法是一种通用的计算机算法,用于查找某些计算问题的所有(或某些)解决方案,特别是约束满足问题,逐步构建候选解决方案,并在确定候选不可能时立即放弃候选("回溯")完成有效的解决方案。
回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
找到一个可能存在的正确的答案
在尝试了所有可能的分步方法后宣告该问题没有答案
在最坏的情况下,回溯法会导致一次复杂度为指数时间的计算。
3.2 什么是正则回溯
正则引擎主要可以分为两大类:一种是 DFA(Deterministic finite automaton 确定型有穷自动机),另一种是 NFA(NFA Non-deterministic finite automaton 非确定型有穷自动机)。NFA 速度较 DFA 更慢,并且实现复杂,但是它又有着比 DFA 强大的多的功能,比如支持反向引用等。像 javaScript、java、php、python、c#等语言的正则引擎都是 NFA 型,NFA 正则引擎的实现过程中使用了回溯。
3.2.1 没有回溯的正则
举一个网上常见的例子,正则表达式/ab{1,3}c/g 去匹配文本'abbc',我们接下来会通过 RegexBuddy 分析其中的匹配过程,后续的一个章节有关于 RegexBuddy 的使用介绍。
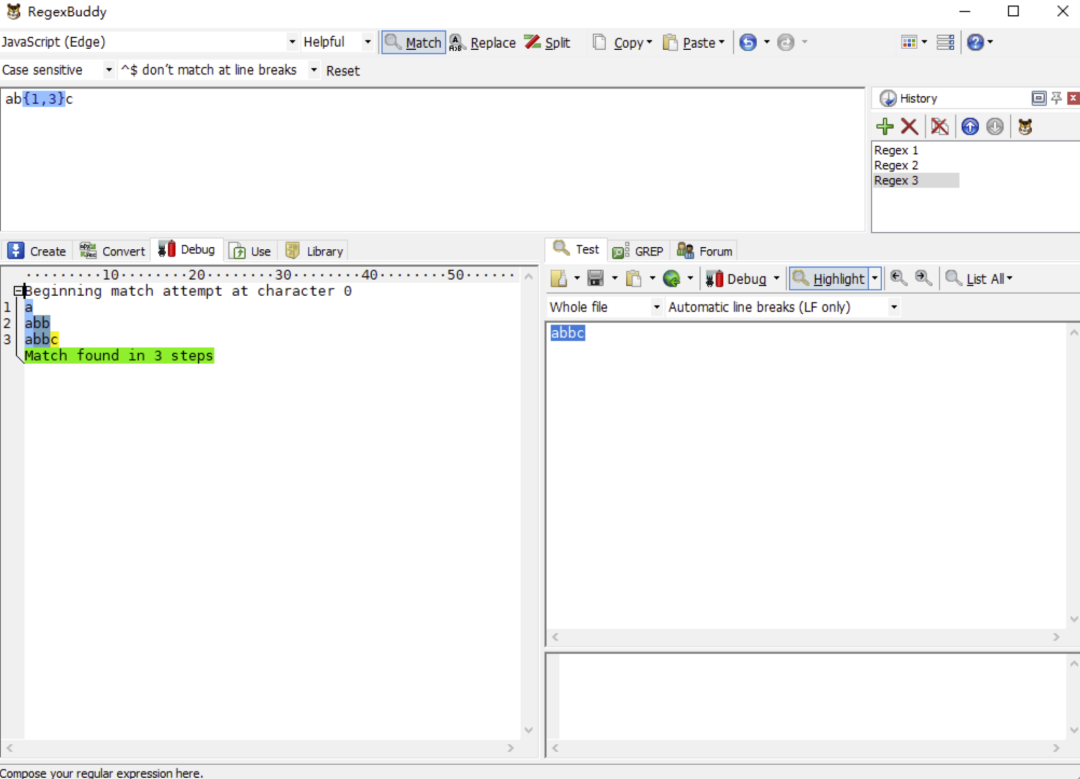
如上图所示,让我们一步一步分解匹配过程:
- 正则引擎先匹配 a。
- 正则引擎尽可能多地(贪婪)匹配 b。
- 正则引擎匹配 c,完成匹配。
在这之中,匹配过程都很顺利,并没发生意外(回溯)。
3.2.2 有正则回溯的正则
让我们把上面的正则修改一下,/ab{1,3}c/g 改成/ab{1,3}bc/g,接下再通过 RegexBuddy 查看分析结果。
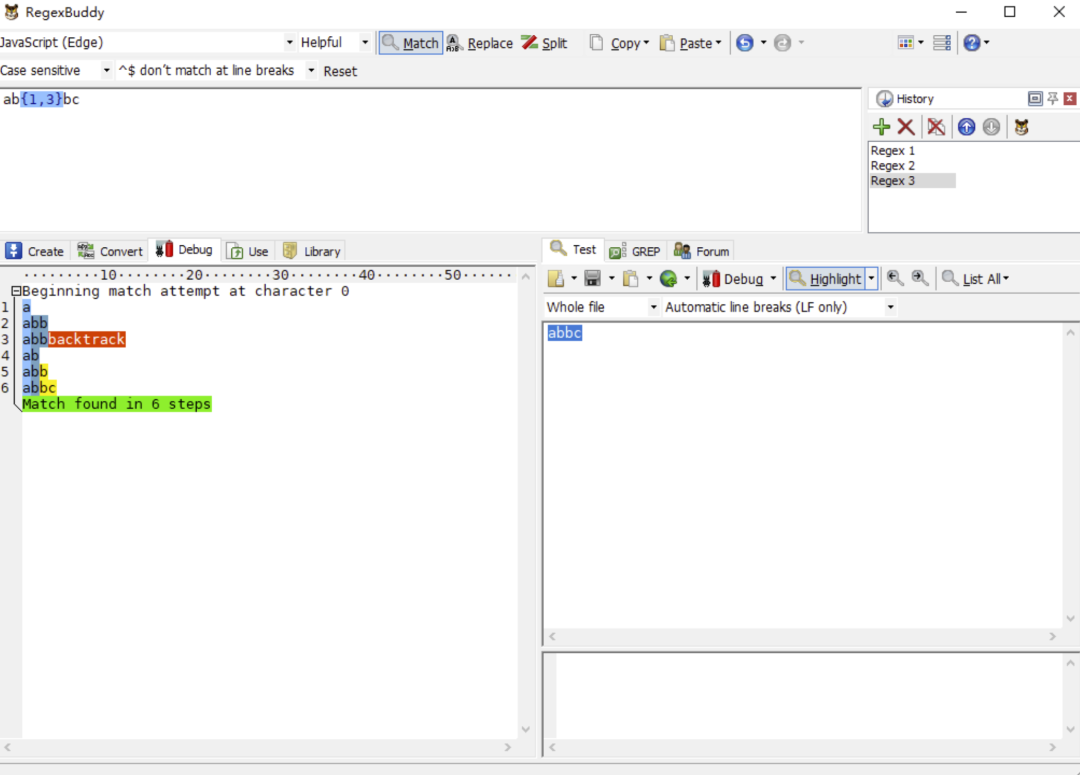
我们再一步一步分解匹配过程:
- 正则引擎先匹配 a。
- 正则引擎尽可能多地(贪婪)匹配 b{1,3}中的 b。
- 正则引擎去匹配 b,发现没 b 了,糟糕!赶紧回溯!
- 返回 b{1,3}这一步,不能这么贪婪,少匹配个 b。
- 正则引擎去匹配 b。
- 正则引擎去匹配 c,完成匹配。
以上,就是一个简单的回溯过程。
3.3 正则回溯的几种常见形式
从上面发生正则回溯的例子可以看出来,正则回溯的过程就是一个试错的过程,这也是回溯算法的精髓所在。回溯会增加匹配的步骤,势必会影响文本匹配的性能,所以,要想提升正则表达式的匹配性能,了解回溯出现的场景(形式)是非常关键的。
3.3.1 贪婪量词
在 NFA 正则引擎中,量词默认都是贪婪的。当正则表达式中使用了下表所示的量词,正则引擎一开始会尽可能贪婪的去匹配满足量词的文本。当遇到匹配不下去的情况,就会发生回溯,不断试错,直至失败或者成功。
量词说明a*0 or morea+1 or morea?0 or 1a{5}exactly fivea{2,}two or morea{1,3}between one & three
当多个贪婪量词挨着存在,并相互有冲突时,秉持的是"先到先得"的原则,如下所示:
- let string = "12345";
- let regex = /(\d{1,3})(\d{1,3})/;
- console.log( string.match(regex) );
- // => ["12345", "123", "45", index: 0, input: "12345"]
3.3.2 惰性量词
贪婪是导致回溯的重要原因,那我们尽量以懒惰匹配的方式去匹配文本,是否就能避免回溯了呢?答案是否定的。
让我们还是看回最初的例子,/ab{1,3}c/g 去匹配 abbc。接下来,我们再把正则修改一下,改成/ab{1,3}?c/g 去匹配 abbc,以懒惰匹配的方式去匹配文本,RegexBuddy 执行步骤如下图所示:
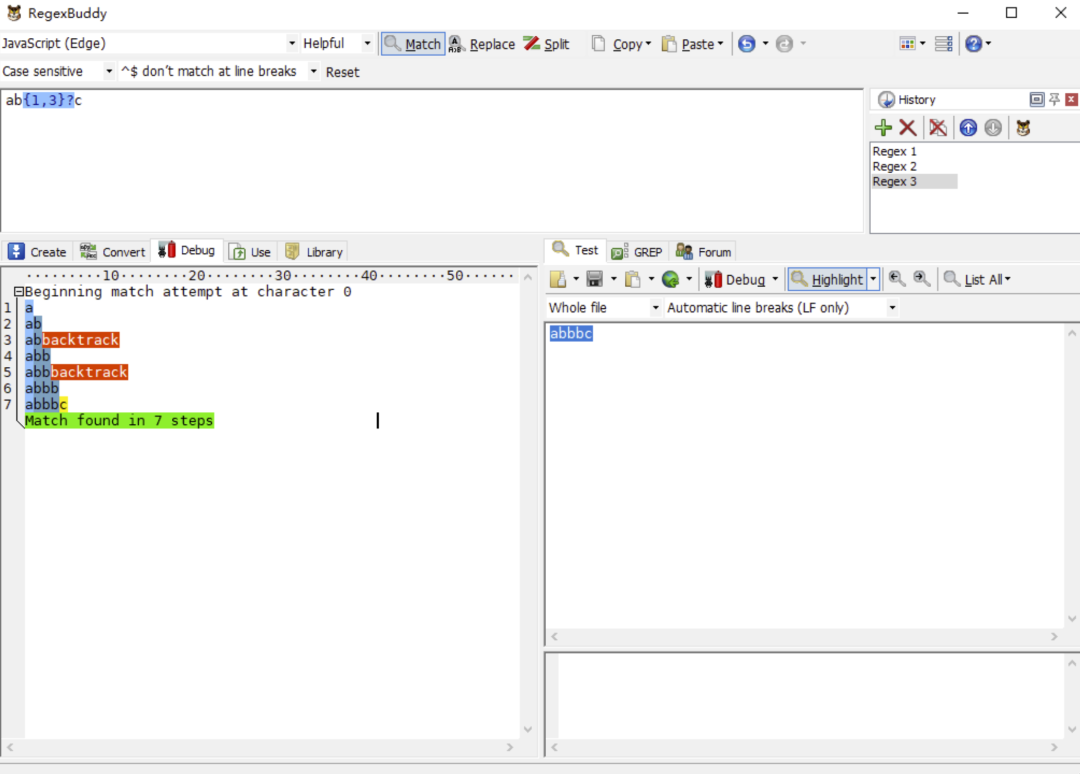
- 正则引擎先匹配 a。
- 正则引擎尽可能少地(懒惰)匹配 b{1,3}中的 b。
- 正则引擎去匹配 c,糟糕!怎么有个 b 挡着,匹配不了 c 啊!赶紧回溯!
- 返回 b{1,3}这一步,不能这么懒惰,多匹配个 b。
- 正则引擎再去匹配 c,糟糕!怎么还有 b 挡着,匹配不了 c 啊!赶紧回溯!
- 返回 b{1,3}这一步,不能这么懒惰,再多匹配个 b。
- 正则引擎再去匹配 c,匹配成功,棒棒哒!
本来是好端端不会发生回溯的正则,因为使用了惰性量词进行懒惰匹配后,反而产生了回溯了。所以说,惰性量词也不能瞎用,关键还是要看场景。
3.3.3 分组
分支的匹配规则是:按照分支的顺序逐个匹配,当前面的分支满足要求了,则舍弃后面的分支。
举个简单的分支栗子,使用正则表达式去匹配 /abcde|abc/g 文本 abcd,还是通过 RegexBuddy 查看执行步骤:
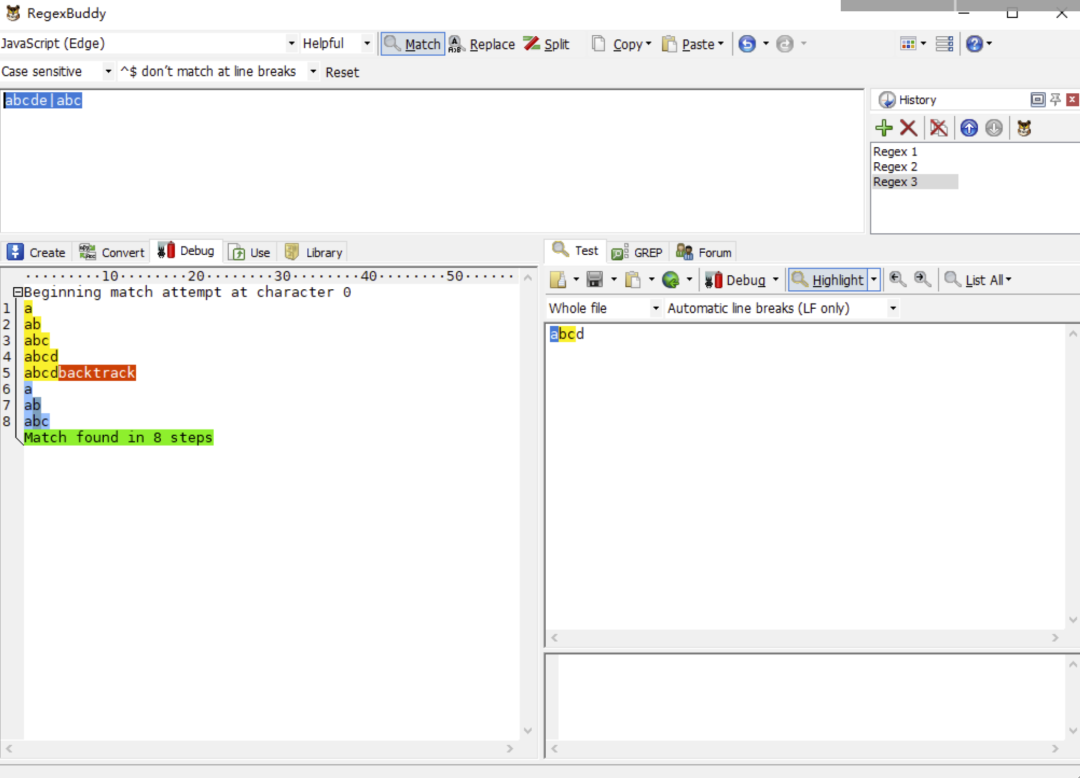
- 正则引擎匹配 a。
- 正则引擎匹配 b。
- 正则引擎匹配 c。
- 正则引擎匹配 d。
- 正则引擎匹配 e,糟糕!下一个并不是 e,赶紧回溯!
- 上一个分支走不通,切换分支,第二个分支正则引擎匹配 a。
- 第二个分支正则引擎匹配 b。
- 第二个分支正则引擎匹配 c,匹配成功!
由此,可以看出,分组匹配的过程,也是个试错的过程,中间是可能产生回溯的。
4. 正则的分析与调试
RegexBuddy 是个十分强大的正则表达式学习、分析及调试工具。RegexBuddy 支持 C++、Java、JavaScript、Python 等十几种主流编程语言。通过 RegexBuddy,能看到正则一步步创建的过程。结合测试文本,你能看到正则一步步执行匹配的过程,这对于理解正则回溯和对正则进行进一步优化,都有极大的帮助。
4.1 安装分析调试工具
可以在 RegexBuddy 的官方网站下载及获取 RegexBuddy。
下载完后,一步步点击安装即可。
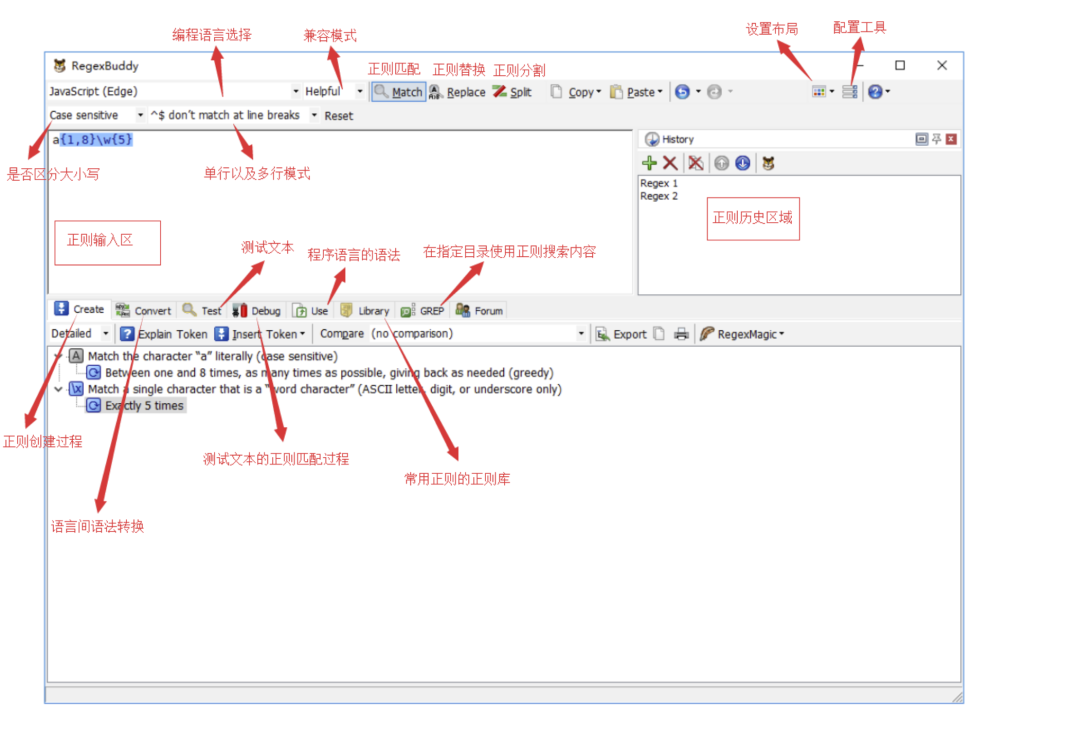
4.2 工具界面介绍
下图便是 RegexBuddy 界面的各个面板及相关功能。
4.3 创建正则
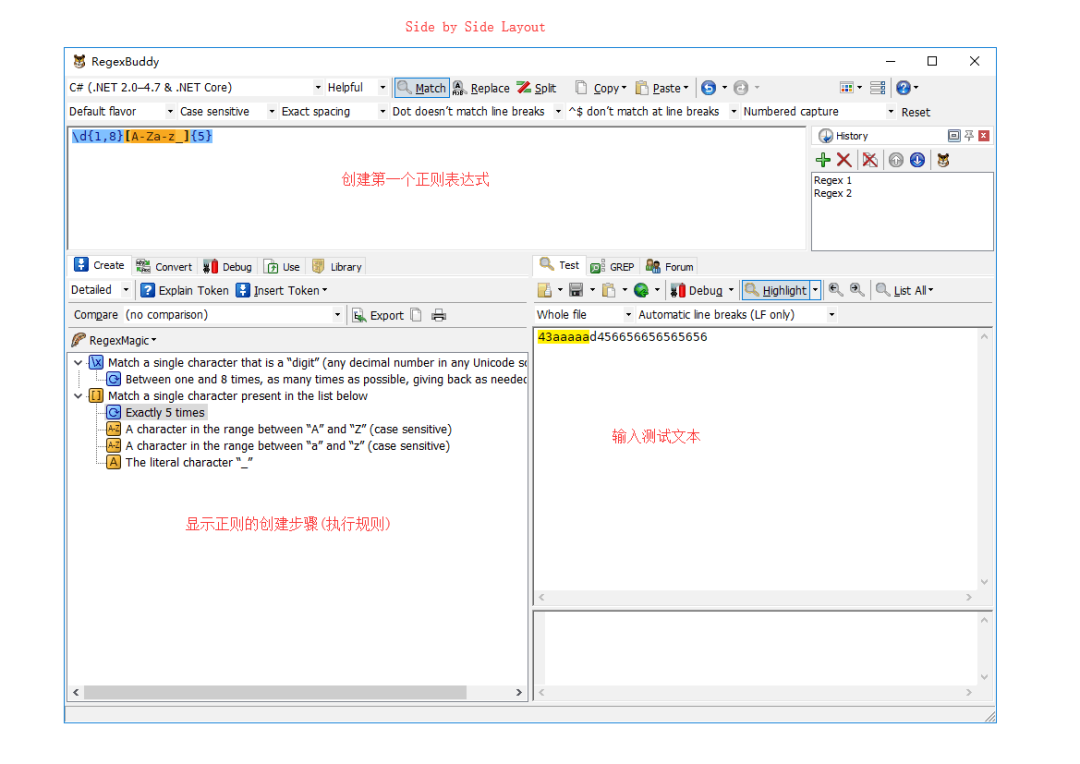
为了方便使用,可以在布局设置那里将布局设置成 Side by Side Layout。
在正则输入区输入你的正则 regex1,查看 Create 面板,就会发现面板上显示了正则的创建过程(或者说是匹配规则),在 Test 面板区域输入你的测试文本,满足 regex1 匹配规则的部分会高亮显示,如下图所示。
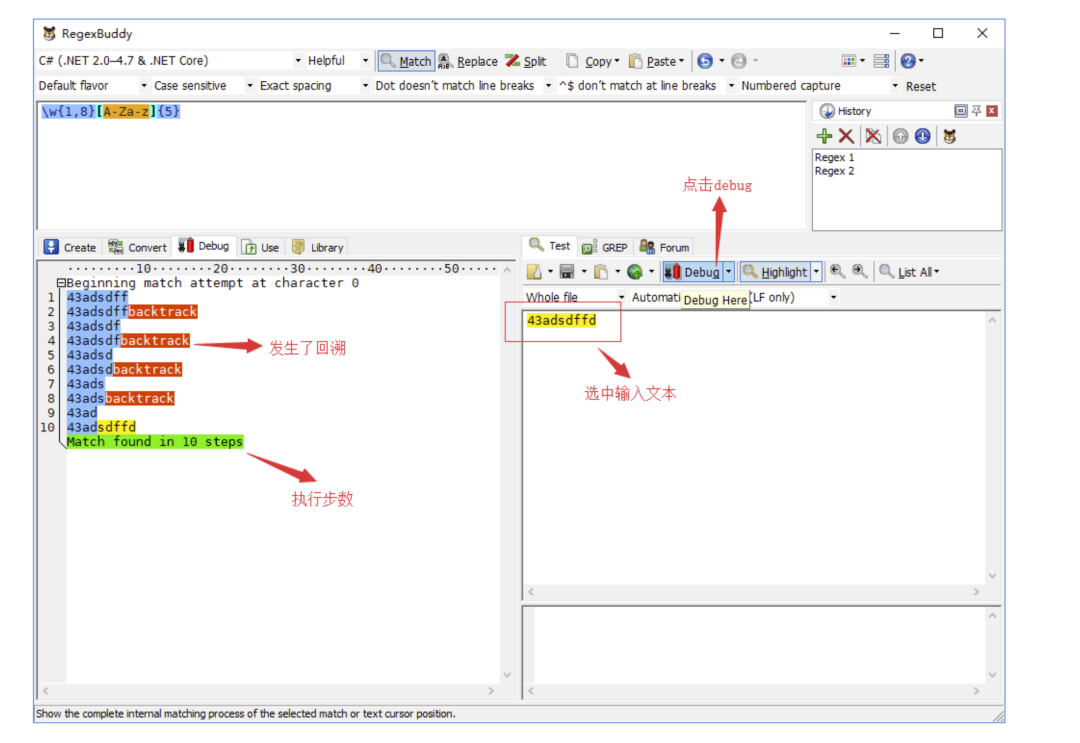
4.4 使用 RegexBuddy 的 Debug 功能
选中测试文本,点击 debug 就可以进入 RegexBuddy 的 debug 模式,个人觉得这是 RegexBuddy 最强大地方,因为它可以让你清楚地知道你输入的正则对测试文本的匹配过程,执行了多少步,哪里发生了回溯,哪里需要优化,你都能一目了然。
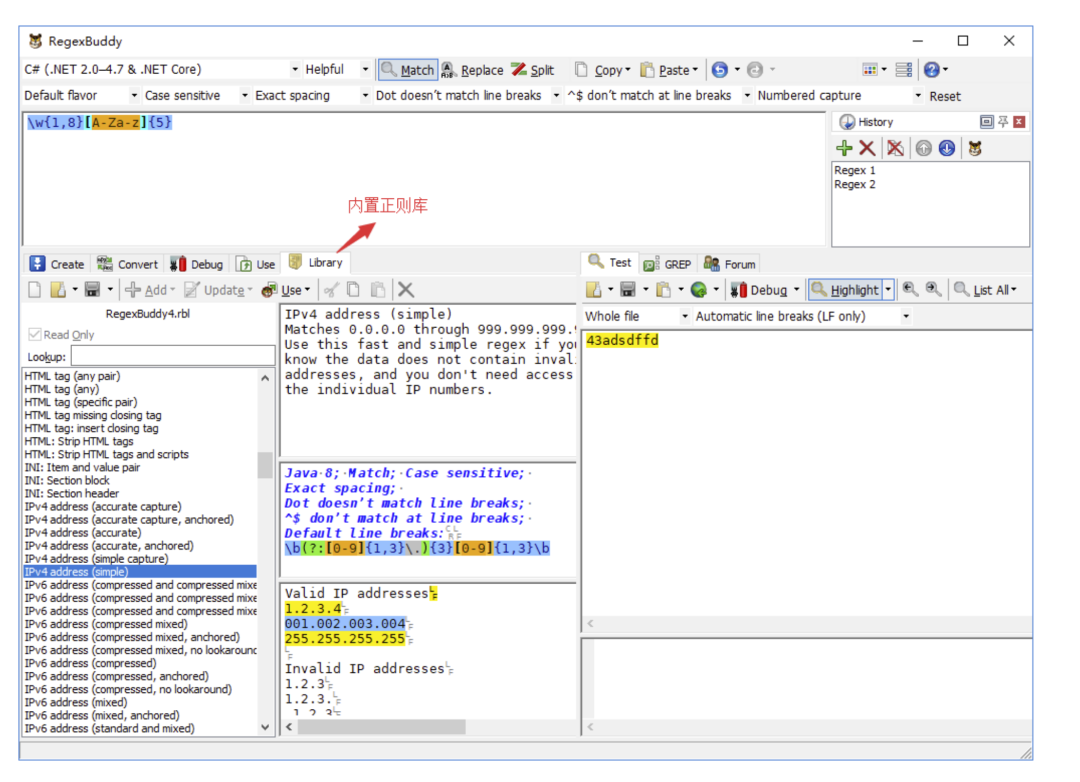
4.5 使用 RegexBuddy 的 Library 功能
RegexBuddy 的正则库内置了很多常用正则,日常编码过程中需要的很多正则表达式都能在该正则库中找到。
4.6 更多工具推荐
- 正则可视化-regexper
- 正则可视化-regulex
- 正则在线调试
5. 正则性能优化
正则是个很好用的利器,如果使用得当,如有神助,能省掉大量代码。当如果使用不当,则是处处埋坑。所以,本章节的重点就是总结如何写一个高性能的正则表达式。
5.1 避免量词嵌套
举个简单的例子对比:
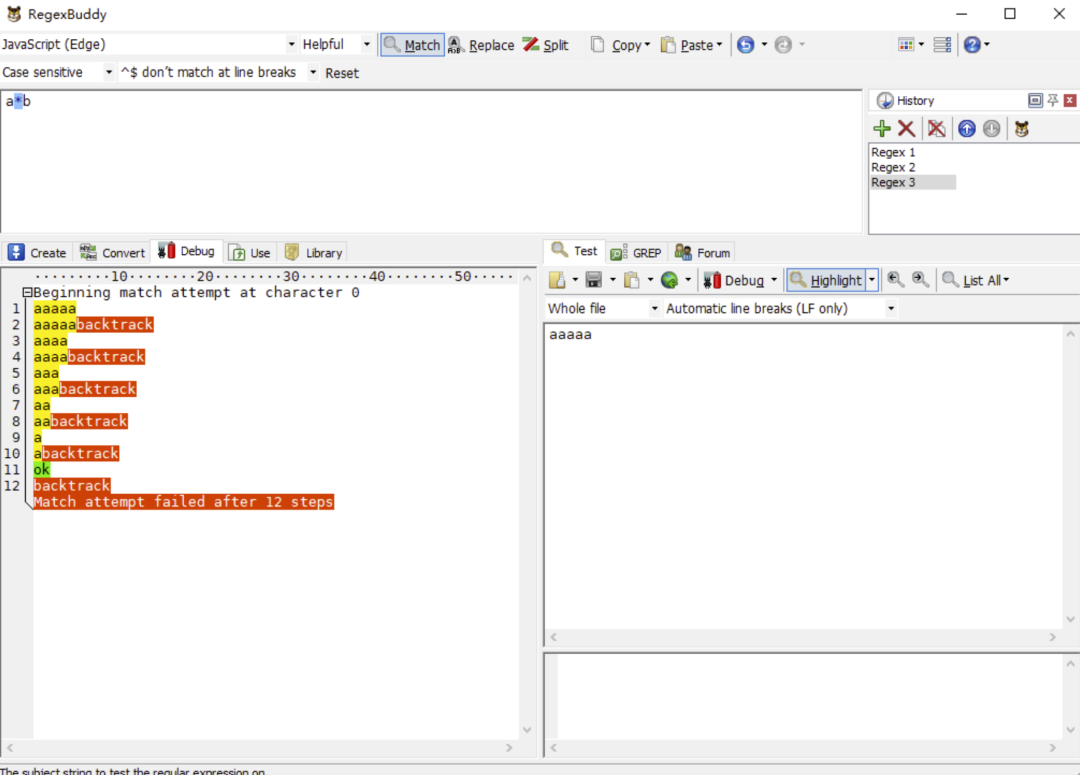
我们使用正则表达式/a*b/去匹配字符串 aaaaa,看下图 RegexBuddy 的执行过程:
我们将以上正则修改成/(a*)*b/去匹配字符串 aaaaa,再看看 RegexBuddy 的执行结果过程:
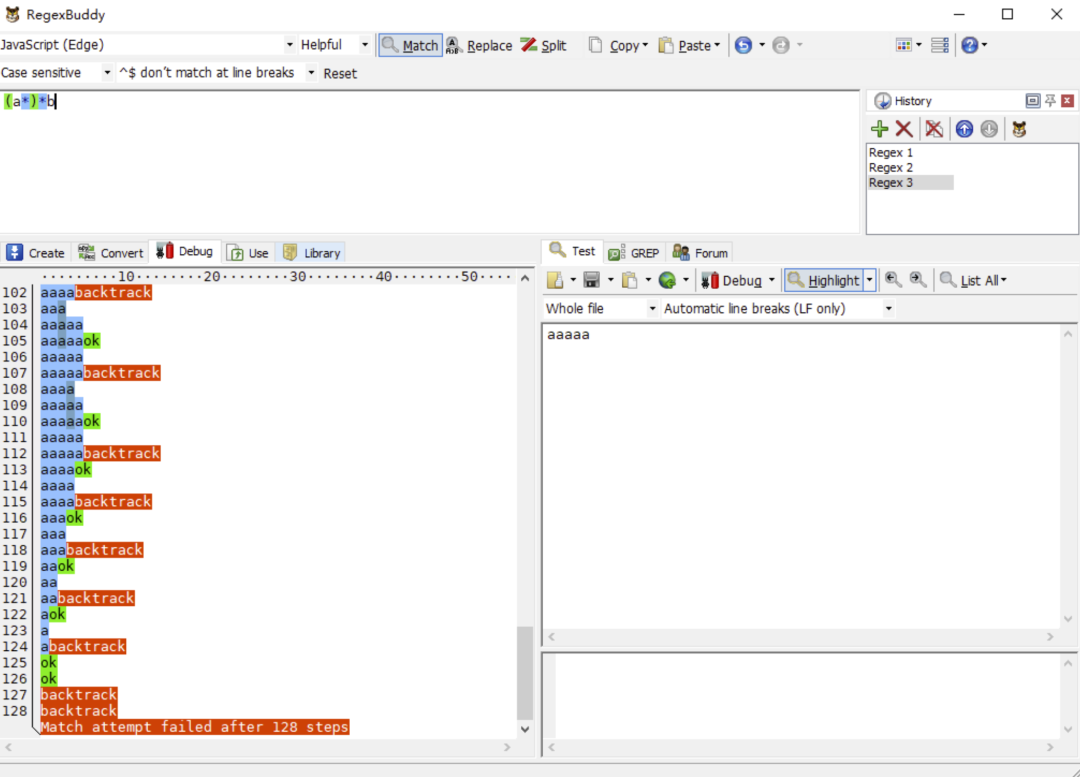
以上两个正则的基本执行步骤可以简单认为是:
- 贪婪匹配
- 回溯
- 直至发现匹配失败
但令人惊奇的是,第一个正则的从开始匹配到匹配失败这个过程只有 14 步。而第二个正则却有 128 步之多。可想而知,嵌套量词会大大增加正则的执行过程。因为这其中进行了两层回溯,这个执行步骤增加的过程就如同算法复杂度从 O(n)上升到 O(n^2)的过程一般。
所以,面对量词嵌套,我们需作出适当的转化消除这些嵌套:
- (a*)* <=> (a+)* <=> (a*)+ <=> a*
- (a+)+ <=> a+
5.2 使用非捕获组
NFA 正则引擎中的括号主要有两个作用:
- 主流功能,提升括号中内容的运算优先级
- 反向引用
反向引用这个功能很强大,强大的代价是消耗性能。所以,当我们如果不需要用到括号反向引用的功能时,我们应该尽量使用非捕获组,也就是:
- // 捕获组与非捕获组
- () => (?:)
5.3 分支优化
分支也是导致正则回溯的重要原因,所以,针对正则分支,我们也需要作出必要的优化。
5.3.1 减少分支数量
首先,需要减少分支数量。比如不少正则在匹配 http 和 https 的时候喜欢写成:
- /^http|https/
其实上面完全可以优化成:
- /^https?/
这样就能减少没必要的分支回溯
5.3.2 缩小分支内的内容
缩小分支中的内容也是很有必要的,例如我们需要匹配 this 和 that ,我们也许会写成:
- /this|that/
但上面其实完全可以优化成
- /th(?:is|at)/
有人可能认为以上没啥区别,实践出真知,让我们用以上两个正则表达式去匹配一下 that。
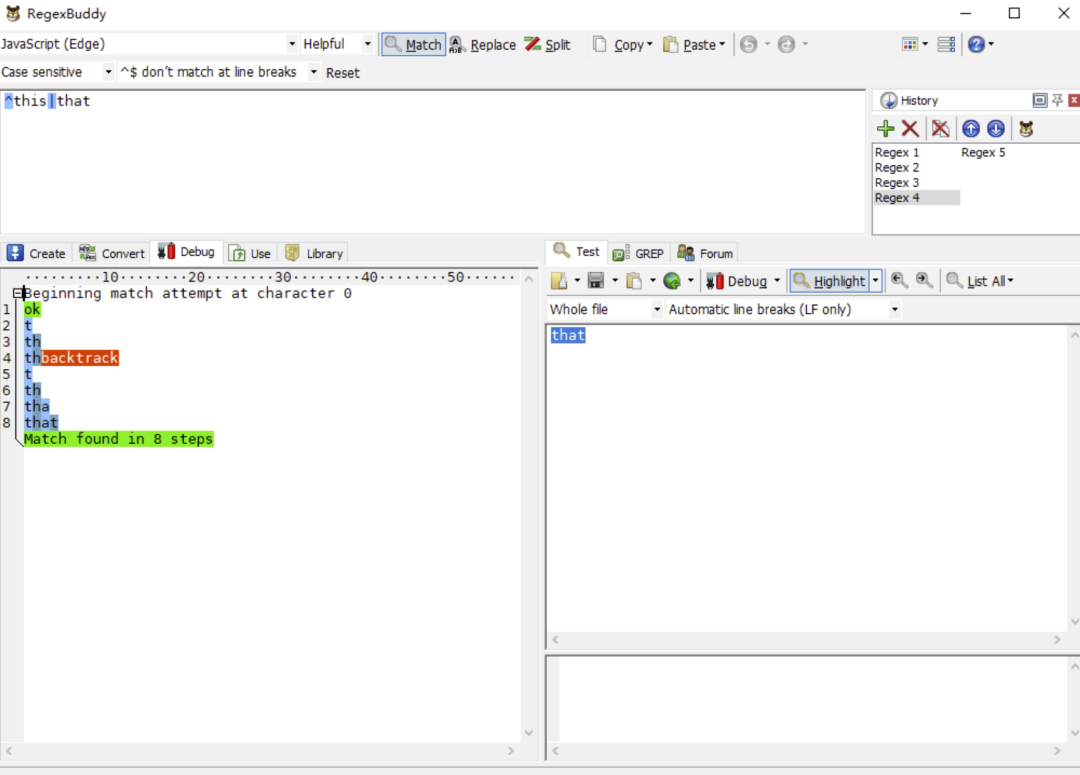
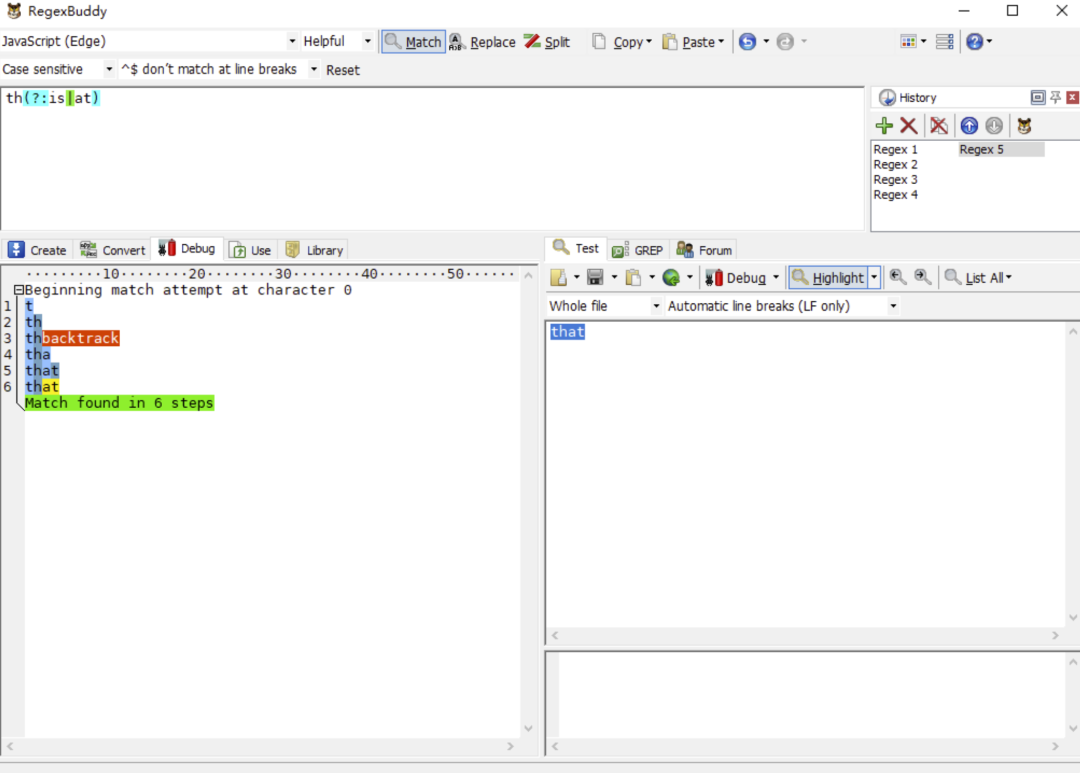
我们会发现第一个正则的执行步骤比第一个正则多两步,那是因为第一个正则的回溯路径比第二个正则的回溯路径更长了,最终导致执行步骤变长。
5.4 锚点优化
在能使用锚点的情况下尽量使用锚点。大部分正则引擎会在编译阶段做些额外分析, 判断是否存在成功匹配必须的字符或者字符串。类似^、$ 这类锚点匹配能给正则引擎更多的优化信息。
例如正则表达式 hello(hi)?$ 在匹配过程中只可能从字符串末尾倒数第 7 个字符开始, 所以正则引擎能够分析跳到那个位置, 略过目标字符串中许多可能的字符, 大大提升匹配速度。
6. 结语
曾经有一次因为写一个性能恶劣的正则表达式,导致代码执行过程因为性能问题挂掉。于是下定决心要把正则表达式搞明白,看了不少文章书籍,做了不少练习之后,总算摸到了些门道,也真真切切体会到正则表达式的优美和强大。写下此文,记录下一些学习心得和总结,望批评指正,共同进步。
7. 参考
- 正则表达式中的悲观回溯
- 小心别落入正则回溯陷阱
- 正则匹配原理解析
- learncodethehardway
- 正则表达式系列总结
- wikipedia Backtracking
- 精通正则表达式