如果两个变量有共变关系,我们就可以用其中一个变量来预测另外一个变量的走势,如果这种共变关系是一种因果关系,我们就可以在统计分析中对其进行控制。
有点不好理解,所以今天给大家准备了实例,并且用图形给大家说明这个问题。
实例操练
今天用的数据依然是R自带的diamonds数据集,数据变量什么意思请大家自行百度。
在上一篇文章中,我们用箱型图画出不同的cut上钻石价格的分布如下图
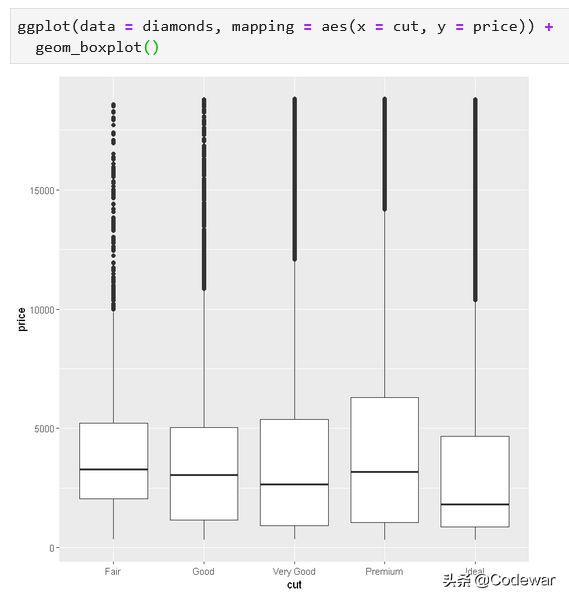
在上面的图中我们可以看到随着钻石的cut越好,似乎钻石的价格越低,这个关系明显是不符合常理的,值得探讨一下。
其实探讨cut、price之间的关系是挺复杂的一个事情,因为cut和carat, carat和price之间都有紧密的关系,所以我们现在的思路就是说,希望能够在去除了carat对price的效应之后,再看cut和price的关系。
下面的代码建立了carat和price的模型,并且计算了模型的残差(就是预测值和实际值的区别),残差就反映了因变量未被自变量解释的部分,在本例中就是price的变异中carat解释不了的部分。
- library(modelr)
- mod <- lm(log(price) ~ log(carat), data = diamonds)
- diamonds2 <- diamonds %>% add_residuals(mod) %>%
- mutate(resid = exp(resid))
- ggplot(data = diamonds2) + geom_point(mapping = aes(x = carat, y = resid))
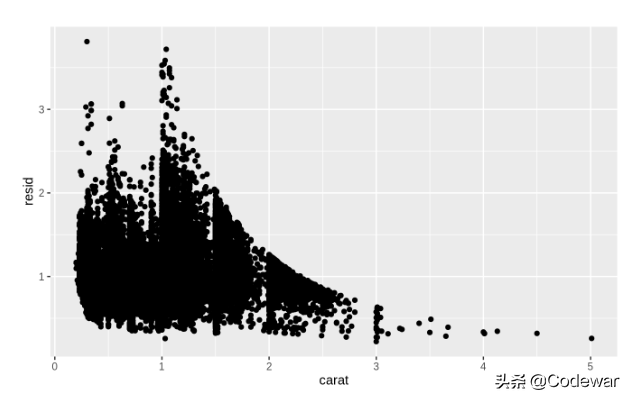
上面的代码同时还做出了carat与模型残差的散点图,可以看出只用carat来解释price是不太好的。
那么抠掉了carat和price的关系之后,怎么看cut和price的关系呢?代码如下:
- ggplot(data = diamonds2) +
- geom_boxplot(mapping = aes(x = cut, y = resid))
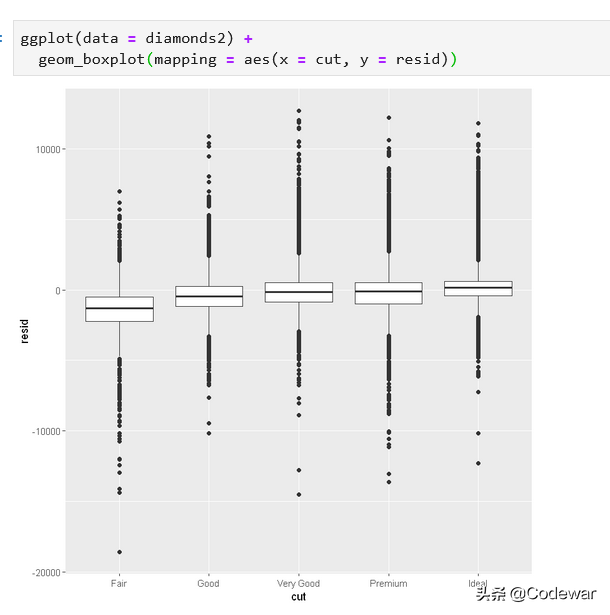
这个时候我们是用cut为自变量,残差为因变量进行了作图,也就是看一看抠掉了carat对price的效应后,cut对price的实际的关系,可以看到这回随着cut越来越好,price也愈来愈高,这下就对了。
实际上,上面的过程就是一个统计控制的过程,我们在看cut对price的关系的时候需要控制掉carat对price的关系,这样得到的结果才是纯净的结果,有兴趣的同学还可以去看一看控制变量和混杂变量的区别,嘿嘿。
小结
今天用一个实际的例子给大家写了统计控制,感谢大家耐心看完。发表这些东西的主要目的就是督促自己,希望大家关注评论指出不足,一起进步。内容我都会写的很细,用到的数据集也会在原文中给出链接,你只要按照文章中的代码自己也可以做出一样的结果,一个目的就是零基础也能懂,因为自己就是什么基础没有从零学Python和R的,加油。