450，什么叫回溯算法，一看就会，一写就废-回溯算法是什么

什么叫回溯算法

对于回溯算法的定义，百度百科上是这样描述的：回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

看明白没，回溯算法其实就是一个不断探索尝试的过程，探索成功了也就成功了，探索失败了就在退一步，继续尝试……，

组合总和

组合总和算是一道比较经典的回溯算法题，其中有一道题是这样的。

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。
解集不能包含重复的组合。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

这题说的很明白，就是从1-9中选出k个数字，他们的和等于n，并且这k个数字不能有重复的。所以第一次选择的时候可以从这9个数字中任选一个，沿着这个分支走下去，第二次选择的时候还可以从这9个数字中任选一个，但因为不能有重复的，所以要排除第一次选择的，第二次选择的时候只能从剩下的8个数字中选一个……。这个选择的过程就比较明朗了，我们可以把它看做一棵9叉树，除叶子结点外每个节点都有9个子节点，也就是下面这样

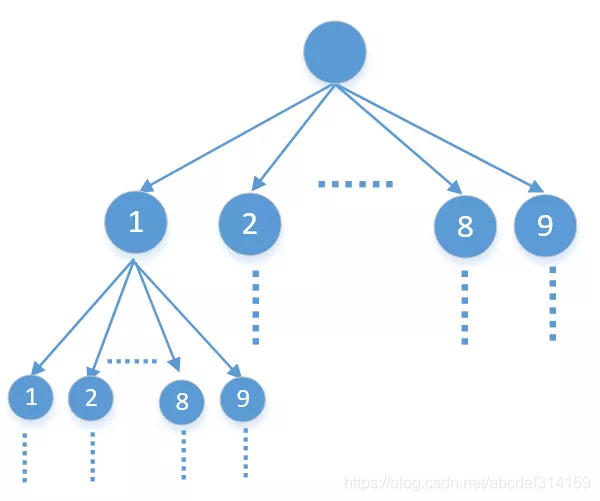
从9个数字中任选一个，就是沿着他的任一个分支一直走下去，其实就是DFS(如果不懂DFS的可以看下373，数据结构-6,树)，二叉树的DFS代码是下面这样的

public static void treeDFS(TreeNode root) { 
    if (root == null) 
        return; 
    System.out.println(root.val); 
    treeDFS(root.left);    treeDFS(root.right);}

这里可以仿照二叉树的DFS来写一下9叉树，9叉树的DFS就是通过递归遍历他的9个子节点，代码如下

public static void treeDFS(TreeNode root) { 
    //递归必须要有终止条件 
    if (root == null) 
        return; 
    System.out.println(root.val);    //通过循环，分别遍历9个子树 
    for (int i = 1; i <= 9; i++) { 
        //2，一些操作，可有可无，视情况而定 
        treeDFS("第i个子节点"); 
        //3，一些操作，可有可无，视情况而定 
    }}

DFS其实就相当于遍历他的所有分支，就是列出他所有的可能结果，只要判断结果等于n就是我们要找的，那么这棵9叉树最多有多少层呢，因为有k个数字，所以最多只能有k层。来看下代码

public List<List<Integer>> combinationSum3(int k, int n) { 
    List<List<Integer>> res = new ArrayList<>(); 
    dfs(res, new ArrayList<>(), k, 1, n); 
    return res; 
}private void dfs(List<List<Integer>> res, List<Integer> list, int k, int start, int n) { 
    //终止条件，如果满足这个条件，再往下找也没什么意义了 
    if (list.size() == k || n <= 0) { 
        //如果找到一组合适的就把他加入到集合list中 
        if (list.size() == k && n == 0) 
            res.add(new ArrayList<>(list)); 
        return; 
    } 
    //通过循环，分别遍历9个子树 
    for (int i = start; i <= 9; i++) { 
        //选择当前值 
        list.add(i); 
        //递归 
        dfs(res, list, k, i + 1, n - i); 
        //撤销选择 
        list.remove(list.size() - 1); 
    } 
}

代码相对来说还是比较简单的，我们来分析下(如果看懂了可以直接跳过)。

代码dfs中最开始的地方是终止条件的判断，之前在426，什么是递归，通过这篇文章，让你彻底搞懂递归中讲过，递归必须要有终止条件。
下面的for循环分别遍历他的9个子节点，注意这里的i是从start开始的，所以有可能还没有9个子树，前面说过，如果从9个数字中选择一个之后，第2次就只能从剩下的8个选择了，第3次就只能从剩下的7个中选择了……
在第20行dsf中的start是i+1，这里要说一下为什么是i+1。比如我选择了3，下次就应该从4开始选择，如果不加1，下次还从3开始就出现了数字重复，明显与题中的要求不符
for循环的i为什么不能每次都从1开始，如果每次都从1开始就会出现结果重复，比如选择了[1，2]，下次可能就会选择[2，1]。
如果对回溯算法不懂的，可能最不容易理解的就是最后一行，为什么要撤销选择。如果经常看我公众号的同学可能知道，也就是我经常提到的分支污染问题，因为list是引用传递，当从一个分支跳到另一个分支的时候，如果不把前一个分支的数据给移除掉，那么list就会把前一个分支的数据带到下一个分支去，造成结果错误(下面会讲)。那么除了把前一个分支的数据给移除以外还有一种方式就是每个分支都创建一个list，这样每个分支都是一个新的list，都不互相干扰，也就是下面图中这样

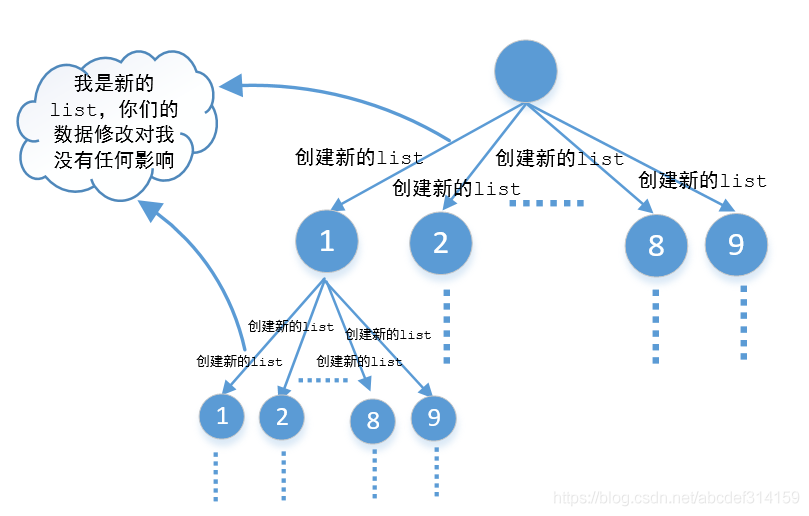
代码如下

public List<List<Integer>> combinationSum3(int k, int n) { 
    List<List<Integer>> res = new ArrayList<>(); 
    dfs(res, new ArrayList<>(), k, 1, n); 
    return res; 
}private void dfs(List<List<Integer>> res, List<Integer> list, int k, int start, int n) { 
    //终止条件，如果满足这个条件，再往下找也没什么意义了 
    if (list.size() == k || n <= 0) { 
        //如果找到一组合适的就把他加入到集合list中 
        if (list.size() == k && n == 0) 
            res.add(new ArrayList<>(list)); 
        return; 
    } 
    //通过循环，分别遍历9个子树 
    for (int i = start; i <= 9; i++) { 
        //创建一个新的list，和原来的list撇清关系，对当前list的修改并不会影响到之前的list 
        List<Integer> subList = new LinkedList<>(list); 
        subList.add(i); 
        //递归 
        dfs(res, subList, k, i + 1, n - i); 
        //注意这里没有撤销的操作，因为是在一个新的list中的修改，原来的list并没有修改， 
        //所以不需要撤销操作 
    } 
}

我们看到最后并没有撤销的操作，这是因为每个分支都是一个新的list，你对当前分支的修改并不会影响到其他分支，所以并不需要撤销操作。

注意：大家尽量不要写这样的代码，这种方式虽然也能解决，但每个分支都会重新创建list，效率很差。

要搞懂最后一行代码首先要明白什么是递归，递归分为递和归两部分，递就是往下传递，归就是往回走。递归你从什么地方调用最终还会回到什么地方去，我们来画个简单的图看一下

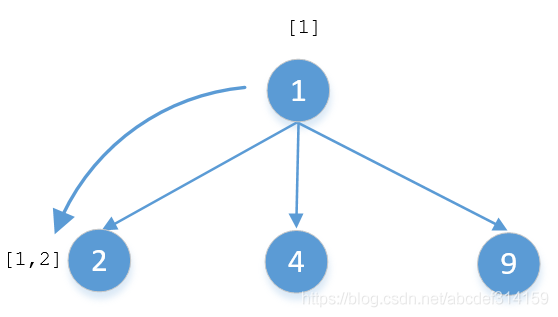
这是一棵非常简单的3叉树，假如要对他进行DFS遍历，当沿着1→2这条路径走下去的时候，list中应该是[1，2]。因为是递归调用最终还会回到节点1，如果不把2给移除掉，当沿着1→4这个分支走下去的时候就变成[1，2，4]，但实际上1→4这个分支的结果应该是[1，4]，这是因为我们把前一个分支的值给带过来了。当1，2这两个节点遍历完之后最终还是返回节点1，在回到节点1的时候就应该把结点2的值给移除掉，让list变为[1]，然后再沿着1→4这个分支走下去，结果就是[1，4]。

我们来总结一下回溯算法的代码模板吧

private void backtrack("原始参数") { 
    //终止条件(递归必须要有终止条件) 
    if ("终止条件") { 
        //一些逻辑操作（可有可无，视情况而定） 
        return; 
    }    for (int i = "for循环开始的参数"; i < "for循环结束的参数"; i++) { 
        //一些逻辑操作（可有可无，视情况而定） 
        //做出选择 
        //递归 
        backtrack("新的参数"); 
        //一些逻辑操作（可有可无，视情况而定） 
        //撤销选择 
    } 
}

有了模板，回溯算法的代码就非常容易写了，下面就根据模板来写几个经典回溯案例的答案。

八皇后问题

八皇后问题也是一道非常经典的回溯算法题，前面也有对八皇后问题的专门介绍，有不明白的可以先看下394，经典的八皇后问题和N皇后问题。他就是不断的尝试，如果当前位置能放皇后就放，一直到最后一行如果也能放就表示成功了，如果某一个位置不能放，就回到上一步重新尝试。比如我们先在第1行第1列放一个皇后，如下图所示

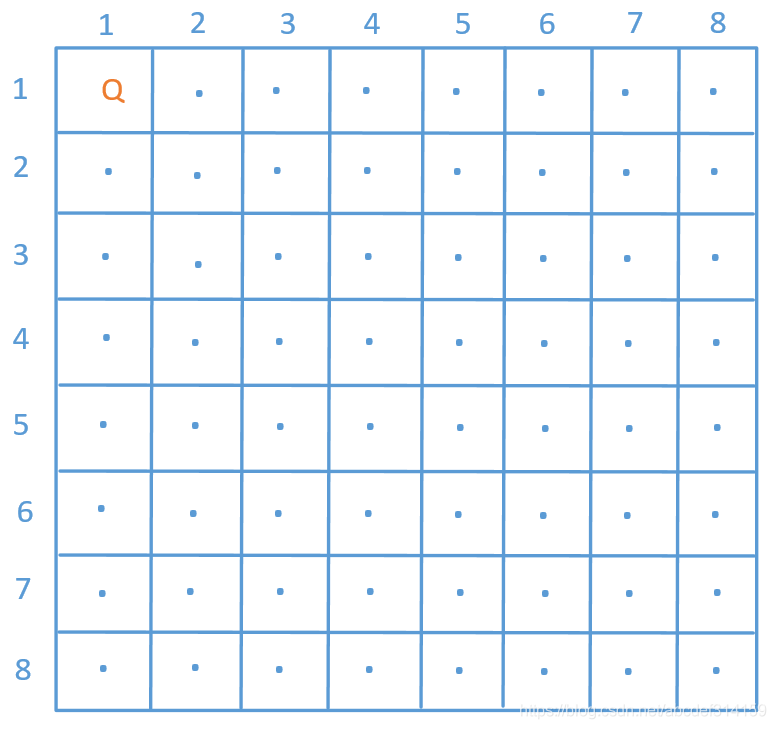
然后第2行从第1列开始在不冲突的位置再放一个皇后，然后第3行……一直这样放下去，如果能放到第8行还不冲突说明成功了，如果没到第8行的时候出现了冲突就回到上一步继续查找合适的位置……来看下代码

//row表示的是第几行 
public void solve(char[][] chess, int row) { 
    //终止条件，row是从0开始的，最后一行都可以放，说明成功了    if (row == chess.length) {        //自己写的一个公共方法，打印二维数组的，        //主要用于测试数据用的        Util.printTwoCharArrays(chess);        System.out.println();        return;    }    for (int col = 0; col < chess.length; col++) { 
        //验证当前位置是否可以放皇后 
        if (valid(chess, row, col)) { 
            //如果在当前位置放一个皇后不冲突， 
            //就在当前位置放一个皇后 
            chess[row][col] = 'Q'; 
            //递归，在下一行继续…… 
            solve(chess, row + 1); 
            //撤销当前位置的皇后 
            chess[row][col] = '.'; 
        } 
    } 
}

全排列问题

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:
输入: [1,2,3]
输出:

[  
[1,2,3],  
[1,3,2],  
[2,1,3],  
[2,3,1],  
[3,1,2],  
[3,2,1]  
]

这道题我们可以把它当做一棵3叉树，所以每一步都会有3种选择，具体过程就不在分析了，直接根据上面的模板来写下代码

public List<List<Integer>> permute(int[] nums) { 
    List<List<Integer>> list = new ArrayList<>(); 
    backtrack(list, new ArrayList<>(), nums); 
    return list; 
}private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums) { 
    //终止条件 
    if (tempList.size() == nums.length) { 
        //说明找到一一组组合 
        list.add(new ArrayList<>(tempList)); 
        return; 
    } 
    for (int i = 0; i < nums.length; i++) { 
        //因为不能有重复的，所以有重复的就不能选 
        if (tempList.contains(nums[i])) 
            continue; 
        //选择当前值 
        tempList.add(nums[i]); 
        //递归 
        backtrack(list, tempList, nums); 
        //撤销选择 
        tempList.remove(tempList.size() - 1); 
    } 
}

是不是感觉很简单。

子集问题

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集(幂集)。

说明：解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:

输入: nums = [1,2,3] 
输出: 
[ 
[3], 
[1], 
[2], 
[1,2,3], 
[1,3], 
[2,3], 
[1,2], 
[] 
]

我们还是根据模板来修改吧

public List<List<Integer>> subsets(int[] nums) { 
    List<List<Integer>> list = new ArrayList<>(); 
    //先排序 
    Arrays.sort(nums); 
    backtrack(list, new ArrayList<>(), nums, 0); 
    return list; 
} 
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums, int start) { 
    //注意这里没有写终止条件，不是说递归一定要有终止条件的吗，这里怎么没写，其实这里的终止条件 
    //隐含在for循环中了，当然我们也可以写if(start>nums.length) rerurn;只不过这里省略了。 
    list.add(new ArrayList<>(tempList)); 
    for (int i = start; i < nums.length; i++) { 
        //做出选择 
        tempList.add(nums[i]); 
        //递归 
        backtrack(list, tempList, nums, i + 1); 
        //撤销选择 
        tempList.remove(tempList.size() - 1); 
    } 
}

所以类似这种题基本上也就是这个套路，就是先做出选择，然后递归，最后再撤销选择。在讲第一道示例的时候提到过撤销的原因是防止把前一个分支的结果带到下一个分支造成结果错误。不过他们不同的是，一个是终止条件的判断，还一个就是for循环的起始值，这些都要具体问题具体分析。下面再来看最后一到题解数独。

解数独

数独大家都玩过吧，他的规则是这样的

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

过程就不在分析了，直接看代码，代码中也有详细的注释，这篇讲的是回溯算法，这里主要看一下backTrace方法即可，其他的可以先不用看

//回溯算法 
public static boolean solveSudoku(char[][] board) { 
    return backTrace(board, 0, 0); 
}//注意这里的参数，row表示第几行，col表示第几列。private static boolean backTrace(char[][] board, int row, int col) { 
    //注意row是从0开始的，当row等于board.length的时候表示数独的 
    //最后一行全部读遍历完了，说明数独中的值是有效的，直接返回true 
    if (row == board.length) 
        return true; 
    //如果当前行的最后一列也遍历完了，就从下一行的第一列开始。这里的遍历    //顺序是从第1行的第1列一直到最后一列，然后第二行的第一列一直到最后 
    //一列，然后第三行的……    if (col == board.length) 
        return backTrace(board, row + 1, 0); 
    //如果当前位置已经有数字了，就不能再填了，直接到这一行的下一列    if (board[row][col] != '.') 
        return backTrace(board, row, col + 1); 
    //如果上面条件都不满足，我们就从1到9中选择一个合适的数字填入到数独中 
    for (char i = '1'; i <= '9'; i++) { 
        //判断当前位置[row，col]是否可以放数字i，如果不能放再判断下        //一个能不能放，直到找到能放的为止，如果从1-9都不能放，就会下面 
        //直接return false 
        if (!isValid(board, row, col, i)) 
            continue;        //如果能放数字i，就把数字i放进去        board[row][col] = i;        //如果成功就直接返回，不需要再尝试了        if (backTrace(board, row, col)) 
            return true; 
        //否则就撤销重新选择        board[row][col] = '.'; 
    }    //如果当前位置[row，col]不能放任何数字，直接返回false 
    return false; 
}//验证当前位置[row，col]是否可以存放字符cprivate static boolean isValid(char[][] board, int row, int col, char c) { 
    for (int i = 0; i < 9; i++) { 
        if (board[i][col] != '.' && board[i][col] == c) 
            return false; 
        if (board[row][i] != '.' && board[row][i] == c) 
            return false; 
        if (board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] != '.' && 
                board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == c) 
            return false; 
    }    return true; 
}

总结

回溯算法要和递归结合起来就很好理解了，递归分为两部分，第一部分是先往下传递，第二部分到达终止条件的时候然后再反弹往回走，我们来看一下阶乘的递归

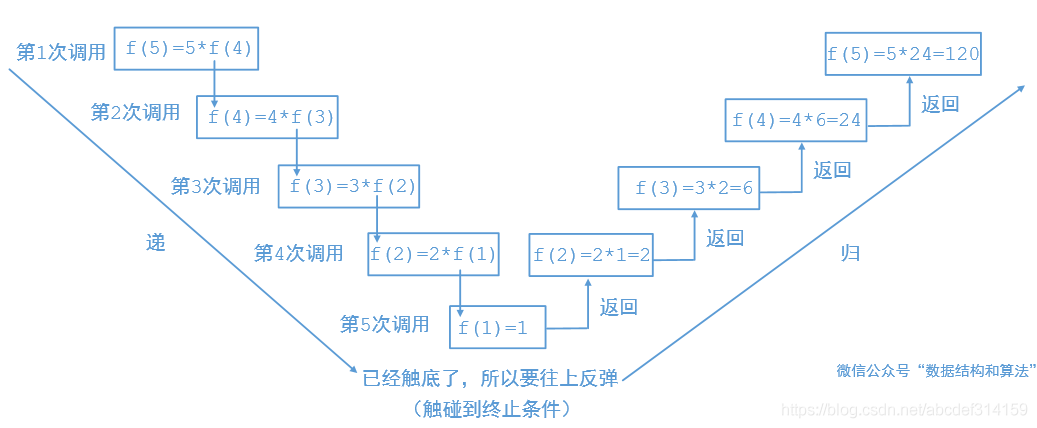
其实回溯算法就是在往下传递的时候把某个值给改变，然后往回反弹的时候再把原来的值复原即可。比如八皇后的时候我们先假设一个位置可以放皇后，如果走不通就把当前位置给撤销，放其他的位置。如果是组合之类的问题，往下传递的时候我们把当前值加入到list中，然后往回反弹的时候在把它从list中给移除掉即可。