你也是数独爱好者吗?
Aakash Jhawar和许多人一样,乐于挑战新的难题。上学的时候,他每天早上都要玩数独。长大后,随着科技的进步,我们可以让计算机来帮我们解数独了!只需要点击数独的图片,它就会为你填满全部九宫格。
叮~ 这里有一份数独解析教程,等待你查收~ 喜欢收藏硬核干货的小伙伴看过来~
我们都知道,数独由9×9的格子组成,每行、列、宫各自都要填上1-9的数字,要做到每行、列、宫里的数字都不重复。
可以将解析数独的整个过程分成3步:
第一步:从图像中提取数独
第二步:提取图像中出现的每个数字
第三步:用算法计算数独的解
第一步:从图像中提取数独
首先需要进行图像处理。
1、对图像进行预处理
首先,我们应用高斯模糊的内核大小(高度,宽度)为9的图像。注意,内核大小必须是正的和奇数的,并且内核必须是平方的。然后使用11个最近邻像素自适应阈值。
- proc = cv2.GaussianBlur(img.copy(),(9,9),0)
- proc = cv2.adaptiveThreshold(proc,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,cv2.THRESH_BINARY,11,2)
为了使网格线具有非零像素值,我们颠倒颜色。此外,把图像放大,以增加网格线的大小。
- proc = cv2.bitwise_not(proc,proc)
- kernel = np.array([[0。,1.,0.],[1.,1.,1.],[0.,1.,0.]] ,np.uint8)
- proc = cv2.dilate(proc,kernel)
阈值化后的数独图像
2、找出最大多边形的角
下一步是寻找图像中最大轮廓的4个角。所以需要找到所有的轮廓线,按面积降序排序,然后选择面积最大的那个。
- _, contours, h = cv2.findContours(img.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
- contours = sorted(contours, key=cv2.contourArea, reverse=True)
- polygon = contours[0]
使用的操作符。带有max和min的itemgetter允许我们获得该点的索引。每个点都是有1个坐标的数组,然后[0]和[1]分别用于获取x和y。
右下角点具有最大的(x + y)值;左上角有点最小(x + y)值;左下角则具有最小的(x - y)值;右上角则具有最大的(x - y)值。
- bottom_right, _ = max(enumerate([pt[0][0] + pt[0][1] for pt in
- polygon]), key=operator.itemgetter(1))
- top_left, _ = min(enumerate([pt[0][0] + pt[0][1] for pt in
- polygon]), key=operator.itemgetter(1))
- bottom_left, _ = min(enumerate([pt[0][0] - pt[0][1] for pt in
- polygon]), key=operator.itemgetter(1))
- top_right, _ = max(enumerate([pt[0][0] - pt[0][1] for pt in
- polygon]), key=operator.itemgetter(1))
现在我们有了4个点的坐标,然后需要使用索引返回4个点的数组。每个点都在自己的一个坐标数组中。
- [polygon[top_left][0], polygon[top_right][0], polygon[bottom_right][0], polygon[bottom_left][0]]
最大多边形的四个角
3、裁剪和变形图像
有了数独的4个坐标后,我们需要剪裁和弯曲一个矩形部分,从一个图像变成一个类似大小的正方形。由左上、右上、右下和左下点描述的矩形。
注意:将数据类型显式设置为float32或‘getPerspectiveTransform’会引发错误。
- top_left, top_right, bottom_right, bottom_left = crop_rect[0], crop_rect[1], crop_rect[2], crop_rect[3]
- src = np.array([top_left, top_right, bottom_right, bottom_left], dtype= float32 )
- side = max([ distance_between(bottom_right, top_right),
- distance_between(top_left, bottom_left),
- distance_between(bottom_right, bottom_left),
- distance_between(top_left, top_right) ])
用计算长度的边来描述一个正方形,这是要转向的新视角。然后要做的是通过比较之前和之后的4个点来得到用于倾斜图像的变换矩阵。最后,再对原始图像进行变换。
- dst = np.array([[0, 0], [side - 1, 0], [side - 1, side - 1], [0, side - 1]], dtype= float32 )
- m = cv2.getPerspectiveTransform(src, dst)
- cv2.warpPerspective(img, m, (int(side), int(side)))
裁剪和变形后的数独图像
4、从正方形图像中推断网格
从正方形图像推断出81个单元格。我们在这里交换 j 和 i ,这样矩形就被存储在从左到右读取的列表中,而不是自上而下。
- squares = []
- side = img.shape[:1]
- sideside = side[0] / 9
- for j in range(9):
- for i in range(9):
- p1 = (i * side, j * side) #Top left corner of a box
- p2 = ((i + 1) * side, (j + 1) * side) #Bottom right corner
- squares.append((p1, p2)) return squares
5、得到每一位数字
下一步是从其单元格中提取数字并构建一个数组。
- digits = []
- img = pre_process_image(img.copy(), skip_dilate=True)
- for square in squares:
- digits.append(extract_digit(img, square, size))
extract_digit 是从一个数独方块中提取一个数字(如果有的话)的函数。它从整个方框中得到数字框,使用填充特征查找来获得框中间的最大特征,以期在边缘找到一个属于该数字的像素,用于定义中间的区域。接下来,需要缩放并填充数字,让适合用于机器学习的数字大小的平方。同时,我们必须忽略任何小的边框。
- def extract_digit(img, rect, size):
- digit = cut_from_rect(img, rect)
- h, w = digit.shape[:2]
- margin = int(np.mean([h, w]) / 2.5)
- _, bbox, seed = find_largest_feature(digit, [margin, margin], [w
- - margin, h - margin])
- digit = cut_from_rect(digit, bbox)
- w = bbox[1][0] - bbox[0][0]
- h = bbox[1][1] - bbox[0][1]
- if w > 0 and h > 0 and (w * h) > 100 and len(digit) > 0:
- return scale_and_centre(digit, size, 4)
- else:
- return np.zeros((size, size), np.uint8)
最后的数独的形象
现在,我们有了最终的数独预处理图像,下一个任务是提取图像中的每一位数字,并将其存储在一个矩阵中,然后通过某种算法计算出数独的解。
第二步:提取图像中出现的每个数字
对于数字识别,我们将在MNIST数据集上训练神经网络,该数据集包含60000张0到9的数字图像。从导入所有库开始。
- import numpy
- import cv2from keras.datasets
- import mnistfrom keras.models
- import Sequentialfrom keras.layers
- import Densefrom keras.layers
- import Dropoutfrom keras.layers
- import Flattenfrom keras.layers.convolutional
- import Conv2Dfrom keras.layers.convolutional
- import MaxPooling2Dfrom keras.utils
- import np_utilsfrom keras
- import backend as K
- import matplotlib.pyplot as plt
需要修复随机种子以确保可重复性。
- K.set_image_dim_ordering( th )
- seed = 7numpy.random.seed(seed)
- (X_train, y_train), (X_test, y_test) = mnist.load_data()
然后将图像重塑为样本*像素*宽度*高度,并输入从0-255规范化为0-1。在此之后,对输出进行热编码。
- X_trainX_train = X_train.reshape(X_train.shape[0], 1, 28,
- 28).astype( float32 )
- X_testX_test = X_test.reshape(X_test.shape[0], 1, 28,
- 28).astype( float32 )
- X_trainX_train = X_train / 255
- X_testX_test = X_test / 255
- y_train = np_utils.to_categorical(y_train)
- y_test = np_utils.to_categorical(y_test)
- num_classes = y_test.shape[1]
接下来,我们将创建一个模型来预测手写数字。
- model = Sequential()
- model.add(Conv2D(32, (5, 5), input_shape=(1, 28, 28),
- activation= relu ))
- model.add(MaxPooling2D(pool_size=(2, 2)))model.add(Conv2D(16, (3,
- 3), activation= relu ))
- model.add(MaxPooling2D(pool_size=(2, 2)))
- model.add(Dropout(0.2))
- model.add(Flatten())
- model.add(Dense(128, activation= relu ))
- model.add(Dense(64, activation= relu ))
- model.add(Dense(num_classes, activation= softmax ))
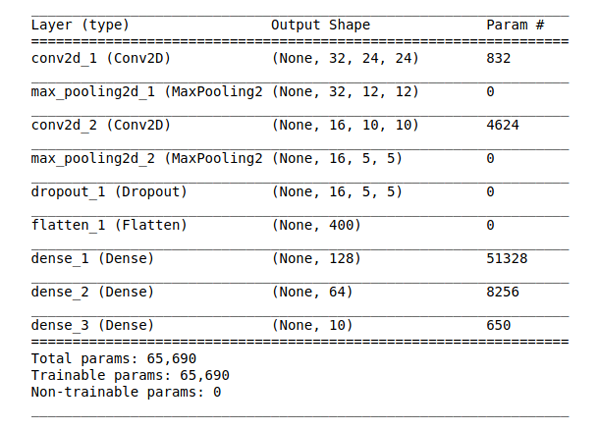
模型总结
在创建模型之后,需要进行编译,使其适合数据集并对其进行评估。
- model.compile(loss= categorical_crossentropy , optimizer= adam ,
- metrics=[ accuracy ])
- model.fit(X_train, y_train, validation_data=(X_test, y_test),
- epochs=10, batch_size=200)
- scores = model.evaluate(X_test, y_test, verbose=0)
- print("Large CNN Error: %.2f%%" % (100-scores[1]*100))
现在,可以测试上面创建的模型了。
- test_images = X_test[1:5]
- test_imagestest_images = test_images.reshape(test_images.shape[0], 28, 28)
- print ("Test images shape: {}".format(test_images.shape))
- for i, test_image in enumerate(test_images, start=1):
- org_image = test_image
- test_imagetest_image = test_image.reshape(1,1,28,28)
- prediction = model.predict_classes(test_image, verbose=0)
- print ("Predicted digit: {}".format(prediction[0]))
- plt.subplot(220+i)
- plt.axis( off )
- plt.title("Predicted digit: {}".format(prediction[0]))
- plt.imshow(org_image, cmap=plt.get_cmap( gray ))
- plt.show()
手写体数字分类模型的预测数字
神经网络的精度为98.314%!最后,保存序列模型,这样就不必在需要使用它的时候反复训练了。
- # serialize model to JSON
- modelmodel_json = model.to_json()
- with open("model.json", "w") as json_file:
- json_file.write(model_json)
- # serialize weights to HDF5
- model.save_weights("model.h5")
- print("Saved model to disk")
更多关于手写数字识别的信息:
https://github.com/aakashjhawar/Handwritten-Digit-Recognition
下一步是加载预先训练好的模型。
- json_file = open( model.json , r )
- loaded_model_json = json_file.read()
- json_file.close()
- loaded_model = model_from_json(loaded_model_json)
- loaded_model.load_weights("model.h5")
调整图像大小,并将图像分割成9x9的小图像。每个小图像的数字都是从1-9。
- sudoku = cv2.resize(sudoku, (450,450))
- grid = np.zeros([9,9])
- for i in range(9):
- for j in range(9):
- image = sudoku[i*50:(i+1)*50,j*50:(j+1)*50]
- if image.sum() > 25000:
- grid[i][j] = identify_number(image)
- else:
- grid[i][j] = 0
- gridgrid = grid.astype(int)
identify_number 函数拍摄数字图像并预测图像中的数字。
- def identify_number(image):
- image_resize = cv2.resize(image, (28,28)) # For plt.imshow
- image_resizeimage_resize_2 = image_resize.reshape(1,1,28,28) # For input to model.predict_classes
- # cv2.imshow( number , image_test_1)
- loaded_modelloaded_model_pred = loaded_model.predict_classes(image_resize_2
- , verbose = 0)
- return loaded_model_pred[0]
完成以上步骤后,数独网格看起来是这样的:
提取的数独
第三步:用回溯算法计算数独的解
我们将使用回溯算法来计算数独的解。
在网格中搜索仍未分配的条目。如果找到引用参数行,col 将被设置为未分配的位置,而 true 将被返回。如果没有未分配的条目保留,则返回false。“l” 是 solve_sudoku 函数传递的列表变量,用于跟踪行和列的递增。
- def find_empty_location(arr,l):
- for row in range(9):
- for col in range(9):
- if(arr[row][col]==0):
- l[0]=row
- l[1]=col
- return True
- return False
返回一个boolean,指示指定行的任何赋值项是否与给定数字匹配。
- def used_in_row(arr,row,num):
- for i in range(9):
- if(arr[row][i] == num):
- return True
- return False
返回一个boolean,指示指定列中的任何赋值项是否与给定数字匹配。
- def used_in_col(arr,col,num):
- for i in range(9):
- if(arr[i][col] == num):
- return True
- return False
返回一个boolean,指示指定的3x3框内的任何赋值项是否与给定的数字匹配。
- def used_in_box(arr,row,col,num):
- for i in range(3):
- for j in range(3):
- if(arr[i+row][j+col] == num):
- return True
- return False
检查将num分配给给定的(row, col)是否合法。检查“ num”是否尚未放置在当前行,当前列和当前3x3框中。
- def check_location_is_safe(arr,row,col,num):
- return not used_in_row(arr,row,num) and
- not used_in_col(arr,col,num) and
- not used_in_box(arr,row - row%3,col - col%3,num)
采用部分填入的网格,并尝试为所有未分配的位置分配值,以满足数独解决方案的要求(跨行、列和框的非重复)。“l” 是一个列表变量,在 find_empty_location 函数中保存行和列的记录。将我们从上面的函数中得到的行和列赋值给列表值。
- def solve_sudoku(arr):
- l=[0,0]
- if(not find_empty_location(arr,l)):
- return True
- row=l[0]
- col=l[1]
- for num in range(1,10):
- if(check_location_is_safe(arr,row,col,num)):
- arr[row][col]=num
- if(solve_sudoku(arr)):
- return True
- # failure, unmake & try again
- arr[row][col] = 0
- return False
最后一件事是print the grid。
- def print_grid(arr):
- for i in range(9):
- for j in range(9):
- print (arr[i][j])
- print ( )
最后,把所有的函数整合在主函数中。
- def sudoku_solver(grid):
- if(solve_sudoku(grid)):
- print( --- )
- else:
- print ("No solution exists")
- gridgrid = grid.astype(int)
- return grid
这个函数的输出将是最终解出的数独。
最终的解决方案
当然,这个解决方案绝不是万无一失的,处理图像时仍然会出现一些问题,要么无法解析,要么解析错误导致无法处理。不过,我们的目标是探索新技术,从这个角度来看,这个项目还是有价值的。