前言
动态规划的算法题经常出现在大厂的面试中,它是非常适合考查候选人的一类题型,因为它难度适中,需要一定的技巧,而且根据习题可以有一定的变化,所以如果想去大厂,建议大家好好刷一下此类题目,接下来我会写一些动态规划的相关题解,希望能对大家理解此类习题有所帮助。
今天我们来看一道腾讯面试题,题目如下:
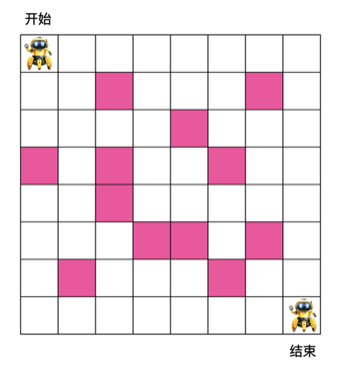
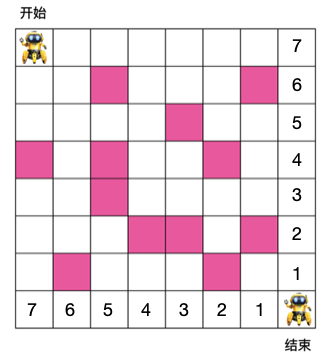
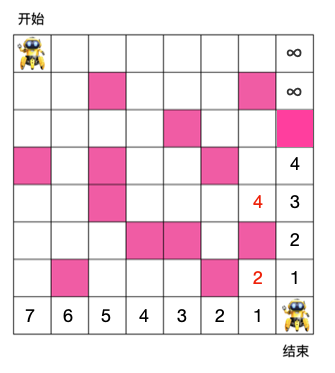
有如下 8 x 8 格子,机器人需要从入口走到出口,每次只能朝右或朝下走,粉色格子为障碍物,机器人不能穿过,问机器人从入口走到出口最少需要的步数是多少?
题解分析
这道题其实我们之前在前文解析过类似的题目,只不过当时求的是从入口到出口最多共有多少种走法,而本题稍微变化了一下,求的是最少需要的步数。整体思路其实是一样的,大家可以先看看前文,思考一下,然后再看看我的题解。
首先最容易想到的当然是暴力解法,对于机器人来说,每一步都可以向下或向右走
所以我们可以用暴力算法求出所有路径所需求步数,然后求其最小步数,伪代码如下
- paths(start, end) = 1+min(paths(start下方格子, end), paths(start右边格子, end))
时间复杂度是多少?对于机器人所处的每一个格子来说,下一步可以走两步(向右或向下),共有 N 个格子,所以共有 O(2^n) 步可走,指数级别!暴力解法显然有很大的问题。
这道题其实考察的是用动态规划的思想来求解。
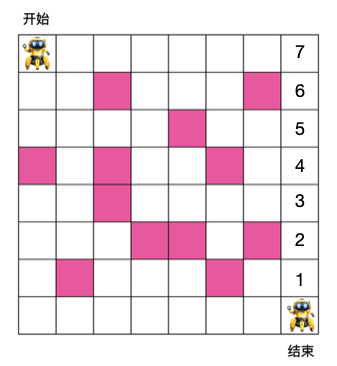
动态规划主要解题思路是用自底向上的思想来求解,求入口到出口的最短路径叫自顶向上,而求出口到入口的最短路径即为自底向上。怎么求,我们先看下出口的上一个位置。
对这个位置来说,它往出口走只需要一步,所以我们在它的位置上填1,同理,它的上一个位置必须经由此位置走到出口,所以它的上一个位置应该填 2,依此类推,我们可以在右边填上这些格子走到出口的步数
同理可得底部的格子到出口的位置,如下:
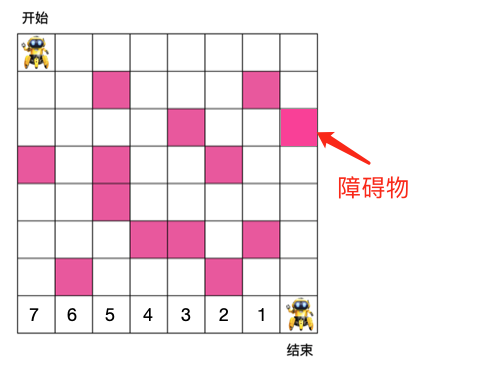
可能有人会说了,如果右边和底边有个格子有障碍物咋办,如下
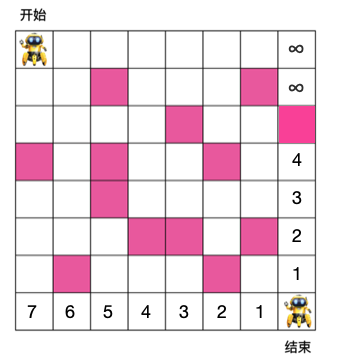
对于这种情况,由于障碍物上面的格子不可能通向出口,所以障碍物上面的格子应该填无穷大(另外,显而易见,所有障碍物本身所在格子应该填无穷大),如下
以上最右列和最底边格子所填数字即为动态规划的 base case,求完了 base case,还要得出动态规划的「状态转移方程」,得出状态转移方程后,动态规划求解基本上就大功告成了,一起来看下怎么求解。
现在我们再从右到左,从下到上依次遍历每个格子,求出每个格子到出口的最小步数,我们知道每个格子的下一步只能向右或向下,所以每个格子到出口的最小步数可按如下公式求解
当前格子到出口的最小步数 = 1 + min(右格子到出口最小步数,下方格子到出口的最小步数)
此公式即为状态转移方程
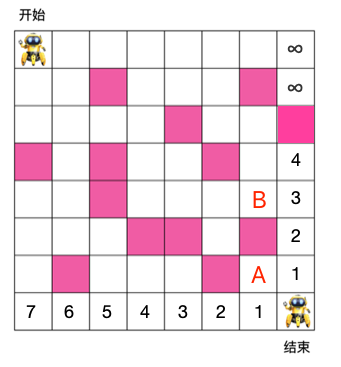
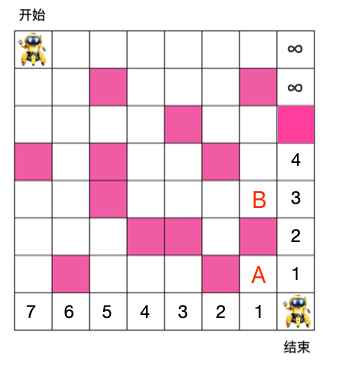
举个例子,以下方的 A,B 两个格子为例
对于 A 格子来说,它的右格子,下方格子到出口的最小步数是 1,所以其到出口的最小步数为 1+min(1,1) = 2。
对于 B 来说,它右格子到出口的最小步数为 3,其下格子是障碍物,到出口的步数为无穷大,所以 B 到出口的最小步数为 1 + min(∞, 3) = 4。如下
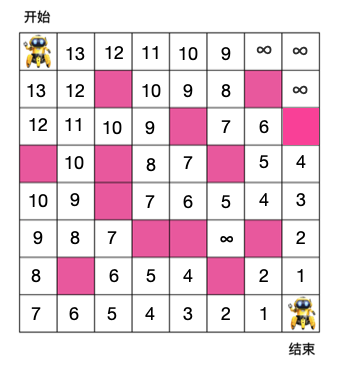
依此类推,我们可以得出每个格子到出口的最小步数,如下所示:
填满之后到了入口位置,显然入口到出口的最少步数应该是 1 + min(13,13) = 14 步。以下是代码,注释写得很清楚了,相信大家应该能看懂。
- public class Solution {
- /**
- * 初始化格子,假设为 8 x 8, -1 代表格子为障碍物
- */
- private static final int GRIDS[][] = {
- {0,0,0,0,0,0,0,0},
- {0,0,-1,0,0,0,-1,0},
- {0,0,0,0,-1,0,0,0},
- {-1,0,-1,0,0,-1,0,0},
- {0,0,-1,0,0,0,0,0},
- {0,0,0,-1,-1,0,-1,0},
- {0,-1,0,0,0,-1,0,0},
- {0,0,0,0,0,0,0,0}
- };
- static private int getMinStep() {
- /**
- * 格子为 8 x 8
- */
- int N = 8;
- // 如果格子为障碍物,则此格子到出口的距离标记为无究大(这里用100000表示),代表此格子到出口不通
- Integer infinity = 100000;
- /**
- * 初始化最右边的格子,从最后一列的倒数第二行开始(因为最后一个格子为出口)
- */
- for (int row = N-2; row >= 0; row--) {
- // 如果当前格子的下一个格子不是障碍物,则当前格子到出口的最小步数为 1 + 下个格子到出口的步数
- if (GRIDS[row+1][N-1] != -1) {
- GRIDS[row][N-1] = 1 + GRIDS[row+1][N-1];
- } else {
- // 如果下一个格子是障碍物,则此格子到出口的步数设置为无穷大(代表此路不通),这里用正整数的最大值表示
- GRIDS[row][N-1] = infinity;
- }
- }
- /**
- * 初始化最底部的格子,从最后一行的倒数第二列开始(因为最后一个格子为出口)
- */
- for (int column = N-2; column >= 0; column--) {
- // 如果当前格子右边的格子不是障碍物,则当前格子到出口的最小步数为 1 + 右格子到出口的步数
- if (GRIDS[N-1][column+1] != -1) {
- GRIDS[N-1][column] = 1 + GRIDS[N-1][column+1];
- } else {
- // 如果是障碍物,则到出口的步数为无穷大,这里用正整数的最大值表示
- GRIDS[N-1][column] = infinity;
- }
- }
- /**
- * 从右到左,从下到上填满每个格子的值,由于最右和最底部的格子都初始化了,
- * 所以从倒数第二行,倒数第二列开始遍历
- */
- for (int i = N - 2; i >= 0; i--) {
- for (int j = N - 2; j >= 0; j--) {
- // 说明是障碍物,所在格子到出口步数显然为无穷大(代表此路不通)
- if (GRIDS[i][j] == -1) {
- GRIDS[i][j] = infinity;
- continue;
- }
- /**
- * 当前格子到出口的最小步数为1+(右边的格子到出口的步数与下格子到出口步数之和的最小值)
- */
- GRIDS[i][j] = 1 + Math.min(GRIDS[i+1][j], GRIDS[i][j+1]);
- }
- }
- /**
- * 遍历完之后起点格子对应的值即为最终所求的解
- */
- return GRIDS[0][0];
- }
- public static void main(String[] args) {
- int result = Solution.getMinStep();
- System.out.println("result = " + result);
- }
- }
理清了思路,剩下用代码实现就相对简单了,接下来我们分析下时间复杂度和空间复杂度。
时间复杂度中间有两层循环,所以显然为 O(N^2),空间复杂度呢,我们并没有分配额外的空间来存储数据,而是复用了代表迷宫的格子数组 GRIDS,所以空间复杂度为 O(1)。有人可能会问了,为啥可以直接用 GRIDS 来计算格子到出口的步数,这样不就把格子的信息(如是否是障碍物)给覆盖了吗。这里就要了解一下动态规划的无后效性了,啥叫无后效性。
以上文所举例子为例,对于图中的 A,B 格子来说,由状态转移方程
- 当前格子到出口的最小步数 = 1 + min(右格子到出口最小步数,下方格子到出口的最小步数)
可知,计算它到出口的最短步数只与它的右格子与下方格子到出口的最小步数有关(此时右格子与下方格子的步数已经计算出来)也就是说对于 A,B 格子来说,它只关心它的右格子与下方格子中的步数,至于这两个格子的步数是如何算出来的,它们不关心,这就叫无后效性。
所以我们可以从右到左,从下到上依次遍历每个格子的步数,将其填入 GRIDS 中,这样虽然 GRIDS 中的格子信息被覆盖了,但对计算被遍历到的格子到出口的步数没有影响。巧妙使用无后效性在很多场景下可以有效压缩空间,降低空间复杂度。
本文转载自微信公众号「码海」,可以通过以下二维码关注。转载本文请联系码海公众号。