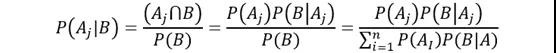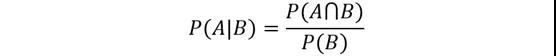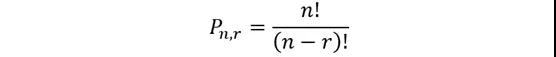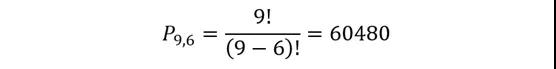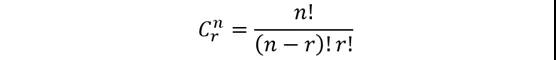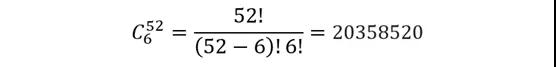从某些角度上来讲,如今的数据科学家基本上等于现代统计学家。在数据科学面试中,我们也少不了要面对统计学相关的知识。
以下是数据科学相关面试中最频繁出现的三种统计学问题,它们是许多数据科学应用程序的基本构建模块。还有一些非常重要的统计学概念本文没有提到,比如中心极限定理,但是在提及概率分布时它仍然是不可或缺。
接下来就开始吧!
1. 贝叶斯定理/条件概率
你需要理解贝叶斯定理和条件概率,因为最流行的机器学习算法之一——朴素贝叶斯算法就是建立在这两个概念上的。此外,如果你研究的是在线机器学习,你很可能会需要使用贝叶斯算法。
贝叶斯定理/条件概率
问题示例:你即将登上飞往西雅图的飞机,想知道是否应该带把伞。你随机打电话给3个住在那里的朋友,分别问他们西雅图是否在下雨。每一个朋友都有2/3的机会告诉你真相,1/3的机会说谎来搅乱你。结果3个朋友都告诉你“是的,西雅图在下雨”。那么西雅图下雨的概率是多少?
贝叶斯定理
条件概率
答:可以看出这个问题与贝叶斯理论有关,因为最后一个陈述基本遵循了这个结构,即“如果B为真,A为真的概率是多少?”因此,我们需要知道西雅图某一天下雨的概率。假设这个概率是25%。
- P(A) =下雨的概率= 25%
- P(B) =三个朋友都说下雨的概率
- P(A |B)是“假设朋友说下雨,那么真实下雨”的概率
- P(B|A) 是“假设真的在下雨,那么3个朋友都说在下雨”的概率= (2/3)3 = 8/27
步骤一:求解P(B)
- P(A|B) = P(B|A) * P(A) / P(B),可以写作——P(B) = P(B|A) * P(A) + P(B|非 A) * P(非 A)
- P(B) = (2/3)3 * 0.25 + (1/3)3 * 0.75 = 0.25*8/27 + 0.75*1/27
步骤二:求解P(A|B)
- P(A|B) = 0.25 * (8/27) / ( 0.25*8/27 + 0.75*1/27)
- P(A|B) = 8 / (8 + 3) = 8/11
因此,如果三个朋友都说下雨了,那么下雨的概率是8/11。
2. 计算应用
如果你正在从事网络安全、模式分析、运筹学等工作,那么组合和排列是极其重要的。让我们再回顾一下它们的概念:
排列
定义:n个元素的排列是指将这n个元素按照一定的顺序排列。排列n个元素有n的阶乘种方法。注意,顺序很重要!
一次取r的n个事物的排列数被定义为可以从n个不同元素中提取的r元组的数目,它等于以下等式:
例题:一个6位数的车牌有多少种排列方式?
答案
组合
定义:在顺序无关紧要的n个对象中选择r的方法数。
一次取r的n个事物的组合数定义为一个有n个元素的集合中有r个元素的子集的个数,等于:
例题:从52张牌中抽出6张牌的方法有多少种?
答案
这些都是非常简单的问题,而你真实遇到的可能会比这复杂得多,但万变不离其宗,所以你要充分理解上面的例子。
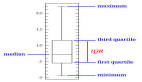
3. 概率分布/置信区间
我们很容易在概率分布中感到迷茫,因为概率分布形式实在太多了。如果必须选择五个主要的分布来介绍,它们会是:
- 正态分布
- 泊松分布
- 二项分布
- 指数分布
- ·均匀分布
问题:苏格兰去年的凶杀率从前年的115人下降到99人。这些报道的变化真的值得注意吗?
答:这是一个泊松分布问题,平均值=λ=方差,这也意味着标准差=平均值的平方根。
- 95%置信区间意味着z值为1.96。
- 一个标准差=√115 = 10.724
因此,置信区间=115+/-21.45=[93.55,136.45]。由于99在这个置信区间内,我们可以假设这种变化不是很值得注意。
文中给出的例子看起来都不难,但生动地表达了这些包罗万象的概念的核心内容,希望能帮助你对这三个重要概念有基本理解。
本文转载自微信公众号「读芯术」,可以通过以下二维码关注。转载本文请联系读芯术公众号。