链表是一种常见的数据结构,链表是由一连串的结点组成,这个节点就是链结点,每个链结点都由数据域和指针域两部分组成。
使用链表结构可以克服数组结构需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
链表比较好的一种理解是:将链表看成一个火车,每个车厢之间都是相互连接的,只要找到火车头,就可以找到具体的车身。链表也是,我们只关心它的头。
一 单向链表
1.1 单向链表原理图
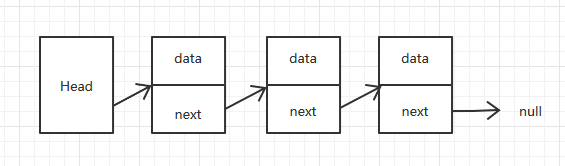
单向链表的一个链结点包含数据域和下一个链结点的指针。头结点也包含数据域和指针域,但是一般为了方便查找,头节点不写数据,最后一个结点的指针指向空。
1.2 实现单向链表的存储等操作
创建一个链结点的实体类
- public class Node {
- // 数据域
- public long data;
- // 指针域
- public Node next;
- public Node(long value){
- this.data = value;
- }
- }
1.2.1 插入一个节点
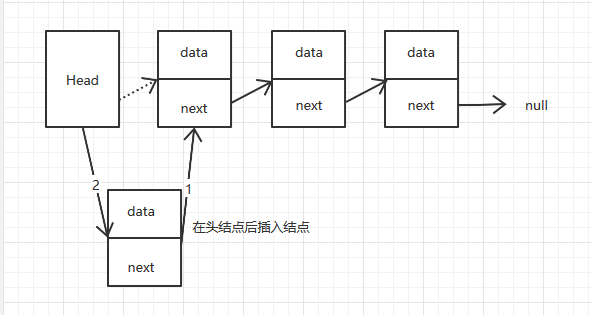
在头节点后插入一个结点,第一步需要将新插入的结点指向头结点指向的结点,第二步将头结点指向新插入的结点。插入结点只需要改变一个引用,所以复杂度为O(1)。
- public class LinkList {
- private Node head;
- /**
- * 在头节点之后插入一个节点
- */
- public void insertFirst(long value){
- Node node = new Node(value);
- node.next = head;
- head = node;
- }
- }
1.2.2 头结点后删除一个结点
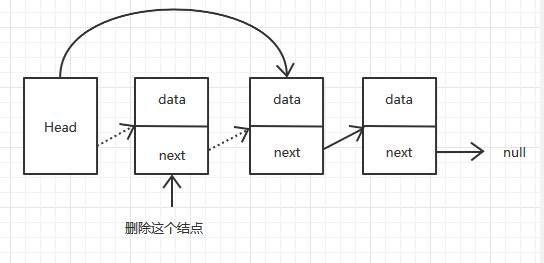
在头结点后删除一个结点,就是让头结点指向这个结点的下一个结点。复杂度也是O(1)。
- public Node deleteFirst(){
- Node tmp = head;
- head = tmp.next;
- return tmp;
- }
1.2.3 根据数据域查找结点
查找需要比对每个结点的数据,理论上查找一个结点平均需要N/2次,所以复杂度为O(N)。
- public Node find(long value){
- Node current = head;
- while (current.data != value){
- if(current.next == null){
- return null;
- }
- current = current.next;
- }
- return current;
- }
1.2.4 根据数据与删除结点
查找需要比对每个结点的数据,理论上删除一个结点平均需要N/2次,所以复杂度为O(N)。
- public Node delete(int value){
- Node current = head;
- // 当前结点的前一个结点
- Node pre = head;
- while (current.data != value){
- if(current.next == null){
- return null;
- }
- pre = current;
- current = current.next;
- }
- if(current == head){
- head = head.next;
- }else{
- pre.next = current.next;
- }
- return current;
- }
二 双端链表
2.1 双端链表原理图
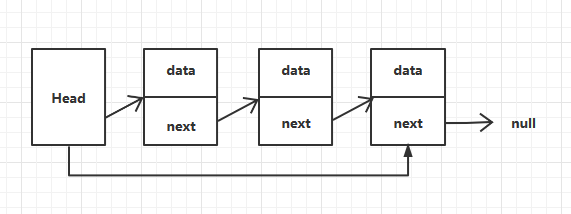
双端链表是在单向链表的基础上,头结点增加了一个尾结点的引用。
2.2 实现双端链表的存储等操作
2.2.1 从头部插入结点
如果链表为空,则设置尾结点就是新添加的结点。复杂度为O(1)。
- public class FirstLastLinkList {
- private Node first;
- private Node last;
- /**
- * 在头结点之后插入一个节点
- */
- public void insertFirst(long value){
- Node node = new Node(value);
- if(first == null){
- last = node;
- }
- node.next = first;
- first = node;
- }
- }
2.2.2 从尾部插入结点
如果链表为空,则设置头结点为新添加的结点,否则设置尾结点的后一个结点为新添加的结点。复杂度为O(1)。
- public void insertLast(long value){
- Node node = new Node(value);
- if(first == null){
- first = node;
- }else{
- last.next = node;
- }
- last = node;
- }
2.2.3 从头部进行删除
判断头结点是否有下一个结点,如果没有则设置尾结点为null,复杂度为O(1)。
- public Node deleteFirst(){
- Node tmp = first;
- if(first.next == null){
- last = null;
- }
- first = tmp.next;
- return tmp;
- }
三 双向链表
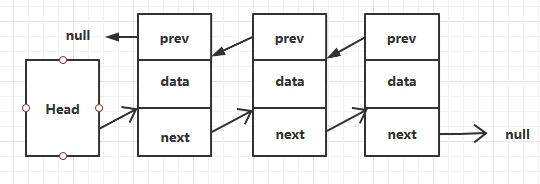
3.1 双向链表原理图
每个结点除了保存对后一个结点的引用外,还保存着对前一个结点的引用。
3.2 实现双向链表的存储等操作链结点实体类
- public class Node {
- // 数据域
- public long data;
- // 后一个结点指针域
- public Node next;
- // 前一个结点指针域
- public Node prev;
- public Node(long value){
- this.data = value;
- }
- }
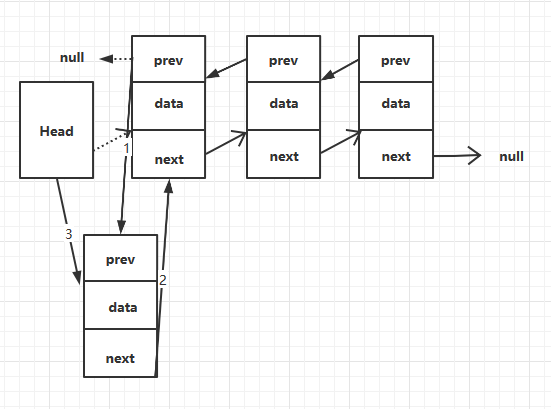
3.2.1 从头部插入结点
如果链表为空,则设置尾结点为新添加的结点,如果不为空,还需要设置头结点的前一个结点为新添加的结点。插入结点只需要改变两个结点的引用,所以复杂度为O(1)。
- public class DoubleLinkList {
- private Node first;
- private Node last;
- /**
- * 在头结点之后插入一个节点
- */
- public void insertFirst(long value){
- Node node = new Node(value);
- if(first == null){
- last = node;
- } else{
- first.prev = node;
- }
- node.next = first;
- first = node;
- }
- }
3.2.2 从尾部插入结点
如果链表为空,则设置头结点为新添加的结点,否则设置尾结点的后一个结点为新添加的结点。同时设置新添加的结点的前一个结点为尾结点。插入结点只需要改变1个结点的引用,所以复杂度为O(1)。
- public void insertLast(long value){
- Node node = new Node(value);
- if(first == null){
- first = node;
- }else{
- last.next = node;
- node.prev = last;
- }
- last = node;
- }
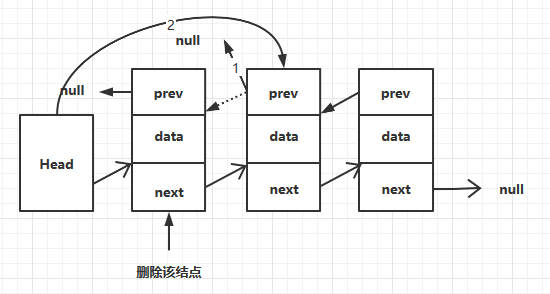
3.2.3 从头部删除结点
判断头结点是否有下一个结点,如果没有则设置尾结点为null,否则设置头结点的下一个结点的prev为null。复杂度也为O(1)。
- public Node deleteFirst(){
- Node tmp = first;
- if(first.next == null){
- last = null;
- }else{
- first.next.prev = null;
- }
- first = tmp.next;
- return tmp;
- }
3.2.4 从尾部删除结点
如果头结点后没有其他结点,则设置头结点为null,否则设置尾结点的前一个结点的next为null,设置尾结点为前一个结点。复杂度为O(1)。
- public Node deleteLast(){
- Node tmp = last;
- if(first.next == null){
- first = null;
- }else{
- last.prev.next = null;
- }
- last = last.prev;
- return last;
- }
四 总结
链表包含一个头结点和多个结点,头结点包含一个引用,这个引用通常叫做first,它指向链表的第一个链结点。结点的next为null,则意味着这个结点是尾结点。与数组相比,链表更适合做插入、删除操作,而查找操作的复杂度更高。还有一个优势就是链表不需要初始化内存大小,不会造成内存溢出(数组中插入元素个数超过数组长度)或内存浪费(声明的数组长度比实际放的元素长)。
本文转载自微信公众号「Java旅途」,可以通过以下二维码关注。转载本文请联系Java旅途公众号。