JavaScript实现栈结构（Stack）-javascript全栈开发

[[337051]]

本文转载自微信公众号「泰斗贤若如」，作者AhuntSun 。转载本文请联系泰斗贤若如公众号。

一、前言

1.1.什么是数据结构?

数据结构就是在计算机中，存储和组织数据的方式。

例如：图书管理，怎样摆放图书才能既能放很多书，也方便取?

主要需要考虑两个问题：

操作一：新书怎么插入?
操作二：怎么找到某本指定的书?

「常见的数据结构：」

「数组」(Aarray)
「栈」(Stack)
「链表」(Linked List)
「图」(Graph)
「散列表」(Hash)
「队列」(Queue)
「树」(Tree)
「堆」(Heap)

「注意」：数据结构与算法与语言无关，常见的编程语言都有「直接或间接」的使用上述常见的数据结构。

1.2.什么是算法?

算法(Algorithm)的定义

一个有限指令集，每条指令的描述不依赖于语言;
接收一些输入(有些情况下不需要输入);
产生输入;
一定在有限步骤之后终止;

算法通俗理解：解决问题的办法/步骤逻辑。数据结构的实现，离不开算法。

二、栈结构(Stack)

2.1.简介

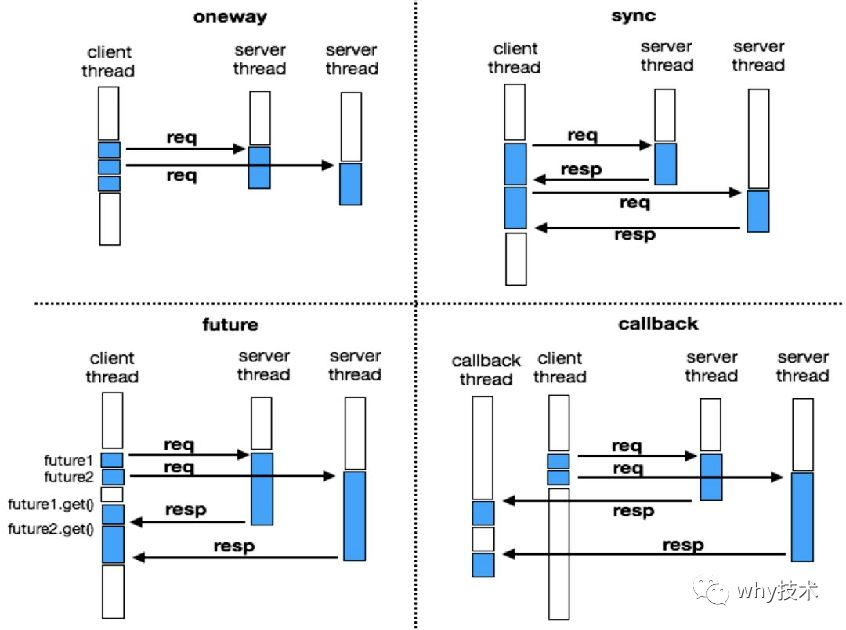
数组是一个线性结构，并且可以在数组的「任意位置」插入和删除元素。而「栈和队列」就是比较常见的「受限的线性结构」。如下图所示：

image-20200226131817102

栈的特点为「先进后出，后进先出」(LIFO：last in first out)。

「程序中的栈结构：」

「函数调用栈」：A(B(C(D())))：即A函数中调用B，B调用C，C调用D;在A执行的过程中会将A压入栈，随后B执行时B也被压入栈，函数C和D执行时也会被压入栈。所以当前栈的顺序为：A->B->C->D(栈顶);函数D执行完之后，会弹出栈被释放，弹出栈的顺序为D->C->B->A;
「递归」：为什么没有停止条件的递归会造成栈溢出?比如函数A为递归函数，不断地调用自己(因为函数还没有执行完，不会把函数弹出栈)，不停地把相同的函数A压入栈，最后造成「栈溢出」(Stack Overfloat)

3.练习：题目：有6个元素6，5，4，3，2，1按顺序进栈，问下列哪一个不是合法的出栈顺序?

A：5 4 3 6 1 2 (√)
B：4 5 3 2 1 6 (√)
C：3 4 6 5 2 1 (×)
D：2 3 4 1 5 6 (√)

题目所说的按顺序进栈指的不是一次性全部进栈，而是有进有出，进栈顺序为6 -> 5 -> 4 -> 3 -> 2 -> 1。

解析：

A答案：65进栈，5出栈，4进栈出栈，3进栈出栈，6出栈，21进栈，1出栈，2出栈(整体入栈顺序符合654321);
B答案：654进栈，4出栈，5出栈，3进栈出栈，2进栈出栈，1进栈出栈，6出栈(整体的入栈顺序符合654321);
C答案：6543进栈，3出栈，4出栈，之后应该5出栈而不是6，所以错误;
D答案：65432进栈，2出栈，3出栈，4出栈，1进栈出栈，5出栈，6出栈。符合入栈顺序;

「栈常见的操作：」

push(element)：添加一个新元素到栈顶位置;
pop()：移除栈顶的元素，同时返回被移除的元素;
peek()：返回栈顶的元素，不对栈做任何修改(该方法不会移除栈顶的元素，仅仅返回它);
isEmpty()：如果栈里没有任何元素就返回true，否则返回false;
size()：返回栈里的元素个数。这个方法和数组的length属性类似;
toString()：将栈结构的内容以字符串的形式返回。

2.2.封装栈类

「代码实现：」

// 封装栈类 
    function Stack(){ 
      // 栈中的属性 
      this.items =[] 
 
      // 栈的相关操作 
      // 1.push():将元素压入栈 
      //方式一(不推荐)：给对象添加方法，其他对象不能复用 
      // this.push = () => { 
      // } 
       
      //方式二(推荐)：给Stack类添加方法，能够多对象复用 
      Stack.prototype.push = function(element) { 
      // 利用数组item的push方法实现Stack类的pop方法 
        this.items.push(element) 
      } 
 
      // 2.pop():从栈中取出元素 
      Stack.prototype.pop = () => { 
      // 利用数组item的pop方法实现Stack类的pop方法 
        return this.items.pop() 
      } 
 
      // 3.peek():查看一下栈顶元素 
      Stack.prototype.peek = () => { 
        return this.items[this.items.length - 1] 
      } 
 
      // 4.isEmpty():判断栈是否为空 
      Stack.prototype.isEmpty = () => { 
      // 两个小时的教训啊不是this.length(不是Stack对象的length，Stack类没有length属性啊)，而是           Stack类中定义的数组items才有length属性呀 
        return this.items.length == 0  
      } 
 
      // 5.size():获取栈中元素的个数 
      Stack.prototype.size = () => { 
        return this.items.length 
      } 
 
      // 6.toString():以字符串形式输出栈内数据 
      Stack.prototype.toString = () => { 
        //希望输出的形式：20 10 12 8 7 
        let resultString = '' 
        for (let i of this.items){ 
          resultString += i + ' ' 
        } 
        return resultString 
      } 
    }

「测试代码：」

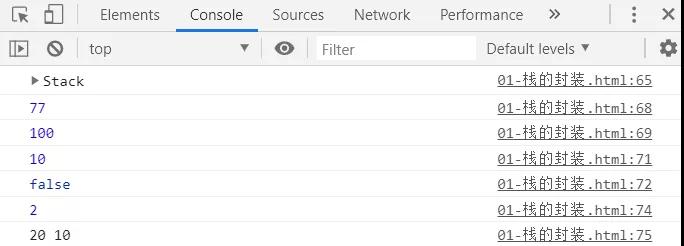
// 栈的使用 
   let  s = new Stack() 
   s.push(20) 
   s.push(10) 
   s.push(100) 
   s.push(77) 
   console.log(s)                                                   //65 
 
   console.log(s.pop());                                            //68 
   console.log(s.pop());                                            //69 
    
   console.log(s.peek());                                           //71 
console.log(s.isEmpty());                                       //72 
   
   console.log(s.size());                                           //74 
   console.log(s.toString());                                       //75

「测试结果：」

image-20200305205050816

「栈结构的简单应用：」

利用栈结构的特点封装十进至转换为二进至的函数：

//简单应用： 
    //封装函数：将十进制转成二进制(十转二的运算最后倒叙取余的特点符合栈'先进后出') 
    let dec2bin = decNumber => { 
      //1.定义一个栈对象，保存余数 
      var  stack = new Stack() 
 
      // 2.循环操作 
      while(decNumber > 0){ 
        // 2.1.获取余数并放入栈中 
        stack.push(decNumber % 2) 
        // 2.2.获取整除后的结果作为下一次运算的数字(floor:向下取整) 
        decNumber = Math.floor(decNumber / 2) 
      } 
 
      // 3.从栈中取出0和1 
      let  binaryString = ''; 
      let a = stack.items.length 
     while(stack.items.length != 0){ 
        binaryString += stack.pop(); 
      } 
      return binaryString; 
    } 
     
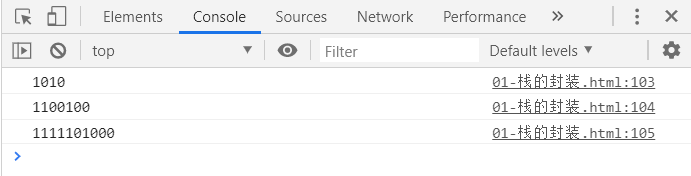
    //测试代码 
    console.log(dec2bin(10));                                       //103 
    console.log(dec2bin(100));                                      //104 
    console.log(dec2bin(1000));                                     //105

「测试结果：」

image-20200305205547226