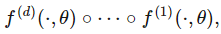神经网络力量背后的证据
从字面上看，通用近似定理是神经网络起作用的理论基础。 简而言之，它声明了一个神经网络，其中具有一个包含足够但有限数量的神经元的隐藏层，可以在激活函数的某些条件下(即，它们必须像S型一样)以合理的精度近似任何连续函数。
由George Cybenko于1989年制定，仅适用于S型曲线激活，并于1991年由Kurt Hornik证明适用于所有激活函数(神经网络的体系结构而不是功能的选择是性能背后的驱动力)，它的发现是一个重要的驱动力 促使神经网络的激动人心的发展成为当今使用它们的众多应用程序。
然而，最重要的是，该定理令人惊讶地解释了为什么神经网络似乎表现得如此聪明。 理解它是发展对神经网络的深刻理解的关键一步。
更深入的探索
紧凑(有界，封闭)集合上的任何连续函数都可以通过分段函数来近似。 以-3和3之间的正弦波为例，可以很令人信服地用三个函数(两个二次函数和一个线性函数)近似。
> Graphed in Desmos.
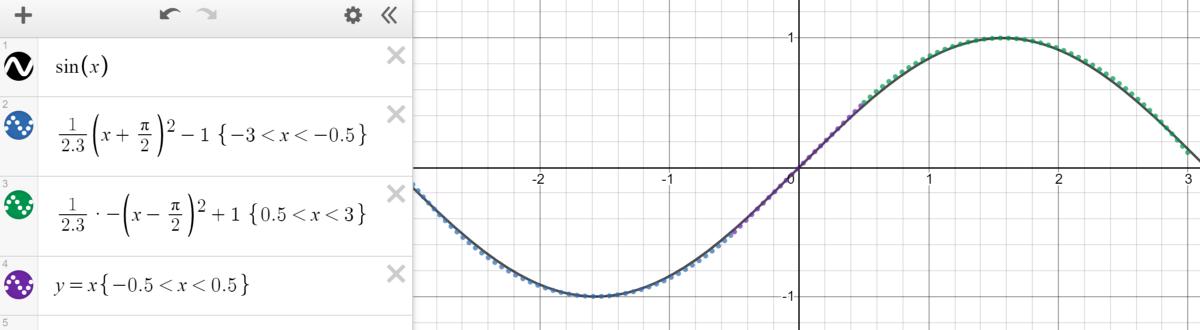
Cybenko对于此分段函数更为具体，因为它可以是恒定的，基本上由适合该函数的几个步骤组成。 有了足够的恒定区域("步长")，就可以在给定的范围内合理估计函数。
> Graphed in Desmos.
基于这种近似，可以通过将每个神经元委托给一个"步骤"来构建网络。 使用权重和偏差作为"门"来确定哪个输入下降，从而确定哪个神经元应该被激活，具有足够数量神经元的神经网络可以简单地将一个函数分为几个恒定区域来估计一个函数。
对于落入神经元委托区域的输入，通过将权重分配到巨大的值，最终值将接近1(使用S型函数进行评估时)。 如果未落入该部分，则将权重移向负无穷大将产生接近0的最终结果。使用S形函数作为各种"处理器"来确定神经元的存在程度，几乎可以近似任何函数 完美地给出了丰富的神经元。 在多维空间中，Cybenko推广了这种想法，每个神经元"控制"多维函数中的空间超立方体。
通用逼近定理的关键在于，与其在输入和输出之间创建复杂的数学关系，不如使用简单的线性操作将复杂的功能划分为许多小的，较不复杂的部分，每个部分都由一个神经元获取。
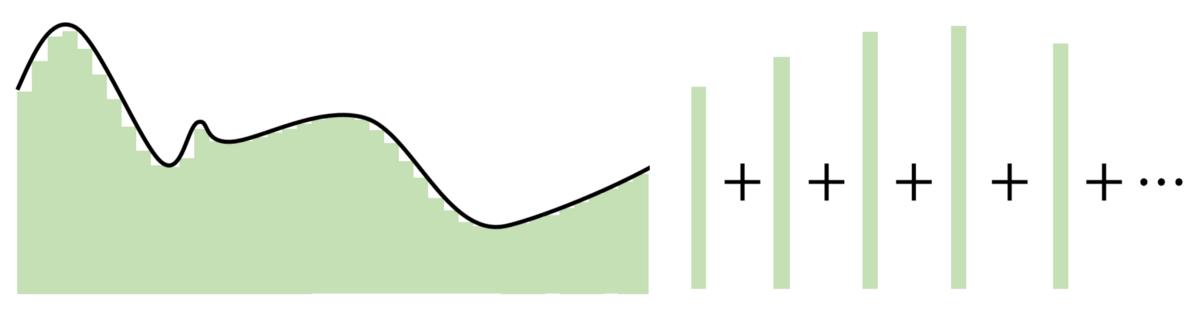> Image created by Author.自Cybenko的初步证明以来，已经做出了许多其他改进，例如针对不同的激活函数(例如ReLU)(无边(在一侧)或具有各种体系结构(递归，卷积等)测试通用逼近定理)。
无论如何，所有这些探索都围绕着一个想法-神经网络在数字上找到了优势。 每个神经元监视特征空间的一个模式或区域，其大小取决于网络中神经元的数量。 神经元越少，每个人需要监视的空间就越大，因此逼近能力会下降。 但是，有了更多的神经元，无论激活功能如何，任何功能都可以与许多小片段结合在一起。
泛化与外推
有人可能会指出，尽管如此简单，但通用近似定理有点太简单了(至少是概念)。 强大的神经网络实际上可以是一个复杂的近似器，它可以分离数字，产生音乐，并且通常表现得很聪明。
神经网络的目的是在给定数据点采样的情况下概括或建模复杂的数学函数。 它们是很好的近似值，但是一旦您请求输入的值超出训练有素的直接范围，它就会惨遭失败。 这类似于有限的泰勒级数逼近法，该方法令人信服地对一定范围内的正弦波进行建模，但在其外部产生了混乱。
> Graphed in Desmos.
外推或在给定训练范围之外做出合理预测的能力并不是神经网络的设计目标。 从通用逼近定理中，我们了解到神经网络根本不是真正的智能，而只是隐藏在多维伪装下的良好估计量，这使其功能(在两三个维度上看起来很普通)似乎令人印象深刻。
神经网络是否在受过训练的范围之外发生故障并不重要，因为那不是其目标。
定理的实际含义
由机器学习工程师的直觉和经验来构造适合给定问题的神经网络体系结构，以便在知道存在这样的网络的情况下，可以很好地近似多维空间，还可以平衡计算账单的真实性。 是。 该定理让机器学习工程师知道总会有一个解决方案。
