从决策树到神经网络
TL; DR:熵是对系统中混沌的一种度量。 因为它比诸如准确性甚至均方误差之类的其他更严格的度量标准更具动态性,所以使用熵来优化从决策树到深度神经网络的算法已显示出可以提高速度和性能。
它在机器学习中无处不在:从决策树的构建到深度神经网络的训练,熵是机器学习中必不可少的度量。
熵源于物理学-它是系统中无序或不可预测性的量度。 例如,在一个盒子里考虑两种气体:一开始,系统的熵很低,因为这两种气体是完全可分离的。 但是,一段时间后,气体混合在一起,系统的熵增加。 有人说,在一个孤立的系统中,熵永远不会减小,没有外力,混沌就不会减弱。
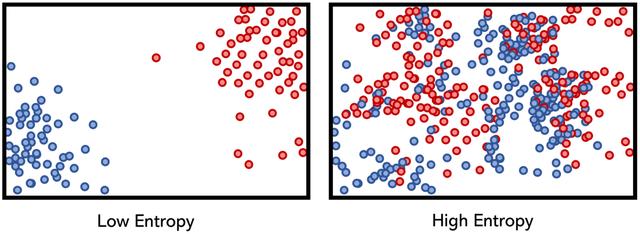
例如,考虑一次抛硬币-如果抛硬币四次而发生事件[尾巴,头,头,尾]。 如果您(或机器学习算法)要预测下一次硬币翻转,则可以确定地预测结果-系统包含高熵。 另一方面,具有事件[尾巴,尾巴,尾巴,尾巴]的加权硬币的熵极低,并且根据当前信息,我们几乎可以肯定地说下一个结果将是尾巴。
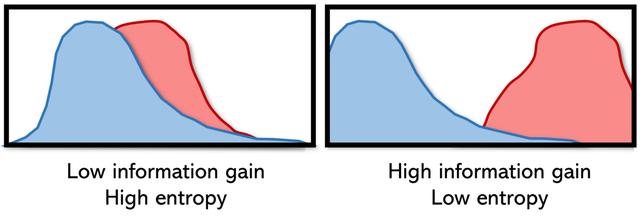
适用于数据科学的大多数情况都介于天文学的高熵和极低的熵之间。 高熵意味着低信息增益,而低熵意味着高信息增益。 可以将信息获取视为系统中的纯净性:系统中可用的纯净知识量。
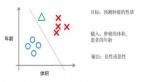
决策树在其构造中使用熵:为了尽可能有效地将一系列条件下的输入定向到正确的结果,将熵较低(信息增益较高)的特征拆分(条件)放在树上较高位置。
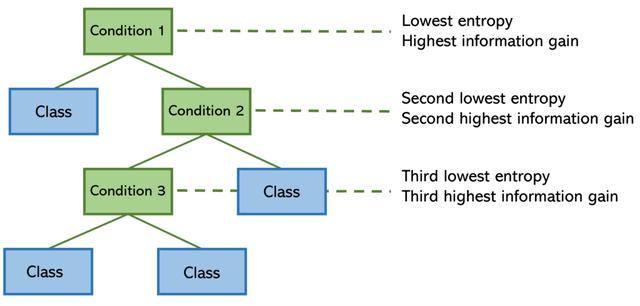
为了说明低熵条件和高熵条件的概念,请考虑假设类特征,其类别用颜色(红色或蓝色)标记,而拆分用垂直虚线标记。
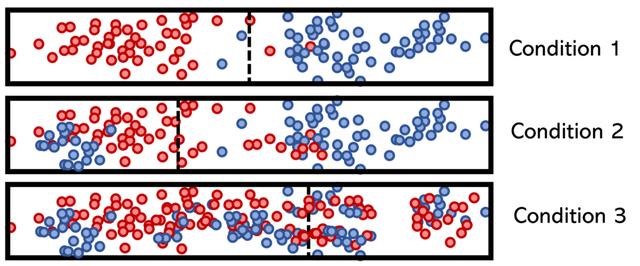
决策树计算特征的熵并对其进行排列,以使模型的总熵最小(并使信息增益比较大)。 从数学上讲,这意味着将最低熵条件放在顶部,以便它可以帮助降低其下方的拆分节点的熵。
决策树训练中使用的信息增益和相对熵定义为两个概率质量分布p(x)和q(x)之间的"距离"。 也称为Kullback-Leibler(KL)散度或Earth Mover的距离,用于训练对抗性网络以评估生成的图像与原始数据集中的图像相比的性能。
神经网络最喜欢的损失函数之一是交叉熵。 无论是分类的,稀疏的还是二进制的交叉熵,该度量标准都是高性能神经网络的默认损耗函数之一。 它也可以用于几乎所有分类算法的优化,例如逻辑回归。 像熵的其他应用(例如联合熵和条件熵)一样,交叉熵是对熵进行严格定义的多种口味之一,适合于独特的应用。
像Kullback-Lieber发散(KLD)一样,交叉熵也处理两个分布p和q之间的关系,分别表示真实分布p和近似分布q。 但是,KLD衡量两个分布之间的相对熵,而交叉熵衡量两个分布之间的"总熵"。
度量定义为使用模型分布q对来自分布p的源的数据进行编码所需的平均位数。 如果考虑目标分布p和近似值q,我们希望减少使用q而不是p表示事件所需的位数。 另一方面,相对熵(KLD)衡量从分布q中的p表示事件所需的额外位数。
交叉熵似乎是衡量模型性能的一种回旋方式,但是有几个优点:
- 基于准确性/错误的指标存在多个问题,包括对训练数据顺序的极端敏感性,不考虑置信度,并且对可能导致错误结果的各种数据属性缺乏鲁棒性。 它们是非常粗略的绩效指标(至少在培训期间)。
- 交叉熵可以衡量信息内容,因此比简单强调所有复选框的度量标准更具动态性和可靠性。 预测和目标被视为分布,而不是等待回答的问题列表。
- 它与概率的性质密切相关,并且特别适用于S型和SoftMax激活(即使它们仅用于最后一个神经元),有助于减少消失的梯度问题。 逻辑回归可以视为二进制交叉熵的一种形式。
尽管熵并不总是最佳的损失函数(尤其是在目标函数p尚未明确定义的情况下),但熵通常表现为性能增强,这说明了熵在任何地方都存在。
通过在机器学习中使用熵,它的核心组成部分(不确定性和概率)可以通过交叉熵,相对熵和信息增益等思想得到很好的体现。 熵对于处理未知数非常明确,这在模型构建中非常需要。 当模型在熵上进行优化时,它们能够以增强的知识和目标意识在不可预测的平原上徘徊。