在R、Python和Julia中常用的数据可视化技术

俗话说“一图胜千言”。通过各种图片和图形化展示，我们可以更清晰地表达很多抽象概念、理论、数据模式或某些想法。在本章中，我们首先解释为什么应该关心数据可视化。然后，我们将讨论几种在R、Python和Julia中常用的数据可视化技术。此外，我们还将介绍几个特殊主题，例如如何生成图形、饼图和条形图，如何添加标题、趋势线、希腊字母，以及如何输出图形。在本章的最后，我们将讨论一个可选话题，即动态表示以及如何将它们保存为HTML文件。

本章包含以下主题：

• 数据可视化的重要性
• R数据可视化
• Python数据可视化
• Julia数据可视化

1. 数据可视化的重要性

对于数据科学和商业分析领域的用户或研究人员来说，使用各种类型的图形、饼图、条形图以及其他视觉手段展示数据中隐含的潜在趋势或模式对理解数据至关重要，同时能够帮助研究人员更好地向观众或客户呈现数据。这样做主要有以下几个原因。

第一，语言有时很难描述我们的发现，尤其是存在几种模式或诸多影响因素时，通过几个单独的图形和一个连接图则可以更好地理解和解释复杂的关系。

第二，我们可以使用图形或图片来解释某些算法，例如二分法（参见4.9节）。

第三，我们也可以使用相对大小来表示不同的含义。在金融领域，一个基本概念叫作货币时间价值（Time Value of Money，TVM），意思是“一鸟在手胜过双鸟在林”。今天的100美元比同等数额的未来现金流更有价值。通过不同尺寸的不同圆圈表示发生在未来不同时间点上的现金流的现值，可以帮助读者更清楚地理解这个概念。

第四，我们的数据可能非常混乱，所以简单地展示数据点可能会使读者更加困惑。如果我们能用一个简单的图形来展示它的主要特征、属性或模式将大有益处。

2. R数据可视化

首先，我们来看R中最简单的图形。利用下面一行R代码，我们画出了从

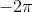
到

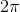
范围内的余弦函数值：

> plot(cos,-2*pi,2*pi) 

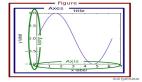
对应的图形如图4.1所示。

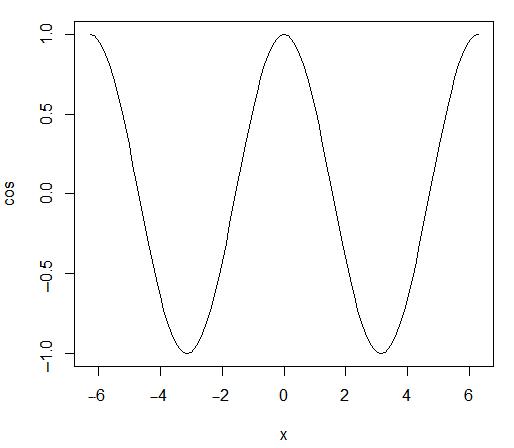
图4.1　余弦函数图

直方图也有助于我们理解数据点的分布。图4.1就是一个简单的例子。首先，我们生成一组服从标准正态分布的随机数。为了便于说明，第一行的set.seed()命令其实是多余的，它的存在将保证所有使用相同seed值（本例中为333）的用户将得到相同的随机数集合。

换句话说，在输入值相同的情况下，直方图看起来将是一样的。在下一行中，rnorm(n)函数画出了n个服从标准正态分布的随机数。接着，最后一行使用hist()函数生成一个直方图：

> set.seed(333) 
> data<-rnorm(5000) 
> hist(data) 

相关直方图如图4.2所示。

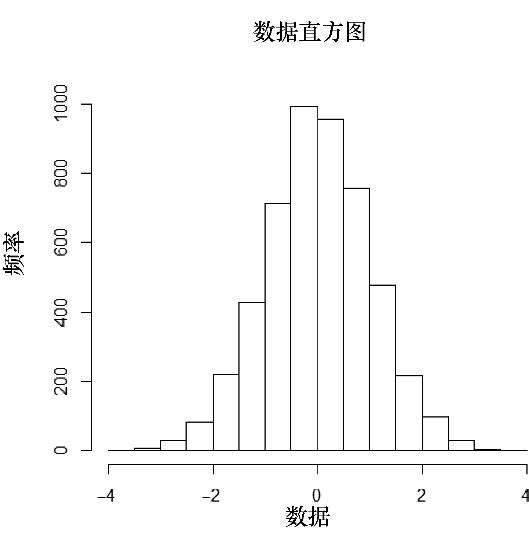
图4.2　示例直方图

注意，代码rnorm(5000)与rnorm(5000,mean=0,sd=1)相同，其中含义为均值的默认值为0，sd的默认值为1。下一个R程序将为标准正态分布左侧的尾巴填充阴影：

x<-seq(-3,3,length=100) 
y<-dnorm(x,mean=0,sd=1) 
title<-"Area under standard normal dist & x less than -2.33" 
yLabel<-"standard normal distribution" 
xLabel<-"x value" 
plot(x,y,type="l",lwd=3,col="black",main=title,xlab=xLabel,ylab=yLabel) 
x<-seq(-3,-2.33,length=100) 
y<-dnorm(x,mean=0,sd=1) 
polygon(c(-4,x,-2.33),c(0,y,0),col="red") 

相关图形如图4.3所示。

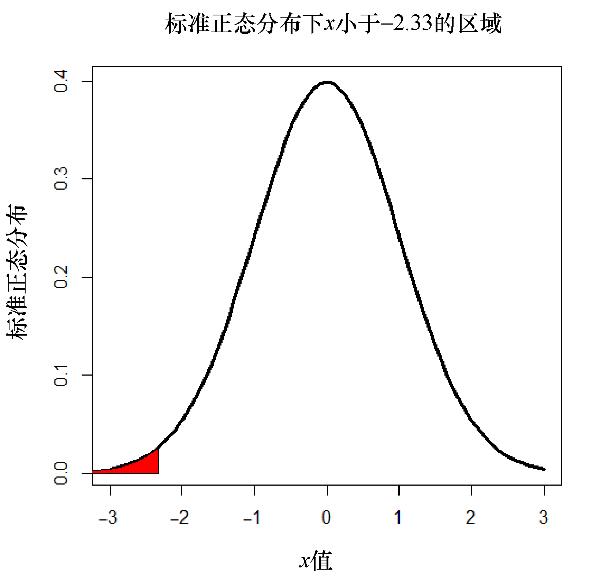
图4.3　标准正态分布示例图

注意，根据上面代码中的最后一行可知，阴影区域为红色。

在探索各种数据集的属性方面，R包rattle非常有用。如果rattle包没有预先安装，那么我们可以运行以下代码安装它：

> install.packages("rattle") 

然后，运行以下代码启动它：

> library(rattle) 
> rattle() 

单击回车键后，可以看到图4.4中的结果。

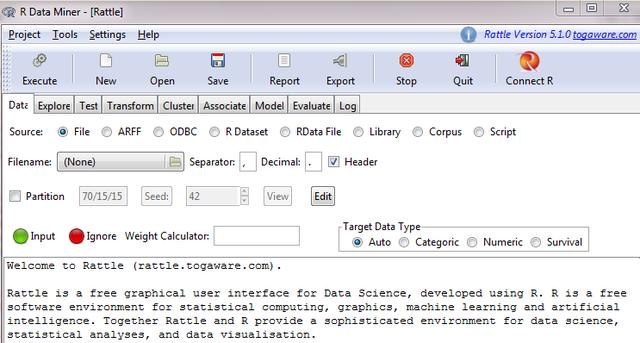
图4.4　Rattle包启动界面

首先，我们需要导入某些数据集。我们从7种可能的格式中选择数据源，如文件、 ARFF、ODBC、R数据集和RData文件，并且可以从此处加载数据。

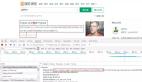
最简单的方法是使用Library选项，它将列出rattle包中所有内嵌的数据集。单击Library后，我们可以看到内嵌数据集的列表。假设单击左上角的Execute后我们选择了acme:boot:Monthly Excess Returns，那么我们将看到图4.5中的界面。

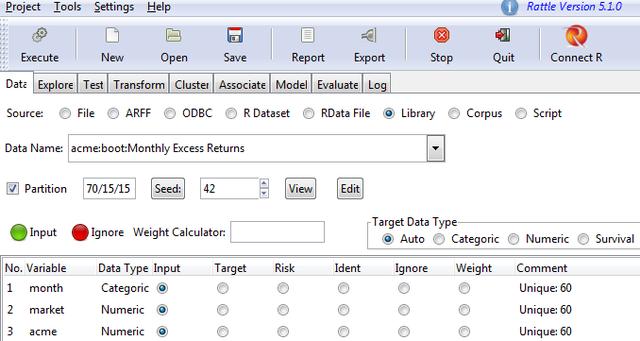
图4.5　导入数据集界面

现在，我们就可以研究数据集的属性了。点击Explore后，我们可以使用各种图形来查看数据集。假设我们选择Distribution，并勾选Benford复选框，那么我们就可以参考图4.6来了解更多细节。

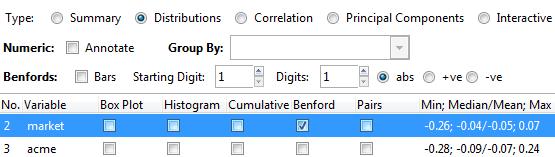
图4.6　查看数据集属性信息

单击Execute之后，将弹出图4.7所示内容。图4.7上方的红线显示了根据本福特定律（Benford Law）算出的1～9每个数字的频率，而底部的蓝线则展示了数据集的属性。请注意，如果你的计算机系统中还没有安装reshape包，则此命令要么无法运行，要么会请求许可将该包安装到你的计算机上。

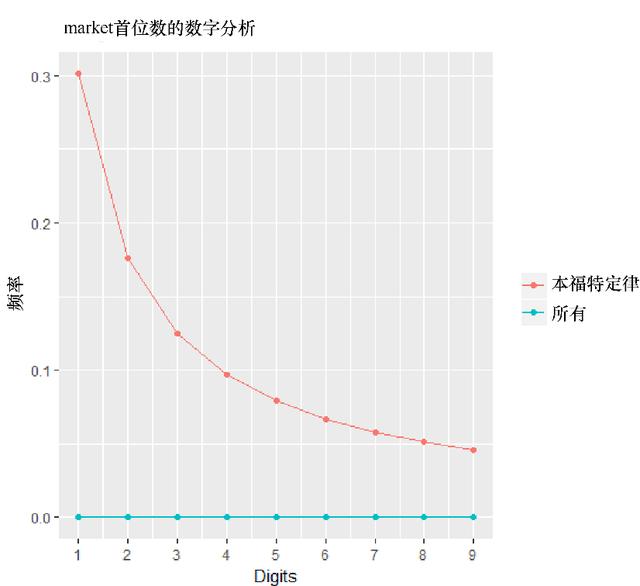
图4.7　数据集的Benford定律符合情况

在图4.7中，两条线之间的巨大差异表明我们的数据不符合本福特定律建议的分布规律。在现实世界中，我们知道很多人、事件和经济活动是相互关联的，使用各种图形来展示这样一个多节点、相互连接的图像是一个很好的办法。如果没有预装qgraph包，那么用户必须运行以下程序来安装它：

> install.packages("qgraph") 

下一个程序展示了从a到b、a到c等节点之间的连接：

library(qgraph) 
stocks<-c("IBM","MSFT","WMT") 
x<-rep(stocks, each = 3) 
y<-rep(stocks, 3) 
correlation<-c(0,10,3,10,0,3,3,3,0) 
data <- as.matrix(data.frame(from =x, to =y, width =correlation)) 
qgraph(data, mode = "direct", edge.color = rainbow(9)) 

如果将数据展示出来，该程序的意义就会更加清晰。相关性展示出这些股票之间联系的紧密程度。注意，所有这些值都是随机选择的，并没有现实意义。

> data 
　　 from　 to　　　 width 
[1,] "IBM"　"IBM"　 " 0" 
[2,] "IBM"　"MSFT"　"10" 
[3,] "IBM"　"WMT"　 " 3" 
[4,] "MSFT" "IBM"　 "10" 
[5,] "MSFT" "MSFT"　" 0" 
[6,] "MSFT" "WMT"　 " 3" 
[7,] "WMT"　"IBM"　 " 3" 
[8,] "WMT"　"MSFT"　" 3" 
[9,] "WMT"　"WMT"　 " 0" 

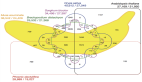
第3个变量的值越大表明前面两个变量的相关性越强。例如，IBM与MSFT的相关性更强（值为10），大于IBM与WMT的相关性（值为3）。图4.8展示了这3只股票的相关性强弱程度。

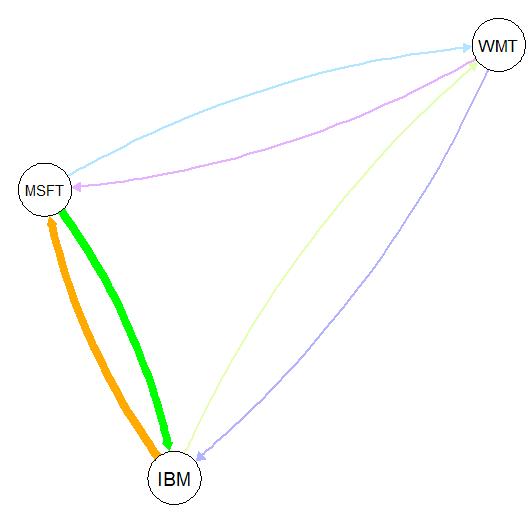
图4.8　IBM、MSFT和WMT股票的相关性强弱程度

以下程序展示了5个因素之间的关系或相互联系：

library(qgraph) 
data(big5) 
data(big5groups) 
title("Correlations among 5 factors",line = 2.5) 
qgraph(cor(big5),minimum = 0.25,cut = 0.4,vsize = 1.5, 
　　groups = big5groups,legend = TRUE, borders = FALSE,theme = 'gray') 

相关图形如图4.9所示。

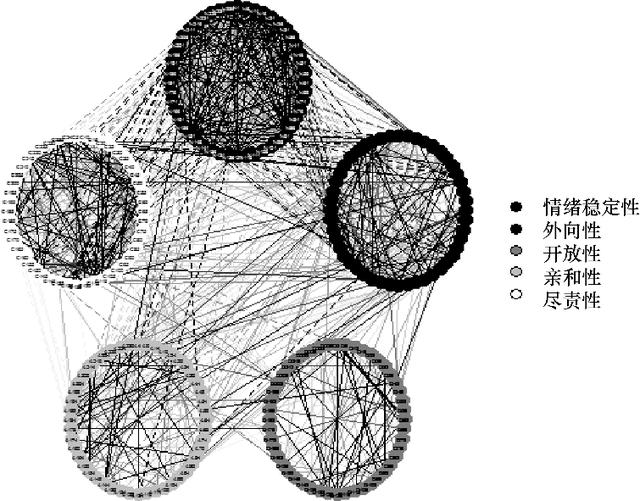
图4.9　5个因素之间的相互联系

3. Python数据可视化

Python中图形和图像方面使用最广泛的包是matplotlib。下面的程序仅仅包含3行代码，所以可以看作是最简单的生成一个图形的Python程序：

import matplotlib.pyplot as plt 
plt.plot([2,3,8,12]) 
plt.show() 

第一行命令会上传一个名为matplotlib.pyplot的Python包，并将其重命名为plt。

注意，我们甚至可以使用其他简短的名称，但通常使用plt表示matplotlib包。第二行绘制了4个点，最后一行总结了整个过程。完整图形如图4.10所示。

在下一个例子中，我们为x和y添加了标签，以及一个标题。所使用的函数是余弦函数，其中输入值范围为

～

。

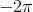
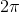
import scipy as sp 
import matplotlib.pyplot as plt 
x=sp.linspace(-2*sp.pi,2*sp.pi,200,endpoint=True) 
y=sp.cos(x) 
plt.plot(x,y) 
plt.xlabel("x-value") 
plt.ylabel("Cosine function") 
plt.title("Cosine curve from -2pi to 2pi") 
plt.show() 

图4.10　matplotlib包生成的图形示例

漂亮的余弦曲线如图4.11所示。

如果我们今天收到100美元，它将比两年后收到的更有价值，这个概念叫作货币时间价值，因为我们现在可以将100美元存入银行来赚取利息。下面的Python程序使用size来说明此概念。

import matplotlib.pyplot as plt 
fig = plt.figure(facecolor='white') 
dd = plt.axes(frameon=False) 
dd.set_frame_on(False) 
dd.get_xaxis().tick_bottom() 
dd.axes.get_yaxis().set_visible(False) 
x=range(0,11,2) 
x1=range(len(x),0,-1) 
y = [0]*len(x); 
plt.annotate("$100 received 
today",xy=(0,0),xytext=(2,0.15),arrowprops=dict(facecolor='black',shrink=2)) 
plt.annotate("$100 received in 2 
years",xy=(2,0),xytext=(3.5,0.10),arrowprops=dict(facecolor='black',shrink= 
2)) 
s = [50*2.5**n for n in x1]; 
plt.title("Time value of money ") 
plt.xlabel("Time (number of years)") 
plt.scatter(x,y,s=s); 
plt.show() 

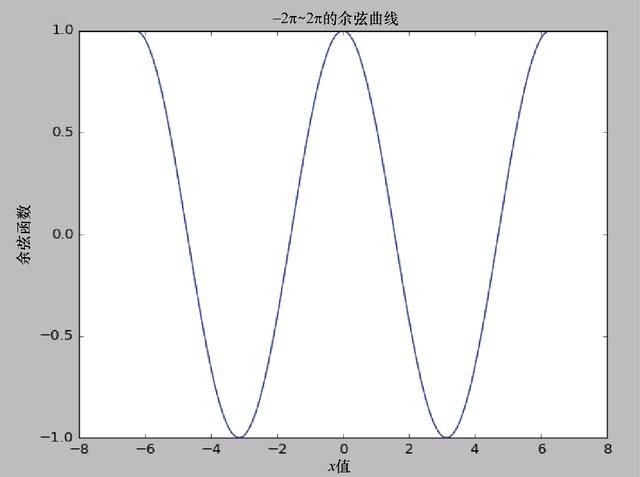
图4.11　为图形添加x和y轴标签及标题

相关的图形如图4.12所示。同样，不同尺寸表示它们现值的相对大小。

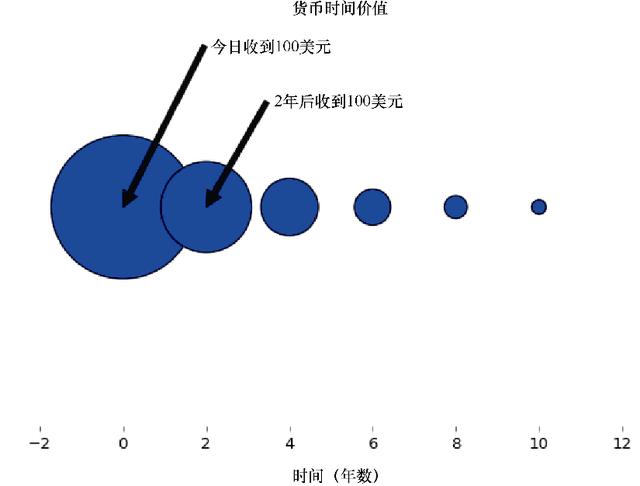
图4.12　货币时间价值概念解释

4. Julia数据可视化

对于下面的Julia程序，我们使用了一个名为Plots的包，用于安装此包的命令为Pkg.add("Plots")。这里，我们通过一个Jupyter notebook运行Julia程序。图4.13展示了一个Julia程序。

图4.13　Julia程序

单击菜单栏上的Kernel项目，然后单击Restart and Run All，我们得到图4.14所示的结果。

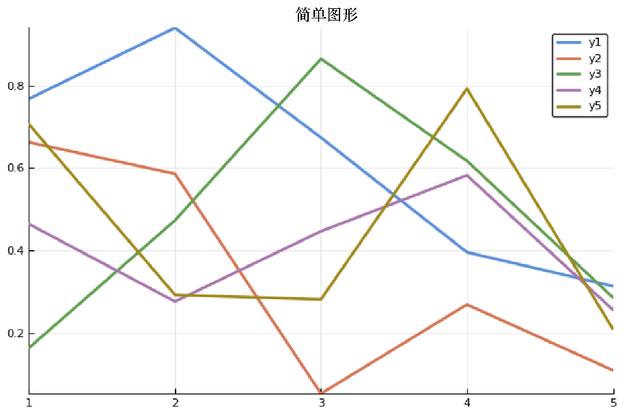
图4.14　运行结果图

同样地，srand(123)命令保证使用相同随机种子的任何用户都会得到相同的随机数集合。为此，用户会得到与前面相同的图形。下一个例子是使用Julia包PyPlot绘制的散点图。

using PyPlot 
n=50 
srand(333) 
x = 100*rand(n) 
y = 100*rand(n) 
areas = 800*rand(n) 
fig = figure("pyplot_scatterplot",figsize=(10,10)) 
ax = axes() 
scatter(x,y,s=areas,alpha=0.5) 
title("using PyPlot: Scatter Plot") 
xlabel("X") 
ylabel("Y") 
grid("on") 

相关图形如图4.15所示。

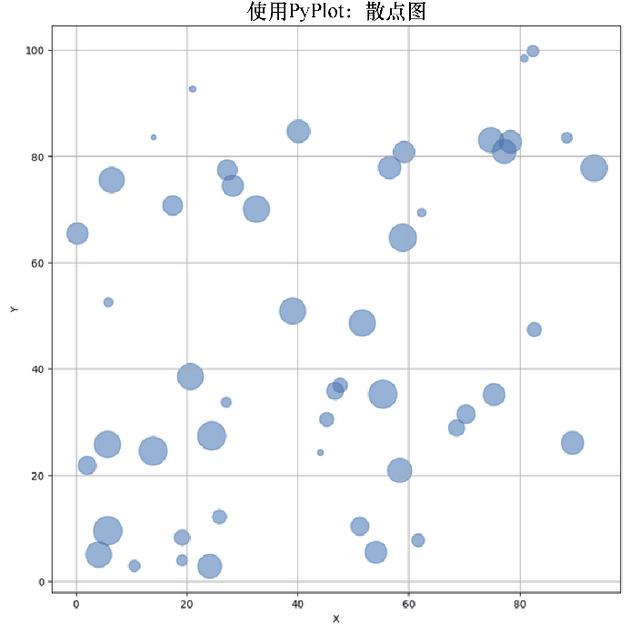
图4.15　Julia包PyPlot绘制散点图示例

下一个Julia程序借鉴自Sargent和Stachurski的程序。

using QuantEcon: meshgrid 
using PyPlot:surf 
using Plots 
n = 50 
x = linspace(-3, 3, n) 
y = x 
z = Array{Float64}(n, n) 
f(x, y) = cos(x^2 + y^2) / (1 + x^2 + y^2) 
for i in 1:n 
　　for j in 1:n 
　　　　z[j, i] = f(x[i], y[j]) 
　　end 
end 
xgrid, ygrid = meshgrid(x, y) 
surf(xgrid, ygrid, z',alpha=0.7) 

令人印象深刻的图形如图4.16所示。

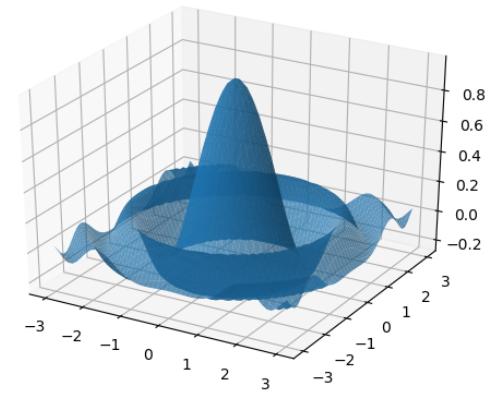
图4.16　Sargent和Stachurski程序结果图