递归是一个神奇的算法,它是编程书籍中讲解的最尴尬部分。这些书籍通常会展示一个递归的阶乘实现,然后警告你,虽然它能运行但是它非常的慢并且可能会堆栈溢出而崩溃。虽然大家对它持怀疑态度,但是这不影响递归是算法中最强大的想法。
让我们来看看经典的递归阶乘:
factorial.c
- #include <stdio.h>
- int factorial(int n)
- {
- int previous = 0xdeadbeef;
- if (n == 0 || n == 1) {
- return 1;
- }
- previous = factorial(n-1);
- return n * previous;
- }
- int main(int argc)
- {
- int answer = factorial(5);
- printf("%d\n", answer);
- }
一个函数调用自身的想法起初非常神秘。为了解释整个过程,下图展示了factorial(5)被调用到n == 1 栈上结构。
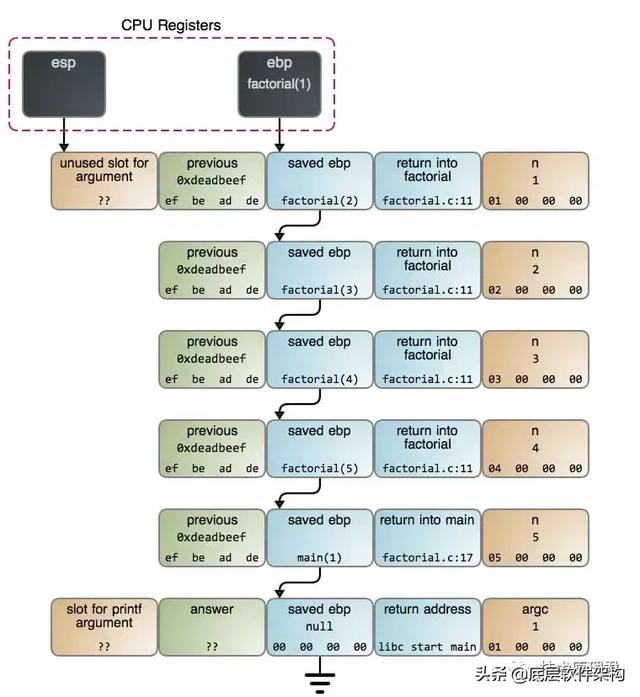
每次调用factorial都会生成一个新的栈帧。这些栈帧的创建和销毁使得递归因子比其迭代部分慢。在调用开始和返回之前的这些栈帧累积是可能耗尽栈空间并使程序崩溃。
但是这些担忧通常是理论上的。例如,栈帧 factorial每个占用16个字节(这可以根据栈对齐和其他因素而变化)。如果您在计算机上运行现代x86 Linux内核,通常默认有8兆字节的堆栈空间,因此factorial n最多可以处理512,000。这是一个巨大数,需要8,971,833位来表示这个数,所以栈空间是我们问题中最少的:一个微弱的整数 - 甚至是64位 - 在我们用完栈空间之前会溢出数万次。
我们稍后会看一下CPU的使用情况,但是现在让我们从位和字节中退一步,看看递归作为一种通用技术。我们的阶乘算法归结为将整数N,N-1,... 1推入堆栈,然后以相反的顺序将它们相乘。我们使用程序的调用堆栈执行此操作的前提是:我们可以在堆上分配堆栈并使用它。虽然调用堆栈确实具有特殊属性,但它只是您可以使用的另一种数据结构。
一旦你看到调用堆栈作为一个数据结构,其他东西就变得豁然开朗了:将本身之前所有这些整数累加起来再乘以自身这显然不是明智的选择。 使用迭代过程计算阶乘更为明智。
有一个传统的面试问题,在迷宫中放一只老鼠,你帮助老鼠找奶酪,假设老鼠可以在迷宫中向左或向右转。你会如何建模并解决这个问题?
像生活中的大多数问题一样,你可以将这种啮齿动物的任务抽象到一个图形,特别是一个二叉树,其中节点代表迷宫中的位置。然后你可以尽可能地让鼠标左转,当它到达死胡同时回溯然后右转。下图就是老鼠路径 :
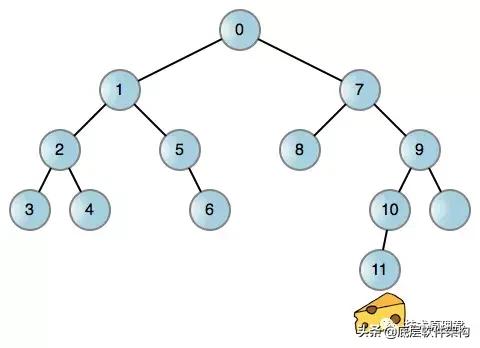
每条边(线)都可以左转或右转,老鼠可以选择。如果任一转弯被阻止,则相应的边缘不存在。无论您使用调用堆栈还是其他数据结构,此过程本质上都是递归的。但使用调用栈非常简单:
Maze.c
- #include <stdio.h>
- #include "maze.h"
- int explore(maze_t *node)
- {
- int found = 0;
- if (node == NULL) {
- return 0;
- }
- if (node->hasCheese) {
- return 1; // found cheese
- }
- found = explore(node->left) || explore(node->right);
- return found;
- }
- int main(int argc)
- {
- int found = explore(&maze);
- }
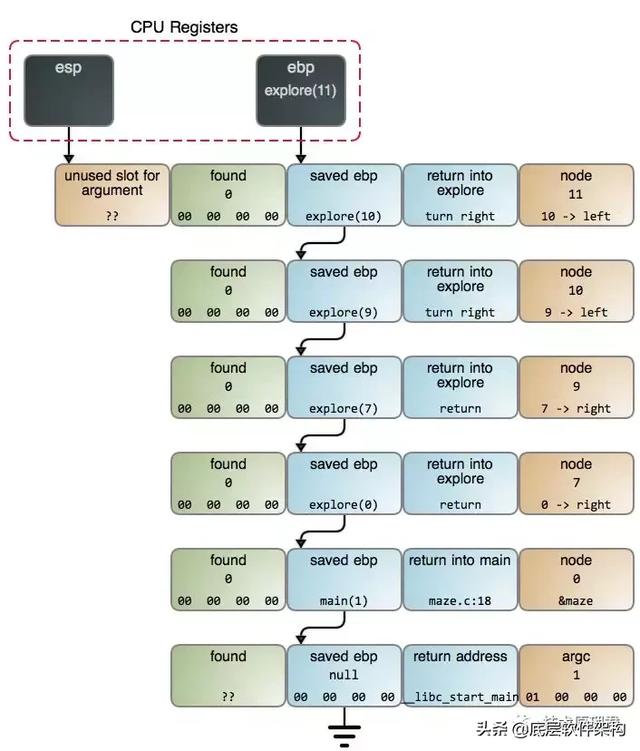
在maze.c:13中找到奶酪,下图是堆栈。
虽然这里很难摆脱递归,但这并不意味着它必须通过调用栈来完成。例如,你可以使用一个字符串 RRLL来跟踪转弯,并依靠字符串来决定鼠标的下一步行动。或者你可以分配其他变量来记录奶酪寻找的状态。你仍然在实现递归过程,但滚动你自己的数据结构。
这可能会更复杂,因为调用堆栈就像手套一样。每个堆栈帧不仅记录当前节点,还记录该节点中的计算状态(在这种情况下,我们是仅采用左侧还是已经尝试右侧)。然而,我们有时会因为害怕溢出而放弃了美好的东西。在我看来是非常愚蠢的。
正如我们所看到的,栈很大,并且在栈空间之前经常会遇到其他约束。还可以检查问题的大小并确保可以安全地处理。CPU担心主要是由两个广泛的病理学例子灌输:愚蠢的因子和可靠的O(2 n) 递归Fibonacci没有记忆。这些并不表示理智的堆栈递归算法。
现实情况是栈操作很快。数据的偏移是准确的,栈在缓存中,不需要冷启动,并且有专门的指令来完成工作。同时,使用您自己的堆分配数据结构会产生大量开销。会看到其他人编写的东西比调用堆栈递归更复杂,性能更差。
现代CPU 非常优秀了,通常不是瓶颈。简单往往和性能等同。