前言
百度百科搜索“机器学习”,映入眼帘的是我无法企及的高度:
- 机器学习是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。
让我在怀疑自己智商的同时也在思考:这段话除了阐述了机器学习很牛X,能够模拟人类学习行为以外,好像并没有让我明白这四个词的含义,反而加重了我的思想负担,带着我越加沉重的大脑继续往下看,找到了我认为本词条最为重要的定义:

然而并卵!!!
就像是看着笑傲江湖里的《葵花宝典》,由于没有自宫,看了再怎么高深的剑法招式,也只是流于片面,除了牛批,还是牛批。至此我终于明白,原来是打开方式不对,从一开始就错了(要自宫)!
所以,需要换个方式,这一次我们用初中数学打开:
从一次函数说起
在初中的数学中,我们常常遇到类似这样题目:
- 给定平面内的三个点坐标(x,y): A(1,3)、B(2,5)、C(3,7)求x=5时,y的值。
面对如此问题,我们可以先把三个点放到坐标轴上看看,如图:
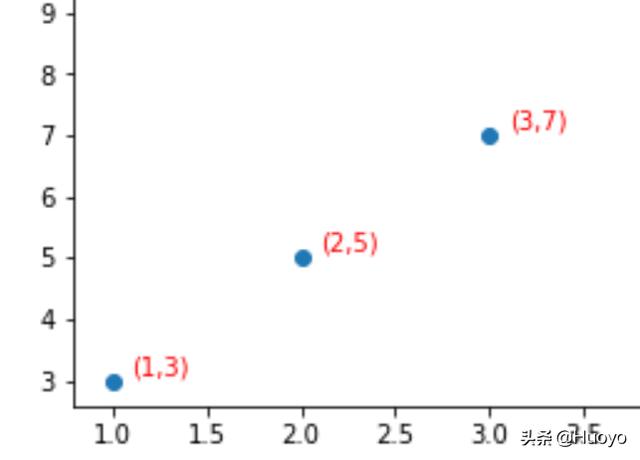
可以发现三个点在一条直线上,符合一次函数的性质,那我们只需要求出这条直线的方程式,将x=5代入方程式,就可以求出此时y的值。
此时,问题就变成了:
- 已知A(1,3)、B(2,5)、C(3,7)三个点,横坐标和纵坐标的关系符合一次函数
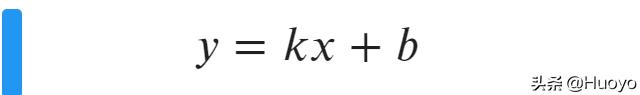
求x=5时,y的值。
问题到此就进入了我初中知识水平的层面,只需要将A、B、C三个点代入y=kx+b得到关于k和b的一个方程组,求解可得:
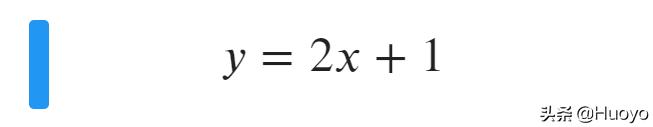
那么x=5时,y等于2*5+1=11(放着我来,这个我会算)。
问题思考
机器学习无非就是类似于上面的一个过程,在给定一定量的输入(x)和输出(y)数据的前提下,找出一个函数来表示这些x和y之间的关系,根据这个函数,我们可以在知道x的条件下轻松求出y,例如我们在网购之后输入评论,系统就能自动识别出是好评还是差评。
上述案例的这个函数我们可以称之为模型,x称之为特征,y就是机器学习要预测的结果,而已知的x和y的组合称之为训练数据,训练的过程也就是找出x和y的关系的过程(而不是用皮鞭抽的过程)。
然而真实的机器学习案例中往往没这么简单,只有一个特征x的函数怎么满足更为复杂的业务需求呢?
“一个不行就两个,两个不行就三个,三个不行还可以加呀,只要给钱,不好意思,扯远了!”
当特征数量为多个,我们依旧可以基于上面的一次函数基础,进行模型假设
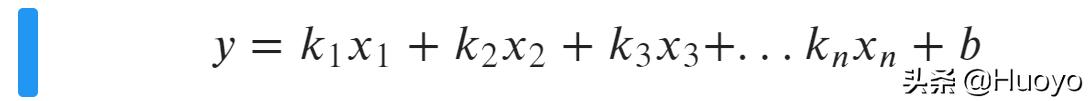
那么问题也可以得到解决,这就是机器学习里面较为基础的线性回归。
如果你觉得这些函数都只能求出一个值,没啥意思,能否帮我识别出评论区里哪些是好评,哪些是差评呢?
“当然是没问题的!只需要把y的结果映射到0-1之间,然后对y进行判断,y>=0.5表示好评,y<0.5表示差评就行,然后这个映射函数我们称之为激活函数,怎么实现的先不管,理解为主”
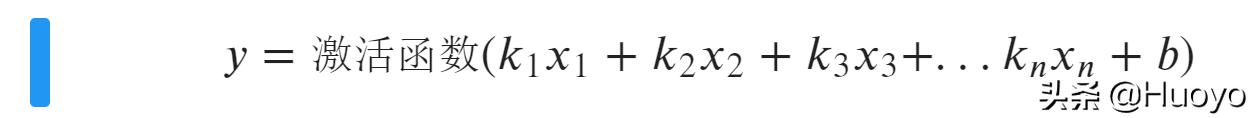
这样就实现了机器学习中分类任务逻辑回归。
如果你觉得一个特征对应一个权重有点low,而且很多事情都并非是线性相关,如何解决这个问题呢?
“一层权重不够,那就加呗,如果再不够,那就再加!”
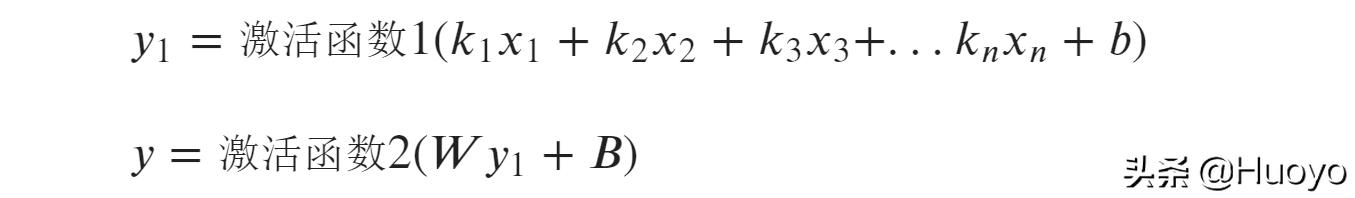
你还要吗?我再加点
上面的过程跑得有点远,一不小心已经到了深度学习的层面,路漫漫其修远兮,我的智商有点跟不上...(所以用省略号代替)
总结
以上案例仅仅是机器学习中监督学习的过程,真正的机器学习往往比这个复杂得多,还分为非监督学习,半监督学习,在此不做多余赘述,有机会再写,再见!

































