相信大家都使用过消息MQ,他可以很好地进行系统解耦,减低变成的复杂度,又可以进行削峰,增加系统在高并发的稳定性。那么使用MQ有哪些注意事项呢?是不是MQ就是万无一失呢?一条MQ消息从产生到消费,有没有可能失败?在哪些环节可能失败,如何处理?
1.消息生产失败
一般来说,从生产者到MQ中间件是通过网络调用的,是网络调用就有可能存在失败。下面这些原因,都有可能造成MQ生产失败,例如网络波动,尽管生产者到MQ服务器之间是内网调用,并不意味着网络调用的成功率就是百分之百,内网调用也会遇到网络波动,造成调用超时或者失败。又如调用的MQ机器瞬间Crash掉,这也是有可能造成调用失败的。 面对生产者调用MQ的失败,我们是容易比较容易处理的 , 我们只要简单地进行重试即可,如果重试2-3次失败,那么非常有可能是出现大问题,这个时候再重试意义不大,需要进行告警并处理。
2.MQ处理存储失败
消息到达消息中间件之后,通常是会被存储起来的,只有被写入到磁盘中,消息才是真正地被存储,不会丢失。但是,大部分MQ中间件并不是收到消息就立马写入磁盘的,只是由于磁盘的写入速度相对于内存,现得慢得多得多,所以,像Kafka这样的消息系统,是会把消息写到缓冲区中,异步写入磁盘,如果机器在中途突然断电,是有可能会丢失消息的。为了解决这个问题,大部分的MQ都是采用 分布式部署, 消息会在多台机器上写入缓存中成功才会返回给业务方成功,由于多台机器同时断电的可能性较低,我们可以认为这是比较低成本又可靠的方案。
3.消费者处理失败
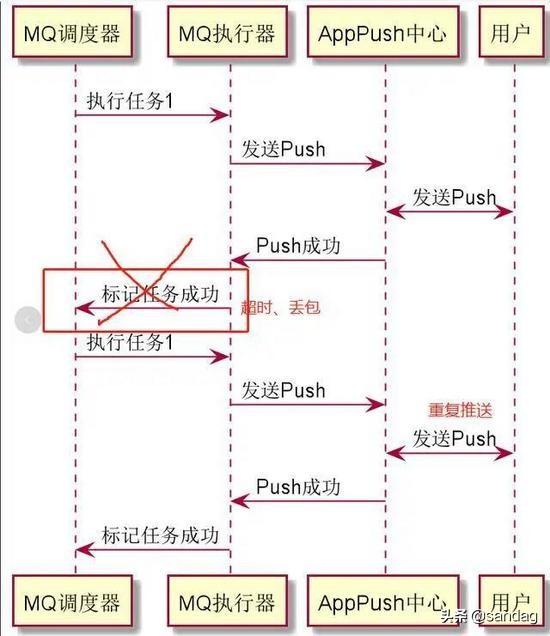
一般的MQ都有MQ重试机制,如果处理失败,就会尝试重复消费这个MQ。这个带来的问题就是,MQ可能已经成功消费了,但是在通知MQ中间件的时候失败了,这个时候带来的结果就是消息重复消费。同理,在生产者重试的时候,也会遇到消息重复消费的问题。这个时候,就要求我们尽量把接口设计得有 幂等性 ,这个时候即便是重复消费,也不用担心什么问题了。基本上做好这三点,我们就能够大大地提高我们地系统地可用性了!
这里需要关注几个重点:
- 幂等不仅仅只是一次(或多次)请求对资源没有副作用(比如查询数据库操作,没有增删改,因此没有对数据库有任何影响)。
- 幂等还包括第一次请求的时候对资源产生了副作用,但是以后的多次请求都不会再对资源产生副作用。
- 幂等关注的是以后的多次请求是否对资源产生的副作用,而不关注结果。
幂等性是系统服务对外一种承诺(而不是实现),承诺只要调用接口成功,外部多次调用对系统的影响是一致的。声明为幂等的服务会认为外部调用失败是常态,并且失败之后必然会有重试。
什么情况下需要幂等
业务开发中,经常会遇到重复提交的情况,无论是由于网络问题无法收到请求结果而重新发起请求,或是前端的操作抖动而造成重复提交情况。 在交易系统,支付系统这种重复提交造成的问题有尤其明显,比如:
用户在APP上连续点击了多次提交订单,后台应该只产生一个订单;
向支付系统发起支付请求,由于网络问题或系统BUG重发,支付系统应该只扣一次钱。 很显然,声明幂等的服务认为,外部调用者会存在多次调用的情况,为了防止外部多次调用对系统数据状态的发生多次改变,将服务设计成幂等。
幂等VS防重
上面例子中遇到的问题,只是重复提交的情况,和服务幂等的初衷是不同的。重复提交是在第一次请求已经成功的情况下,人为的进行多次操作,导致不满足幂等要求的服务多次改变状态。 而幂等更多使用的情况是第一次请求不知道结果(比如超时)或者失败的异常情况下,发起多次请求,目的是多次确认第一次请求成功,却不会因多次请求而出现多次的状态变化。
什么情况下需要保证幂等性
以SQL为例,有下面三种场景,只有第三种场景需要开发人员使用其他策略保证幂等性:
- SELECT col1 FROM tab1 WHER col2=2 ,无论执行多少次都不会改变状态,是天然的幂等。
- UPDATE tab1 SET col1=1 WHERE col2=2 ,无论执行 成功 多少次 状态 都是一致的,因此也是幂等操作。
- UPDATE tab1 SET col1=col1+1 WHERE col2=2 ,每次执行的结果都会发生变化,这种不是幂等的。
为什么要设计幂等性的服务
幂等可以使得客户端逻辑处理变得简单,但是却以服务逻辑变得复杂为代价。 满足幂等服务的需要在逻辑中至少包含两点:
- 首先去查询上一次的执行状态,如果没有则认为是第一次请求
- 在服务改变状态的业务逻辑前,保证防重复提交的逻辑
幂等的不足
幂等是为了简化客户端逻辑处理,却增加了服务提供者的逻辑和成本,是否有必要,需要根据具体场景具体分析, 因此除了业务上的特殊要求外,尽量不提供幂等的接口。
增加了额外控制幂等的业务逻辑,复杂化了业务功能;
把并行执行的功能改为串行执行,降低了执行效率。
保证幂等策略
幂等需要通过 唯一的业务单号 来保证。也就是说相同的业务单号,认为是同一笔业务。使用这个唯一的业务单号来确保,后面多次的相同的业务单号的处理逻辑和执行效果是一致的。 下面以支付为例,在不考虑并发的情况下,实现幂等很简单:
①先查询一下订单是否已经支付过,
②如果已经支付过,则返回支付成功;如果没有支付,进行支付流程,修改订单状态为‘已支付’。
防重复提交策略
上述的保证幂等方案是分成两步的,第②步依赖第①步的查询结果,无法保证原子性的。 在高并发下就会出现下面的情况: 第二次请求在第一次请求第②步订单状态还没有修改为‘已支付状态’的情况下到来。 既然得出了这个结论,余下的问题也就变得简单:把查询和变更状态操作加锁,将并行操作改为串行操作。
乐观锁
如果只是更新 已有 的数据,没有必要对业务进行加锁,设计表结构时使用乐观锁,一般通过version来做乐观锁,这样既能保证执行效率,又能保证幂等。例如: UPDATE tab1 SET col1=1,version=version+1 WHERE version=#version# 不过, 乐观锁存在失效的情况,就是常说的ABA问题,不过如果version版本一直是自增的就不会出现ABA的情况。
防重表
使用订单号orderNo做为去重表的唯一索引,每次请求都根据订单号向去重表中插入一条数据。第一次请求查询订单支付状态,当然订单没有支付,进行支付操作,无论成功与否,执行完后更新订单状态为成功或失败,删除去重表中的数据。后续的订单因为表中唯一索引而插入失败,则返回操作失败,直到第一次的请求完成(成功或失败)。 可以看出防重表作用是加锁的功能。
分布式锁
这里使用的防重表可以使用分布式锁代替,比如Redis。订单发起支付请求,支付系统会去Redis缓存中查询是否存在该订单号的Key,如果不存在,则向Redis增加Key为订单号。查询订单支付已经支付,如果没有则进行支付,支付完成后删除该订单号的Key。通过Redis做到了分布式锁,只有这次订单订单支付请求完成,下次请求才能进来。 相比去重表,将放并发做到了缓存中,较为高效。思路相同,同一时间只能完成一次支付请求。
token令牌
这种方式分成两个阶段:申请token阶段和支付阶段。 第一阶段,在进入到提交订单页面之前,需要订单系统根据用户信息向支付系统发起一次申请token的请求,支付系统将token保存到Redis缓存中,为第二阶段支付使用。 第二阶段,订单系统拿着申请到的token发起支付请求,支付系统会检查Redis中是否存在该token,如果存在,表示第一次发起支付请求,删除缓存中token后开始支付逻辑处理;如果缓存中不存在,表示非法请求。 实际上这里的token是一个信物,支付系统根据token确认,你是你妈的孩子。 不足是需要系统间交互两次,流程较上述方法复杂。
支付缓冲区
把订单的支付请求都快速地接下来,一个快速接单的缓冲管道。后续使用异步任务处理管道中的数据,过滤掉重复的待支付订单。 优点是同步转异步,高吞吐。不足是不能及时地返回支付结果,需要后续监听支付结果的异步返回。