Python数据分析难？手把手教你处理上万条京东订单数据（附源码）

数据集简介

本数据集共收集了发生在一个月内的28010条数据，包含以下字段：

• ['订单编号', '总金额', '买家实际支付金额', '收货地址', '订单创建时间', '订单付款时间 ', '退款金额']

7个字段说明：

• 订单编号：订单编号;
• 总金额：订单总金额;
• 买家实际支付金额：总金额 - 退款金额(在已付款的情况下)。金额为0(在未付款的情况下);
• 收货地址：各个省份;
• 订单创建时间：下单时间;
• 订单付款时间：付款时间;
• 退款金额：付款后申请退款的金额。如无付过款，退款金额为0。

数据概览： 

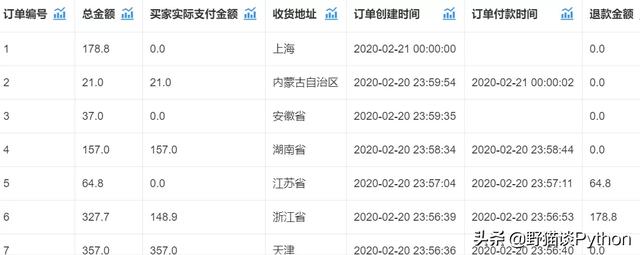
相关库、函数和数据的导入

# 相关库和函数的导入 
 
import numpy as np 
from sklearn import metrics 
import math 
import copy 
import pandas as pd           
import scipy as sp导入常用的基本库 
 
import datetime as date                                 # 导入datetime库 
import seaborn as sns                                   # 导入seaborn库，用于数据可视化 
from IPython.display import display                     # 载入数据查看时需要使用的函数 
from sklearn.model_selection import train_test_split    # 导入数据集划分时需要使用的函数 
from sklearn.metrics import confusion_matrix            # 导入生成混淆矩阵的函数 
from sklearn.preprocessing import LabelEncoder          # 导入分类变量编码时需要使用的函数 
from sklearn.metrics import classification_report       # 导入分类结果评价时要用到的函数 
 
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis     # 导入LDA判别时需要使用的函数 
from sklearn.naive_bayes import MultinomialNB           # 导入朴素贝叶斯时需要使用的额函数 
from sklearn.neighbors import KNeighborsClassifier      # 导入KNN判别时需要使用的函数 
from sklearn.tree import DecisionTreeClassifier         # 导入决策树函数 
from sklearn.neural_network import MLPClassifier        # 导入神经网络函数 
from sklearn import svm                                 # 导入支持向量机函数 
 
from sklearn.model_selection import GridSearchCV        # 导入模型优化方法中的网格搜索法需要用到的函数 
from sklearn.cross_validation import KFold              # 导入模型评估时使用的函数 
 
# 数据导入 
 
dt = pd.read_csv('D:资料/数据分析/数据分析与数据挖掘/实战演练/5（tmall_order_report）/tmall_order_report.csv',encoding='gbk',engine='python') 

数据检查与清洗

首先，查看一下数据集的变量类型：

dt.dtypes                                               # 查看数据集有哪些变量  

然后，将变量中右侧的空格去除(以免影响后续调用变量)，并进行重复值和缺失值检查：

dt.columns = dt.columns.str.rstrip()                    # 去除列名右侧的空格 
dt.duplicated().sum()                                   # 检查数据是否有重复值，发现并没有重复值 
display(sum(dt.isnull().sum()))                         # 检查数据集是否有缺失值  

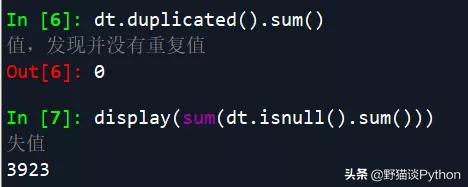
检查出来有缺失值(约占数据总量的12-15%)，考虑原数据中是否是因为“订单付款时间”这一列存在缺失值而导致产生这样的检查结果：

col = dt.columns.values.tolist()                        # 提取数据集中的所有列变量的名称 
col.remove('订单付款时间')                               # 将订单付款时间这一列去除 
display(sum(dt[col].isnull().sum()))                    # 再次检查是否有缺失值，发现并没有缺失值，也就是缺失值均来自“订单付款时间”这一列  

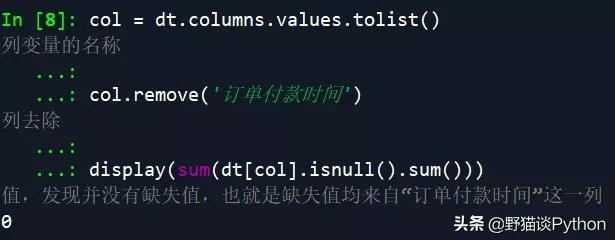
结果表明，缺失值仅来自“订单付款时间”这一列。接下来就是处理缺失值，处理的思路可以是先计算出各订单付款时间和下单时间的平均值，然后用下单时间 + 平均值，作为缺失值的填补对象：

c = np.array(['订单创建时间','订单付款时间'])             # 提取订单创建时间、付款时间这两列的列名 
for i in c: 
    dt[i] = pd.to_datetime(dt[i])                       # 将订单创建时间、付款时间由object类型转为datetime类型，方便运算 
for i in range(0,dt.shape[0]): 
    if (dt['订单付款时间'].iloc[i] < dt['订单创建时间'].iloc[i]) == True: 
        dt['订单付款时间'].iloc[i] = dt['订单付款时间'].iloc[i] + date.timedelta(days=1)     # 将订单付款时间 < 订单创建时间的时间数据往后加1天（因为原数据中没有考虑日期差异情况)  
mu = np.mean(dt['订单付款时间']-dt['订单创建时间'])       # 计算时间差的均值，用于之后进行缺失值替换 
for i in range(0,dt.shape[0]): 
    if pd.isnull(dt['订单付款时间'].iloc[i]) == True:    # 进行缺失值填补 
        dt['订单付款时间'].iloc[i] = dt['订单创建时间'].iloc[i] + mu 

在填补完成之后，再次检查缺失值和重复值的情况：

display(sum(dt.isnull().sum()))                         # 再次检查数据集是否有缺失值，发现已经处理完了，但是还要检查是否增加正确 
display(dt.duplicated().sum())                          # 再次检查数据是否有重复值，发现并没有重复值，发现也没有重复值 

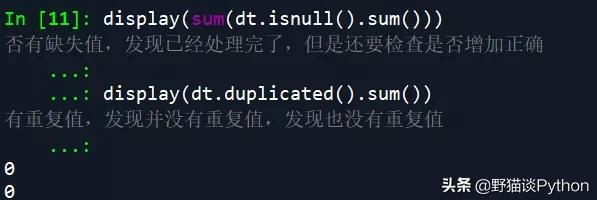
结果显示已经没有缺失值和重复值了。

描述性分析

首先，对订单总金额进行描述性分析：

display(dt['总金额'].describe())                        # 查看订单总金额的情况，发现最大的订单价格达到了188320元，最小的则只有1元，平均订单价为107元左右  

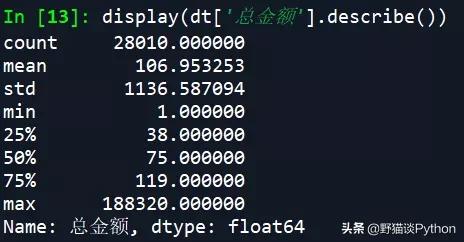
从描述统计的结果中可以看到，最大的订单价格达到了188320元，最小的只有1元，平均订单价在107元左右，中位数为1元，说明应该是一个左偏分布，即大部分订单的价格应该都不高。然后查看买家实际支付金额为0(支付未完成)的订单比例：

sum(dt['买家实际支付金额']==0) / dt.shape[0]             # 查看买家实际支付金额为0（也就是支付未完成）的订单比例，占比约为32.3%  

从结果中可以看到，大概有32.3%的买家未完成支付，这一比例还是比较高的。再看看订单付款时间相比于订单创建时间的延迟情况：

display((dt['订单付款时间']-dt['订单创建时间']).describe())     # 查看订单付款时间相比于订单创建时间的延迟情况，发现最慢的支付延迟了接近1天，而大部分订单在10分钟内就完成了支付 

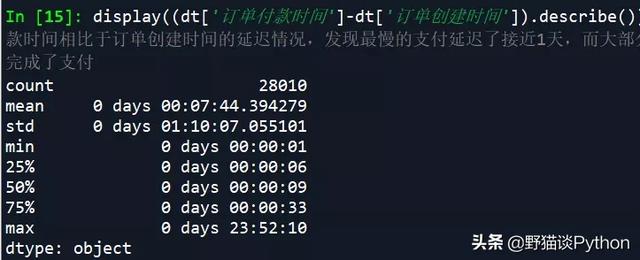
从中可以看到，最慢的支付延迟了接近1天，而大部分订单在10分钟内就完成了支付。最后，来对收货地址情况进行描述性分析：

siz = dt.groupby(dt['收货地址']).size()                 # 对收货地址进行分组统计 
idx_sort = np.argsort(-siz)                            # 对分组统计的结果进行降序排序 
display(siz[idx_sort].head())                          # 查看降序排序的结果的前5名，发现收货地址选择上海、广东、江苏、浙江、北京的最多 
siz[idx_sort].tail()                                   # 查看降序排序的结果的最后5名，发现收货地址选择湖北、新疆、宁夏、青海和西藏的最少，其中湖北可能受疫情影响所致 

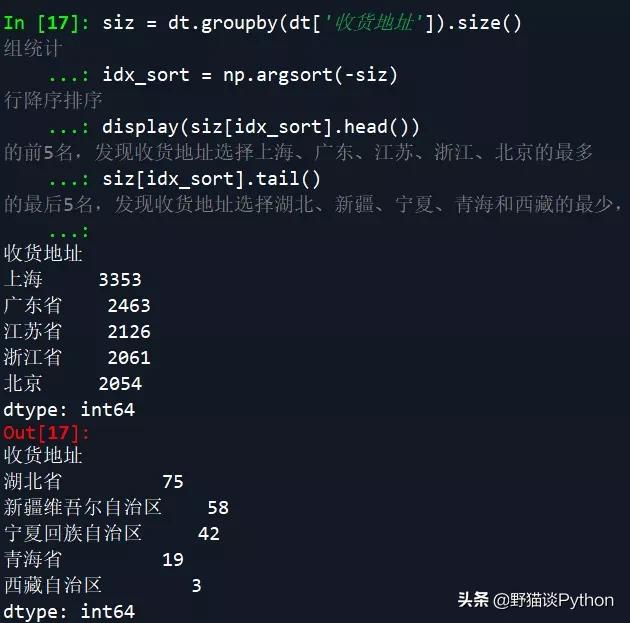
从结果中可以看到，收货地址选择上海、广东、江苏、浙江、北京的最多，而选湖北、新疆、宁夏、青海和西藏的最少，其中湖北可能受疫情影响所致。

建模预处理

首先，进行特征构建，并生成用于建模的数据集，处理过程如下：

d1 = (dt['订单付款时间']-dt['订单创建时间'])            # 输出订单付款和创建之间的时间差，作为一个新变量 
d1 = (d1 / np.timedelta64(1, 's')).astype(int)        # 将时间差的格式进行转换，转换为按秒计数，并把格式变为int类型 
le_train = LabelEncoder()                             # 使用从sklearn.preprocessing中import的LabelEncoder对分类数据进行编码，以便于后续使用交叉验证建模  
le_train.fit(dt['收货地址'].tolist())                  # 对模型进行训练 
d2 = le_train.transform(dt['收货地址'].tolist())       # 转化数据，作为第2个变量 
d3 = np.zeros(dt.shape[0])                            # 构建一个全为0的数组 
for i in range(0,dt.shape[0]): 
    if (dt['总金额'].iloc[i]-dt['买家实际支付金额'].iloc[i]) == dt['退款金额'].iloc[i]: 
        d3[i] = 1                                     # 生成一个新变量(类别变量)，当买家有支付（无论退不退款）时为1，没有支付时为0（无支付时上述等式不成立，实际支付金额和退款金额均为0），表明支付的情况 
dt_use = np.vstack((d1,d2,d3)).T                      # 生成用于建模分析的数据集，np.vstack用于数组的垂直连接   

然后是对数据集进行划分，形成训练集和测试集，为之后的建模做准备：

x_train,x_test, y_train, y_test = train_test_split(dt_use[:,0:2],dt_use[:,2:3],test_size=0.25, random_state=0)     # 使用从sklearn.model_selection中import的train_test_split函数进行训练集、测试集的划分 
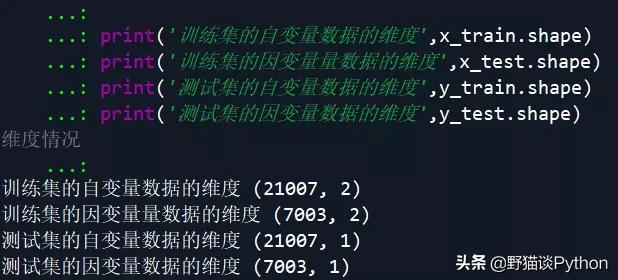
print('训练集的自变量数据的维度',x_train.shape) 
print('训练集的因变量量数据的维度',x_test.shape) 
print('测试集的自变量数据的维度',y_train.shape)           
print('测试集的因变量数据的维度',y_test.shape)          # 查看数据集划分后的维度情况  

数据建模

首先，构建初始的模型，这里完成的是分类预测任务，选择经典的几个模型，分别是 SVM、LDA、朴素贝叶斯NB、KNN判别、决策树Detree和神经网络Network：

models = {}                                           # 构建一个models集合 
models['SVM'] = svm.SVC()                             # 支持向量机模型 
models['LDA'] = LinearDiscriminantAnalysis()          # LDA判别模型 
models['NB'] = MultinomialNB()                        # 朴素贝叶斯模型 
models['KNN'] = KNeighborsClassifier()                # KNN判别模型 
models['Detree'] = DecisionTreeClassifier()           # 决策树模型 
models['Network'] = MLPClassifier()                   # 神经网络模型 

然后，对模型进行训练和分析：

target_names = ['有支付','没有支付']                   # 生成类别的名称 
for key in models: 
    models[key].fit(x_train,y_train)                  # 模型训练 
    display(confusion_matrix(y_test,models[key].predict(x_test)))                                               # 对y_test进行预测，输出混淆矩阵 
    print(classification_report(y_test,models[key].predict(x_test),target_names=target_names))                  # 对y_test进行预测，输出预测的分类评价 
    print('\n')    

SVM模型的混淆矩阵和准确率： 

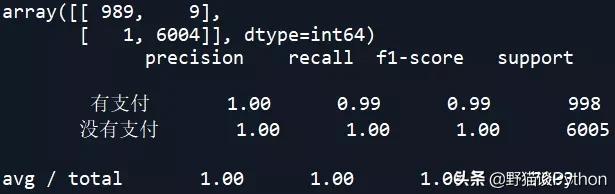
LDA模型的混淆矩阵和准确率： 

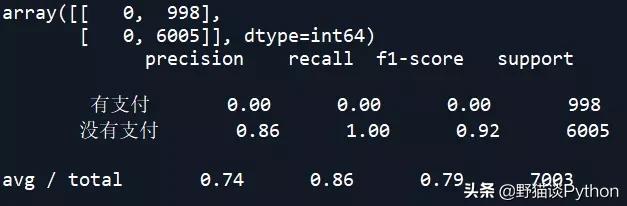
朴素贝叶斯NB模型的混淆矩阵和准确率： 

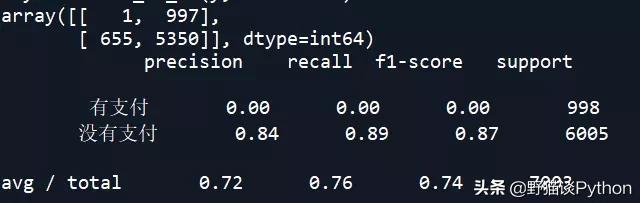
KNN判别模型的混淆矩阵和准确率： 

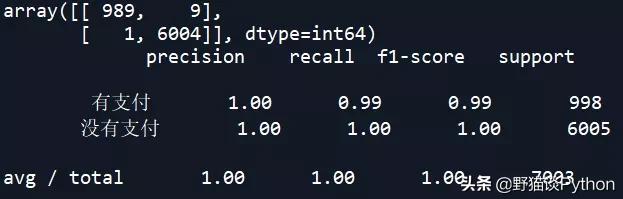
决策树Detree模型的混淆矩阵和准确率： 

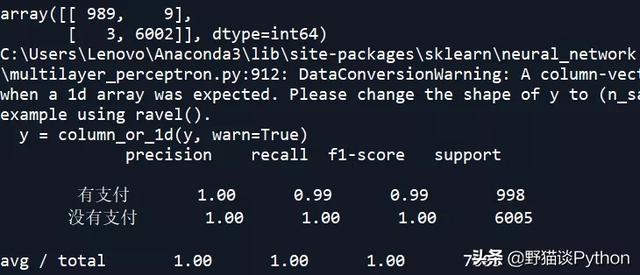
神经网络Network模型的混淆矩阵和准确率： 

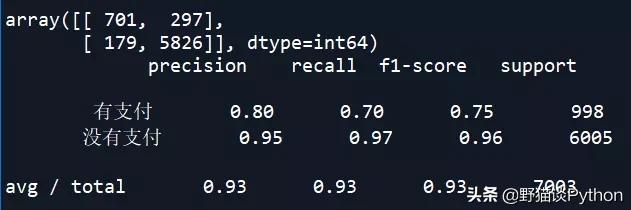
从上述结果中可以看到，SVM和KNN的准确率较高。下面对朴素贝叶斯NB模型进行调参，看是否能改善其预测准确率：

param_grid_nb = {'alpha':[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]}    # 设定贝叶斯模型中不同alpha值 
model_nb_ty = MultinomialNB()                          # 设定贝叶斯的模型 
kfold = KFold(10, 6)                                   # 采用10折交叉验证，初始随机起点为6 
grid = GridSearchCV(estimator=model_nb_ty,  
                    param_grid=param_grid_nb, scoring='neg_mean_squared_error', cv=kfold)         # 设置网格搜索的模型 
grid_result = grid.fit(x_train, y_train)               # 利用构建好的模型对数据集进行训练，搜索最优的k值 
print('最优：%s 使用%s' % (grid_result.best_score_, grid_result.best_params_))                     # 输出最优的参数情况 
nb_model = MultinomialNB(alpha=0)                      # 根据模型调参的结果，重新设定朴素贝叶斯模型 
nb_model.fit(x_train,y_train)                          # 模型训练 
display(confusion_matrix(y_test,nb_model.predict(x_test)))                                        # 对y_test进行预测，输出混淆矩阵 
print(classification_report(y_test,nb_model.predict(x_test),target_names=target_names))           # 对y_test进行预测，输出预测的分类评价，发现并没有什么改进  

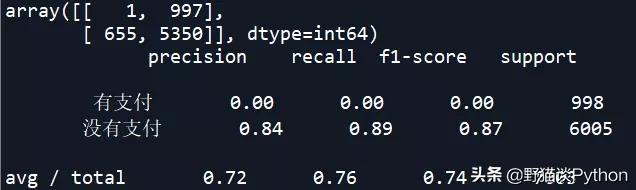
调参后的结果和调参前并没有多少改善，说明NB模型在本次预测中受限于数据情况，而不是模型参数。

最后放上全过程的代码，供大家学习使用：

### 数据分析前期准备工作 ### 
 
# 相关库和函数的导入 
 
import numpy as np 
from sklearn import metrics 
import math 
import copy 
import pandas as pd           
import scipy as sp 
import matplotlib.pyplot as plt               # 导入常用的基本库 
 
import datetime as date                                 # 导入datetime库 
import seaborn as sns                                   # 导入seaborn库，用于数据可视化 
from IPython.display import display                     # 载入数据查看时需要使用的函数 
from sklearn.model_selection import train_test_split    # 导入数据集划分时需要使用的函数 
from sklearn.metrics import confusion_matrix            # 导入生成混淆矩阵的函数 
from sklearn.preprocessing import LabelEncoder          # 导入分类变量编码时需要使用的函数 
from sklearn.metrics import classification_report       # 导入分类结果评价时要用到的函数   
 
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis     # 导入LDA判别时需要使用的函数 
from sklearn.naive_bayes import MultinomialNB           # 导入朴素贝叶斯时需要使用的额函数 
from sklearn.neighbors import KNeighborsClassifier      # 导入KNN判别时需要使用的函数 
from sklearn.tree import DecisionTreeClassifier         # 导入决策树函数 
from sklearn.neural_network import MLPClassifier        # 导入神经网络函数 
from sklearn import svm                                 # 导入支持向量机函数 
 
from sklearn.model_selection import GridSearchCV        # 导入模型优化方法中的网格搜索法需要用到的函数 
from sklearn.cross_validation import KFold              # 导入模型评估时使用的函数 
 
# 全局设定 
 
plt.rcParams['font.sans-serif']=['SimHei']              # 设定中文字符的显示设定 
 
# 数据导入 
 
dt = pd.read_csv('D:资料/数据分析/数据分析与数据挖掘/实战演练/5（tmall_order_report）/tmall_order_report.csv',encoding='gbk',engine='python') 
 
 
 
### 数据整理与查看 ### 
 
# 数据检查与清洗 
 
dt.dtypes                                               # 查看数据集有哪些变量 
 
dt.columns = dt.columns.str.rstrip()                    # 去除列名右侧的空格 
 
dt.duplicated().sum()                                   # 检查数据是否有重复值，发现并没有重复值 
 
display(sum(dt.isnull().sum()))                         # 检查数据集是否有缺失值 
 
col = dt.columns.values.tolist()                        # 提取数据集中的所有列变量的名称 
 
col.remove('订单付款时间')                               # 将订单付款时间这一列去除 
 
display(sum(dt[col].isnull().sum()))                    # 再次检查是否有缺失值，发现并没有缺失值，也就是缺失值均来自“订单付款时间”这一列 
 
c = np.array(['订单创建时间','订单付款时间'])             # 提取订单创建时间、付款时间这两列的列名 
 
for i in c: 
    dt[i] = pd.to_datetime(dt[i])                       # 将订单创建时间、付款时间由object类型转为datetime类型，方便运算 
 
for i in range(0,dt.shape[0]): 
    if (dt['订单付款时间'].iloc[i] < dt['订单创建时间'].iloc[i]) == True: 
        dt['订单付款时间'].iloc[i] = dt['订单付款时间'].iloc[i] + date.timedelta(days=1)     # 将订单付款时间 < 订单创建时间的时间数据往后加1天（因为原数据中没有考虑日期差异情况)  
 
mu = np.mean(dt['订单付款时间']-dt['订单创建时间'])       # 计算时间差的均值，用于之后进行缺失值替换 
 
for i in range(0,dt.shape[0]): 
    if pd.isnull(dt['订单付款时间'].iloc[i]) == True:    # 进行缺失值填补 
        dt['订单付款时间'].iloc[i] = dt['订单创建时间'].iloc[i] + mu 
 
display(sum(dt.isnull().sum()))                         # 再次检查数据集是否有缺失值，发现已经处理完了，但是还要检查是否增加正确 
 
display(dt.duplicated().sum())                          # 再次检查数据是否有重复值，发现并没有重复值，发现也没有重复值 
 
# 描述性分析 
 
display(dt['总金额'].describe())                        # 查看订单总金额的情况，发现最大的订单价格达到了188320元，最小的则只有1元，平均订单价为107元左右 
 
sum(dt['买家实际支付金额']==0) / dt.shape[0]             # 查看买家实际支付金额为0（也就是支付未完成）的订单比例，占比约为32.3% 
 
display((dt['订单付款时间']-dt['订单创建时间']).describe())     # 查看订单付款时间相比于订单创建时间的延迟情况，发现最慢的支付延迟了接近1天，而大部分订单在10分钟内就完成了支付 
 
siz = dt.groupby(dt['收货地址']).size()                 # 对收货地址进行分组统计 
idx_sort = np.argsort(-siz)                            # 对分组统计的结果进行降序排序 
display(siz[idx_sort].head())                          # 查看降序排序的结果的前5名，发现收货地址选择上海、广东、江苏、浙江、北京的最多 
siz[idx_sort].tail()                                   # 查看降序排序的结果的最后5名，发现收货地址选择湖北、新疆、宁夏、青海和西藏的最少，其中湖北可能受疫情影响所致 
 
 
 
### 建模预处理 ### 
 
# 特征构建 
 
d1 = (dt['订单付款时间']-dt['订单创建时间'])            # 输出订单付款和创建之间的时间差，作为一个新变量 
d1 = (d1 / np.timedelta64(1, 's')).astype(int)        # 将时间差的格式进行转换，转换为按秒计数，并把格式变为int类型 
 
le_train = LabelEncoder()                             # 使用从sklearn.preprocessing中import的LabelEncoder对分类数据进行编码，以便于后续使用交叉验证建模  
le_train.fit(dt['收货地址'].tolist())                  # 对模型进行训练 
d2 = le_train.transform(dt['收货地址'].tolist())       # 转化数据，作为第2个变量 
 
d3 = np.zeros(dt.shape[0])                            # 构建一个全为0的数组 
 
for i in range(0,dt.shape[0]): 
    if (dt['总金额'].iloc[i]-dt['买家实际支付金额'].iloc[i]) == dt['退款金额'].iloc[i]: 
        d3[i] = 1                                     # 生成一个新变量(类别变量)，当买家有支付（无论退不退款）时为1，没有支付时为0（无支付时上述等式不成立，实际支付金额和退款金额均为0），表明支付的情况 
 
dt_use = np.vstack((d1,d2,d3)).T                      # 生成用于建模分析的数据集，np.vstack用于数组的垂直连接    
 
# 数据集划分 
 
x_train,x_test, y_train, y_test = train_test_split(dt_use[:,0:2],dt_use[:,2:3],test_size=0.25, random_state=0)     # 使用从sklearn.model_selection中import的train_test_split函数进行训练集、测试集的划分 
 
print('训练集的自变量数据的维度',x_train.shape) 
print('训练集的因变量量数据的维度',x_test.shape) 
print('测试集的自变量数据的维度',y_train.shape)           
print('测试集的因变量数据的维度',y_test.shape)          # 查看数据集划分后的维度情况 
 
 
 
### 数据建模 ### 
 
# 初始模型构建 
 
models = {}                                           # 构建一个models集合 
 
models['SVM'] = svm.SVC()                             # 支持向量机模型 
 
models['LDA'] = LinearDiscriminantAnalysis()          # LDA判别模型 
 
models['NB'] = MultinomialNB()                        # 朴素贝叶斯模型 
 
models['KNN'] = KNeighborsClassifier()                # KNN判别模型 
 
models['Detree'] = DecisionTreeClassifier()           # 决策树模型 
 
models['Network'] = MLPClassifier()                   # 神经网络模型 
 
# 模型训练与分析 
 
target_names = ['有支付','没有支付']                   # 生成类别的名称 
 
for key in models: 
    models[key].fit(x_train,y_train)                  # 模型训练 
    display(confusion_matrix(y_test,models[key].predict(x_test)))                                               # 对y_test进行预测，输出混淆矩阵 
    print(classification_report(y_test,models[key].predict(x_test),target_names=target_names))                  # 对y_test进行预测，输出预测的分类评价 
    print('\n') 
     
# 模型调参（NB模型） 
 
param_grid_nb = {'alpha':[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]}    # 设定贝叶斯模型中不同alpha值 
 
model_nb_ty = MultinomialNB()                          # 设定贝叶斯的模型 
 
kfold = KFold(10, 6)                                   # 采用10折交叉验证，初始随机起点为6 
 
grid = GridSearchCV(estimator=model_nb_ty,  
                    param_grid=param_grid_nb, scoring='neg_mean_squared_error', cv=kfold)         # 设置网格搜索的模型 
 
grid_result = grid.fit(x_train, y_train)               # 利用构建好的模型对数据集进行训练，搜索最优的k值 
 
print('最优：%s 使用%s' % (grid_result.best_score_, grid_result.best_params_))                     # 输出最优的参数情况 
 
nb_model = MultinomialNB(alpha=0)                      # 根据模型调参的结果，重新设定朴素贝叶斯模型 
 
nb_model.fit(x_train,y_train)                          # 模型训练 
 
display(confusion_matrix(y_test,nb_model.predict(x_test)))                                        # 对y_test进行预测，输出混淆矩阵 
 
print(classification_report(y_test,nb_model.predict(x_test),target_names=target_names))           # 对y_test进行预测，输出预测的分类评价，发现并没有什么改进