介绍
假设您已经建立了一个面部识别模型,并且现在使用验证集来调整测试集上的实验参数。 可悲的是,您的实验得出的测试结果令人失望。
我们如何知道针对此特定问题的优秀的补救方法是什么?
首先了解假设提升问题,然后看看是否可以从衍生自该算法的AdaBoost算法的结果中提取实用原理,从而解决该问题。
线性预测器
线性回归
线性回归建模解释变量或自变量与标量响应或因变量之间的关系。
使用线性预测函数对关系进行建模。
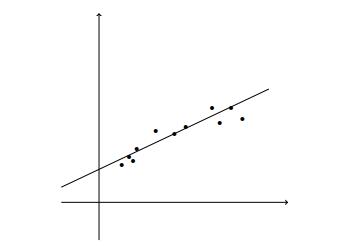
> Linear Regression
回归的损失函数需要定义由于我们的预测与标签或目标的真实结果之间的差异而应受到的惩罚。
均方误差使用平方损失函数来最小化此差异。
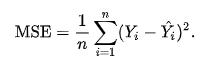
> Mean Squared Error
其中n是预测数,Y是被预测变量的观测值,而Ŷ是预测值。
一些学习任务需要非线性预测器,例如多项式预测器。
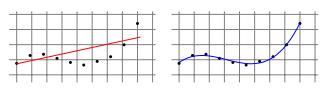
> Linear Regression for Polynomial Regression Tasks
通过使用最小二乘算法找到系数的优秀矢量,可以将这个问题简化为线性回归问题,该算法最小化了曲线上各点的偏移的平方和("残差")。
逻辑回归
在逻辑回归中,我们学习对间隔[0,1]上存在的某个类别或事件的概率进行建模。
逻辑函数是一个S型函数,它接受任何实际输入,并输出一个介于0和1之间的值。
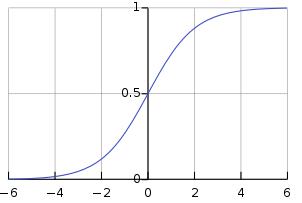
> Sigmoid function
如果此处的学习失败,我们可以尝试增强以解决偏差-偏差权衡问题。
假设提振问题
"一组弱学习者可以创造一个单一的强学习者吗?" —迈克尔·科恩斯(Michael Kerns)和莱斯利·加布里埃尔·莱斯(Leslie Gabriel Valiant)
Boosting使用线性预测变量的泛化来解决以下问题:
偏差-方差权衡
让我们定义一些术语:
- 近似误差是我们先验知识的误差,或者是我们的算法以何种概率输出最佳答案。
- 估计误差是我们的算法将预测看不见数据的结果的误差。
候选模型越复杂,近似误差越小,但是估计误差越大。
通过使学习者从可能具有较大近似误差的简单模型开始,发展为使近似误差和估计误差均最小的模型,Boosting使学习者可以控制此折衷。
学习的计算复杂性
提升可以提高弱势学习者或简单算法的准确性,而简单算法的性能要比随机猜测好一点。 这个想法是试图将弱学习者转变为强学习者,以便产生一个与难以学习和计算复杂的学习者相当的高效预测器。
自适应提升
AdaBoost(自适应增强)是一种基于理论假设增强问题的算法,该算法将假设的线性组合与检测图像中人脸的单个假设组成。
AdaBoost的伪代码,

> AdaBoost pseudocode
对于指定的回合数,AdaBoost算法分配权重,该权重与每个假设的误差成反比。 然后在假设正确的情况下更新此权重,这将获得较低的概率权重,而与假设不正确的示例相反。 这是针对多个回合执行的,因此,在每个后续回合中,弱学习者会将注意力集中在有问题的样本上。 然后,这会基于所有弱假设的加权总和产生一个"强分类器"。
其中T是训练回合的数量,h是弱学习者的运行时间,AdaBoost算法的运行时间有效地为O(Th)。
AdaBoost用于人脸识别
让我们回到我们的示例,在此示例中,我们要构建一个人脸识别模型,该模型采用24 x 24像素的图像并使用该信息来确定图像是否描绘了人脸。
我们将使用代表这四个基本假设的线性函数,
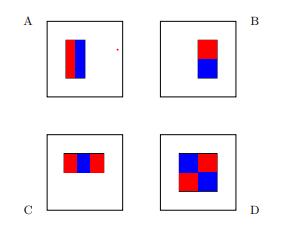
> Base hypotheses for face recognition
每个假设的功能形式包括:
- 轴对齐矩形R,最多24个轴对齐矩形
- A,B,C或D型
并将图像映射到标量值。
为了计算我们的学习函数,我们计算位于红色矩形内的像素的灰度值之和,然后从蓝色矩形内的像素的灰度值之和中减去该值。
我们可以通过首先在每个图像上计算函数的所有可能输出,然后应用AdaBoost算法来实现弱学习者。 这导致强度在脸部区域中增长,这可能导致更好的预测。
模型选择与验证
我们已经到了最终解决方案可以选择几种模型的地步。
解决我们特定问题的优秀模型是什么?
我们可以将样本划分为训练集和测试集,以便在近似误差和估计误差之间找到平衡。 在训练模型时,我们将使用训练集,并且将使用独立测试集来验证模型,以获取经验误差。 这将使我们有直觉来了解我们是过度拟合,过于紧密地拟合我们的训练样本,还是欠拟合而不充分地拟合我们的训练样本。
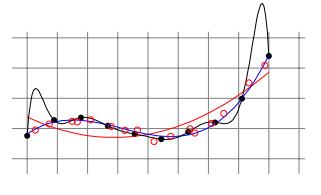
> Validation for model selection on polynomial regressors
近似误差和估计误差到底取决于什么?
首先定义一些术语:
- 让我们的假设类别代表我们可以为机器学习算法选择的所有可能假设的集合。
- 让我们将分布定义为未知函数,该函数确定从样本空间进行任何单独观察的真实概率。
我们的近似误差取决于分布和假设类别。 增加假设类别或使用其他特征表示可能会为我们提供一些替代知识,这些知识可能会改善近似误差。
我们的估计误差取决于训练样本量。 为了改善估计误差,我们必须有足够数量的训练样本。 较大的假设类别通常会增加估计误差,因为这会使找到良好的预测变量更加困难。 AdaBoost算法的结果是产生一个"强分类器",该分类器基于所有弱假设的加权和,从本质上减少了假设类别。
结论
从线性回归到自适应提升向我们展示了一个示例,说明如何解决学习成绩差的问题是模棱两可的。
模型选择,验证和学习曲线是我们可以用来帮助我们了解学习失败的原因以便找到补救措施的工具。
很好地总结了以下原则,这些原则直接来自对机器学习的理解:从理论到算法:
1.如果学习涉及参数调整,请绘制模型选择曲线以确保适当调整了参数。
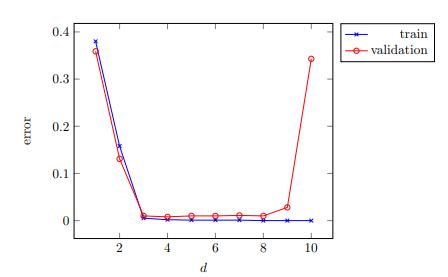
> Model-selection curve
2.如果训练误差过大,请考虑扩大假设类别,完全更改它,或更改数据的特征表示。
3.如果训练误差较小,则绘制学习曲线并尝试从中推断出问题是估计误差还是近似误差。
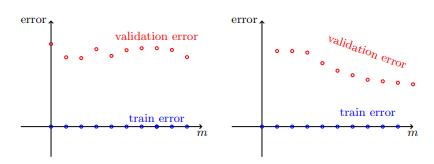
> Learning curves : estimation error vs approximation error
4.如果近似误差似乎足够小,请尝试获取更多数据。 如果这不可能,请考虑降低假设类别的复杂性。
5.如果近似误差似乎也很大,请尝试完全更改假设类别或数据的特征表示。




























