对于定量数据,要想了解其分布形式是对称的还是非对称的、发现某些特大或特小的可疑值,可做出频率分布表、绘制频率分布直方图、绘制茎叶图进行直观分析;对于定性数据,可用饼图和条形图直观地显示其分布情况。
01 定量数据的分布分析
对于定量变量而言,选择“组数”和“组宽”是做频率分布分析时最主要的问题,一般按照以下步骤进行:
- 第一步:求极差。
- 第二步:决定组距与组数。
- 第三步:决定分点。
- 第四步:列出频率分布表。
- 第五步:绘制频率分布直方图。
遵循的主要原则如下:
- 各组之间必须是相互排斥的。
- 各组必须将所有的数据包含在内。
- 各组的组宽最好相等。
下面结合具体实例来运用分布分析对定量数据进行特征分析。
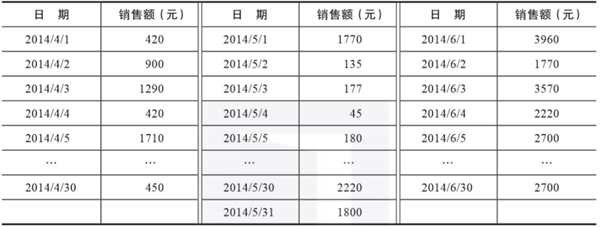
表3-2是菜品“捞起生鱼片”在2014年第二个季度的销售数据,绘制销售量的频率分布表、频率分布图,对该定量数据做出相应的分析。
▲表3-2 “捞起生鱼片”的销售情况
1. 求极差
极差=最大值-最小值=3960-45=3915
2. 分组
这里根据业务数据的含义,可取组距为500,则组数如下所示。
组数=极差/组距=3915/500=7.83≈8
3. 决定分点
分布区间如表3-3所示。
▲表3-3 分布区间
4. 绘制频率分布直方表
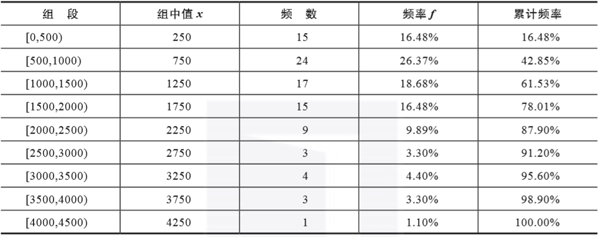
根据分组区间得到如表3-4所示的频率分布表。
- 其中,第1列将数据所在的范围分成若干组段,其中第1个组段要包括最小值,最后一个组段要包括最大值。习惯上将各组段设为左闭右开的半开区间,如第一个组段为[0,500)。
- 第2列组中值是各组段的代表值,由本组段的上限值和下限值相加除以2得到。
- 第3列和第4列分别为频数和频率。
- 第5列是累计频率,是否需要计算该列数值视情况而定。
▲表3-4 频率分布
5. 绘制频率分布直方图
若以2014年第二季度“捞起生鱼片”这道菜每天的销售额组段为横轴,以各组段的频率密度(频率与组距之比)为纵轴,表3-4中的数据可绘制成频率分布直方图,如代码清单3-3所示。
- 代码清单3-3 “捞起生鱼片”的季度销售情况
- import pandas as pd
- import numpy as np
- catering_sale = '../data/catering_fish_congee.xls' # 餐饮数据
- data = pd.read_excel(catering_sale,names=['date','sale']) # 读取数据,指定“日期”
- 列为索引
- bins = [0,500,1000,1500,2000,2500,3000,3500,4000]
- labels = ['[0,500)','[500,1000)','[1000,1500)','[1500,2000)',
- '[2000,2500)','[2500,3000)','[3000,3500)','[3500,4000)']
- data['sale分层'] = pd.cut(data.sale, bins, labelslabels=labels)
- aggResult = data.groupby(by=['sale分层'])['sale'].agg({'sale': np.size})
- pAggResult = round(aggResult/aggResult.sum(), 2, ) * 100
- import matplotlib.pyplot as plt
- plt.figure(figsize=(10,6)) # 设置图框大小尺寸
- pAggResult['sale'].plot(kind='bar',width=0.8,fontsize=10) # 绘制频率直方图
- plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
- plt.title('季度销售额频率分布直方图',fontsize=20)
- plt.show()
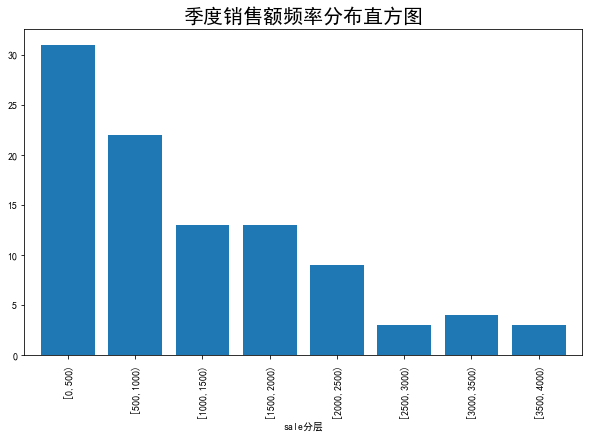
运行代码清单3-3可得季度销售额频率分布直方图,如图3-3所示。
▲图3-3 季度销售额频率分布直方图
02 定性数据的分布分析
对于定性变量,常常根据变量的分类类型来分组,可以采用饼图和条形图来描述定性变量的分布,如代码清单3-4所示。
- 代码清单3-4 不同菜品在某段时间的销售量分布情况
- import pandas as pd
- import matplotlib.pyplot as plt
- catering_dish_profit = '../data/catering_dish_profit.xls'# 餐饮数据
- data = pd.read_excel(catering_dish_profit) # 读取数据,指定“日期”列
- 为索引
- # 绘制饼图
- x = data['盈利']
- labels = data['菜品名']
- plt.figure(figsize=(8, 6)) # 设置画布大小
- plt.pie(x,labelslabels=labels) # 绘制饼图
- plt.rcParams['font.sans-serif'] = 'SimHei'
- plt.title('菜品销售量分布(饼图)') # 设置标题
- plt.axis('equal')
- plt.show()
- # 绘制条形图
- x = data['菜品名']
- y = data['盈利']
- plt.figure(figsize=(8, 4)) # 设置画布大小
- plt.bar(x,y)
- plt.rcParams['font.sans-serif'] = 'SimHei'
- plt.xlabel('菜品') # 设置x轴标题
- plt.ylabel('销量') # 设置y轴标题
- plt.title('菜品销售量分布(条形图)')# 设置标题
- plt.show() # 展示图片
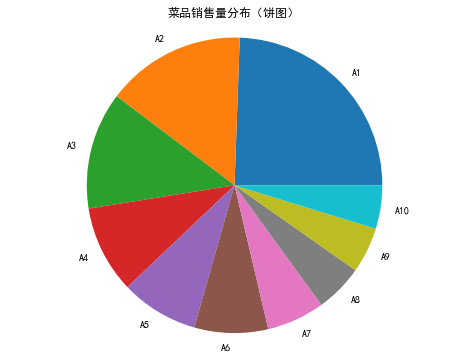
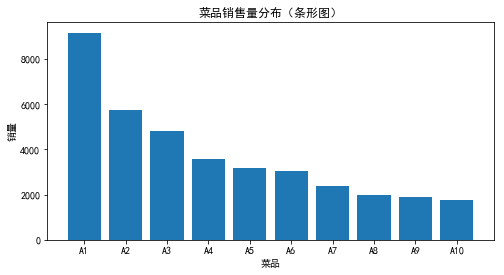
饼图的每一个扇形部分代表每一类型的所占百分比或频数,根据定性变量的类型数目将饼图分成几个部分,每一部分的大小与每一类型的频数成正比;条形图的高度代表每一类型的百分比或频数,条形图的宽度没有意义。
运行代码清单3-4可得不同菜品在某段时间的销售量分布图,如图3-4和图3-5所示。
▲图3‑4 菜品销售量分布(饼图)
▲图3‑5 菜品销售量分布(条形图)
关于作者:张良均,资深大数据挖掘与分析专家、模式识别专家、AI技术专家。有10余年大数据挖掘与分析经验,擅长Python、R、Hadoop、Matlab等技术实现的数据挖掘与分析,对机器学习等AI技术驱动的数据分析也有深入研究。
本文摘编自《Python数据分析与挖掘实战》(第2版),经出版方授权发布。