前言
最近刷力扣题,对于我这种 0 基础来说,真的是脑壳疼啊。这个月我估计都是中等和困难题,没有简单题了。
幸好,力扣上有各种大牛给写题解。看着他们行云流水的代码,真的是羡慕不已。让我印象最深刻的就是人称 “甜姨” 的知心姐姐,还有名叫威哥的大哥。几乎每天他们的题解我都是必看的。
甜姨的题解,虽然姿势很帅,但是对于我这种新手来说,感觉不是太友好,因为思路写的太少,不是很详细。所以,每次我看不明白的时候,都得反复看好几遍,才能想明白她代码中的思路。
上个周末的一道题是,让实现一个 LFU 缓存算法。经过我几个小时的研究(其实,应该有8个小时以上了,没得办法啊,菜就得多勤奋咯),终于把甜姨的思路整明白了。为了便于以后自己复习,就把整个思路记下来了,并配上图示和大量代码注释,我相信对于跟我一样的新手来说,是非常友好的。
经过甜姨同意,参考来源我也会贴出来:https://leetcode-cn.com/problems/lfu-cache/solution/java-13ms-shuang-100-shuang-xiang-lian-biao-duo-ji/
虽然,力扣要求是用时间复杂度 O(1) 来解,但是其它方式我感觉也有必要了解,毕竟是一个由浅到深的过程,自己实现一遍总归是好的。因此,我就把五种求解方式,从简单到复杂,都讲一遍。
LFU实现
力扣原题描述如下:
- 请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。它应该支持以下操作:get 和 put。
- get(key) - 如果键存在于缓存中,则获取键的值(总是正数),否则返回 -1。
- put(key, value) - 如果键不存在,请设置或插入值。当缓存达到其容量时,则应该在插入新项之前,使最不经常使用的项无效。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 最近 最少使用的键。
- 「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。
- 示例:
- LFUCache cache = new LFUCache( 2 /* capacity (缓存容量) */ );
- cache.put(1, 1);
- cache.put(2, 2);
- cache.get(1); // 返回 1
- cache.put(3, 3); // 去除 key 2
- cache.get(2); // 返回 -1 (未找到key 2)
- cache.get(3); // 返回 3
- cache.put(4, 4); // 去除 key 1
- cache.get(1); // 返回 -1 (未找到 key 1)
- cache.get(3); // 返回 3
- cache.get(4); // 返回 4
- 来源:力扣(LeetCode)
- 链接:https://leetcode-cn.com/problems/lfu-cache
就是要求我们设计一个 LFU 算法,根据访问次数(访问频次)大小来判断应该删除哪个元素,get和put操作都会增加访问频次。当访问频次相等时,就判断哪个元素是最久未使用过的,把它删除。
因此,这道题需要考虑两个方面,一个是访问频次,一个是访问时间的先后顺序。
方案一:使用优先队列思路:
我们可以使用JDK提供的优先队列 PriorityQueue 来实现 。因为优先队列内部维护了一个二叉堆,即可以保证每次 poll 元素的时候,都可以根据我们的要求,取出当前所有元素的最大值或是最小值。只需要我们的实体类实现 Comparable 接口就可以了。
因此,我们需要定义一个 Node 来保存当前元素的访问频次 freq,全局的自增的 index,用于比较大小。然后定义一个 Map
当 cache 容量不足时,根据访问频次 freq 的大小来删除最小的 freq 。若相等,则删除 index 最小的,因为index是自增的,越大说明越是最近访问过的,越小说明越是很长时间没访问过的元素。
因本质是用二叉堆实现,故时间复杂度为O(logn)。
- public class LFUCache4 {
- public static void main(String[] args) {
- LFUCache4 cache = new LFUCache4(2);
- cache.put(1, 1);
- cache.put(2, 2);
- // 返回 1
- System.out.println(cache.get(1));
- cache.put(3, 3); // 去除 key 2
- // 返回 -1 (未找到key 2)
- System.out.println(cache.get(2));
- // 返回 3
- System.out.println(cache.get(3));
- cache.put(4, 4); // 去除 key 1
- // 返回 -1 (未找到 key 1)
- System.out.println(cache.get(1));
- // 返回 3
- System.out.println(cache.get(3));
- // 返回 4
- System.out.println(cache.get(4));
- }
- //缓存了所有元素的node
- Map<Integer,Node> cache;
- //优先队列
- Queue<Node> queue;
- //缓存cache 的容量
- int capacity;
- //当前缓存的元素个数
- int size;
- //全局自增
- int index = 0;
- //初始化
- public LFUCache4(int capacity){
- this.capacity = capacity;
- if(capacity > 0){
- queue = new PriorityQueue<>(capacity);
- }
- cache = new HashMap<>();
- }
- public int get(int key){
- Node node = cache.get(key);
- // node不存在,则返回 -1
- if(node == null) return -1;
- //每访问一次,频次和全局index都自增 1
- node.freq++;
- node.index = index++;
- // 每次都重新remove,再offer是为了让优先队列能够对当前Node重排序
- //不然的话,比较的 freq 和 index 就是不准确的
- queue.remove(node);
- queue.offer(node);
- return node.value;
- }
- public void put(int key, int value){
- //容量0,则直接返回
- if(capacity == 0) return;
- Node node = cache.get(key);
- //如果node存在,则更新它的value值
- if(node != null){
- node.value = value;
- node.freq++;
- node.index = index++;
- queue.remove(node);
- queue.offer(node);
- }else {
- //如果cache满了,则从优先队列中取出一个元素,这个元素一定是频次最小,最久未访问过的元素
- if(size == capacity){
- cache.remove(queue.poll().key);
- //取出元素后,size减 1
- size--;
- }
- //否则,说明可以添加元素,于是创建一个新的node,添加到优先队列中
- Node newNode = new Node(key, value, index++);
- queue.offer(newNode);
- cache.put(key,newNode);
- //同时,size加 1
- size++;
- }
- }
- //必须实现 Comparable 接口才可用于排序
- private class Node implements Comparable<Node>{
- int key;
- int value;
- int freq = 1;
- int index;
- public Node(){
- }
- public Node(int key, int value, int index){
- this.key = key;
- this.value = value;
- this.index = index;
- }
- @Override
- public int compareTo(Node o) {
- //优先比较频次 freq,频次相同再比较index
- int minus = this.freq - o.freq;
- return minus == 0? this.index - o.index : minus;
- }
- }
- }
方案二:使用一条双向链表
思路:
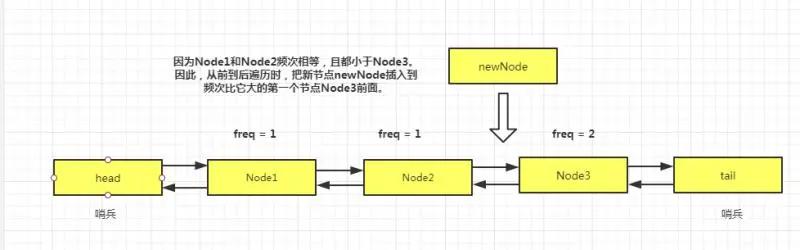
只用一条双向链表,来维护频次和时间先后顺序。那么,可以这样想。把频次 freq 小的放前面,频次大的放后面。如果频次相等,就从当前节点往后遍历,直到找到第一个频次比它大的元素,并插入到它前面。(当然,如果遍历到了tail,则插入到tail前面)这样可以保证同频次的元素,最近访问的总是在最后边。
因此,总的来说,最低频次,并且最久未访问的元素肯定就是链表中最前面的那一个了。这样的话,当 cache容量满的时候,直接把头结点删除掉就可以了。但是,我们这里为了方便链表的插入和删除操作,用了两个哨兵节点,来表示头节点 head和尾结点tail。因此,删除头结点就相当于删除 head.next。
PS:哨兵节点只是为了占位,实际并不存储有效数据,只是为了链表插入和删除时,不用再判断当前节点的位置。不然的话,若当前节点占据了头结点或尾结点的位置,还需要重新赋值头尾节点元素,较麻烦。
为了便于理解新节点如何插入到链表中合适的位置,作图如下:
代码如下:
- public class LFUCache {
- public static void main(String[] args) {
- LFUCache cache = new LFUCache(2);
- cache.put(1, 1);
- cache.put(2, 2);
- // 返回 1
- System.out.println(cache.get(1));
- cache.put(3, 3); // 去除 key 2
- // 返回 -1 (未找到key 2)
- System.out.println(cache.get(2));
- // 返回 3
- System.out.println(cache.get(3));
- cache.put(4, 4); // 去除 key 1
- // 返回 -1 (未找到 key 1)
- System.out.println(cache.get(1));
- // 返回 3
- System.out.println(cache.get(3));
- // 返回 4
- System.out.println(cache.get(4));
- }
- private Map<Integer,Node> cache;
- private Node head;
- private Node tail;
- private int capacity;
- private int size;
- public LFUCache(int capacity) {
- this.capacity = capacity;
- this.cache = new HashMap<>();
- /**
- * 初始化头结点和尾结点,并作为哨兵节点
- */
- head = new Node();
- tail = new Node();
- head.next = tail;
- tail.pre = head;
- }
- public int get(int key) {
- Node node = cache.get(key);
- if(node == null) return -1;
- node.freq++;
- moveToPostion(node);
- return node.value;
- }
- public void put(int key, int value) {
- if(capacity == 0) return;
- Node node = cache.get(key);
- if(node != null){
- node.value = value;
- node.freq++;
- moveToPostion(node);
- }else{
- //如果元素满了
- if(size == capacity){
- //直接移除最前面的元素,因为这个节点就是频次最小,且最久未访问的节点
- cache.remove(head.next.key);
- removeNode(head.next);
- size--;
- }
- Node newNode = new Node(key, value);
- //把新元素添加进来
- addNode(newNode);
- cache.put(key,newNode);
- size++;
- }
- }
- //只要当前 node 的频次大于等于它后边的节点,就一直向后找,
- // 直到找到第一个比当前node频次大的节点,或者tail节点,然后插入到它前面
- private void moveToPostion(Node node){
- Node nextNode = node.next;
- //先把当前元素删除
- removeNode(node);
- //遍历到符合要求的节点
- while (node.freq >= nextNode.freq && nextNode != tail){
- nextNode = nextNode.next;
- }
- //把当前元素插入到nextNode前面
- node.pre = nextNode.pre;
- node.next = nextNode;
- nextNode.pre.next = node;
- nextNode.pre = node;
- }
- //添加元素(头插法),并移动到合适的位置
- private void addNode(Node node){
- node.pre = head;
- node.next = head.next;
- head.next.pre = node;
- head.next = node;
- moveToPostion(node);
- }
- //移除元素
- private void removeNode(Node node){
- node.pre.next = node.next;
- node.next.pre = node.pre;
- }
- class Node {
- int key;
- int value;
- int freq = 1;
- //当前节点的前一个节点
- Node pre;
- //当前节点的后一个节点
- Node next;
- public Node(){
- }
- public Node(int key ,int value){
- this.key = key;
- this.value = value;
- }
- }
- }
可以看到不管是插入元素还是删除元素时,都不需要额外的判断,这就是设置哨兵节点的好处。
由于每次访问元素的时候,都需要按一定的规则把元素放置到合适的位置,因此,元素需要从前往后一直遍历。所以,时间复杂度 O(n)。
方案三:用 LinkedHashSet维护频次链表
思路:
我们不再使用一条链表,同时维护频次和访问时间了。此处,换为用 map 键值对来维护,用频次作为键,用当前频次对应的一条具有先后访问顺序的链表来作为值。它的结构如下:
- Map<Integer, LinkedHashSet<Node>> freqMap
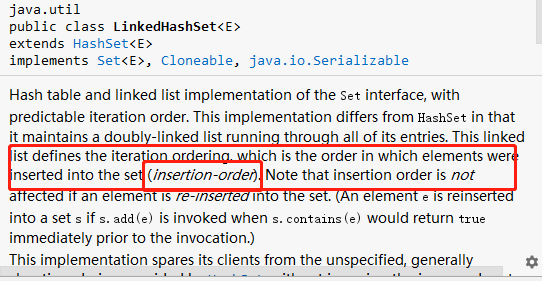
由于LinkedHashSet 的 iterator迭代方法是按插入顺序的,因此迭代到的第一个元素肯定是当前频次下,最久未访问的元素。这样的话,当缓存 cache满的时候,直接删除迭代到的第一个元素就可以了。
另外 freqMap,也需要在每次访问元素的时候,重新维护关系。从当前元素的频次对应的双向链表中移除当前元素,并加入到高频次的链表中。
- public class LFUCache1 {
- public static void main(String[] args) {
- LFUCache1 cache = new LFUCache1(2);
- cache.put(1, 1);
- cache.put(2, 2);
- // 返回 1
- System.out.println(cache.get(1));
- cache.put(3, 3); // 去除 key 2
- // 返回 -1 (未找到key 2)
- System.out.println(cache.get(2));
- // 返回 3
- System.out.println(cache.get(3));
- cache.put(4, 4); // 去除 key 1
- // 返回 -1 (未找到 key 1)
- System.out.println(cache.get(1));
- // 返回 3
- System.out.println(cache.get(3));
- // 返回 4
- System.out.println(cache.get(4));
- }
- //缓存 cache
- private Map<Integer,Node> cache;
- //存储频次和对应双向链表关系的map
- private Map<Integer, LinkedHashSet<Node>> freqMap;
- private int capacity;
- private int size;
- //存储最小频次值
- private int min;
- public LFUCache1(int capacity) {
- this.capacity = capacity;
- cache = new HashMap<>();
- freqMap = new HashMap<>();
- }
- public int get(int key) {
- Node node = cache.get(key);
- if(node == null) return -1;
- //若找到当前元素,则频次加1
- freqInc(node);
- return node.value;
- }
- public void put(int key, int value) {
- if(capacity == 0) return;
- Node node = cache.get(key);
- if(node != null){
- node.value = value;
- freqInc(node);
- }else{
- if(size == capacity){
- Node deadNode = removeNode();
- cache.remove(deadNode.key);
- size --;
- }
- Node newNode = new Node(key,value);
- cache.put(key,newNode);
- addNode(newNode);
- size++;
- }
- }
- //处理频次map
- private void freqInc(Node node){
- //从原来的频次对应的链表中删除当前node
- LinkedHashSet<Node> set = freqMap.get(node.freq);
- if(set != null)
- set.remove(node);
- //如果当前频次是最小频次,并且移除元素后,链表为空,则更新min值
- if(node.freq == min && set.size() == 0){
- min = node.freq + 1;
- }
- //添加到新的频次对应的链表
- node.freq ++;
- LinkedHashSet<Node> newSet = freqMap.get(node.freq);
- //如果高频次链表还未存在,则初始化一条
- if(newSet == null){
- newSet = new LinkedHashSet<Node>();
- freqMap.put(node.freq,newSet);
- }
- newSet.add(node);
- }
- //添加元素,更新频次
- private void addNode(Node node){
- //添加新元素,肯定是需要加入到频次为1的链表中的
- LinkedHashSet<Node> set = freqMap.get(1);
- if(set == null){
- set = new LinkedHashSet<>();
- freqMap.put(1,set);
- }
- set.add(node);
- //更新最小频次为1
- min = 1;
- }
- //删除频次最小,最久未访问的元素
- private Node removeNode(){
- //找到最小频次对应的 LinkedHashSet
- LinkedHashSet<Node> set = freqMap.get(min);
- //迭代到的第一个元素就是最久未访问的元素,移除之
- Node node = set.iterator().next();
- set.remove(node);
- //如果当前node的频次等于最小频次,并且移除元素之后,set为空,则 min 加1
- if(node.freq == min && set.size() == 0){
- min ++;
- }
- return node;
- }
- private class Node {
- int key;
- int value;
- int freq = 1;
- public Node(int key, int value){
- this.key = key;
- this.value = value;
- }
- public Node(){
- }
- }
- }
方案四:手动实现一个频次链表
思路:
由于方案三用的是JDK自带的 LinkedHashSet ,其是实现了哈希表和双向链表的一个类,因此为了减少哈希相关的计算,提高效率,我们自己实现一条双向链表来替代它。
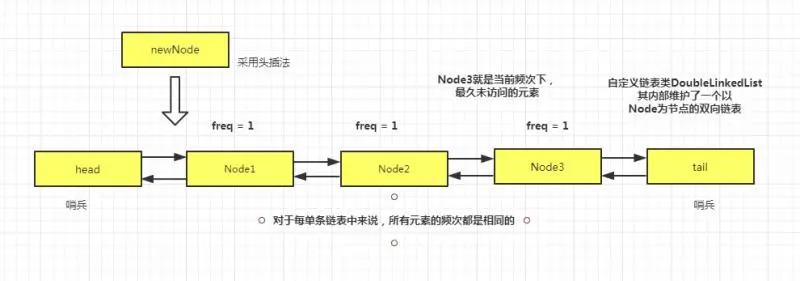
那么,这条双向链表,就需要维护当前频次下的所有元素的先后访问顺序。我们采用头插法,把新加入的元素添加到链表头部,这样的话,最久未访问的元素就在链表的尾部。
同样的,我们也用两个哨兵节点来代表头尾节点,以方便链表的操作。
代码如下:
- public class LFUCache2 {
- public static void main(String[] args) {
- LFUCache2 cache = new LFUCache2(2);
- cache.put(1, 1);
- cache.put(2, 2);
- // 返回 1
- System.out.println(cache.get(1));
- cache.put(3, 3); // 去除 key 2
- // 返回 -1 (未找到key 2)
- System.out.println(cache.get(2));
- // 返回 3
- System.out.println(cache.get(3));
- cache.put(4, 4); // 去除 key 1
- // 返回 -1 (未找到 key 1)
- System.out.println(cache.get(1));
- // 返回 3
- System.out.println(cache.get(3));
- // 返回 4
- System.out.println(cache.get(4));
- }
- private Map<Integer,Node> cache;
- private Map<Integer,DoubleLinkedList> freqMap;
- private int capacity;
- private int size;
- private int min;
- public LFUCache2(int capacity){
- this.capacity = capacity;
- cache = new HashMap<>();
- freqMap = new HashMap<>();
- }
- public int get(int key){
- Node node = cache.get(key);
- if(node == null) return -1;
- freqInc(node);
- return node.value;
- }
- public void put(int key, int value){
- if(capacity == 0) return;
- Node node = cache.get(key);
- if(node != null){
- node.value = value; //更新value值
- freqInc(node);
- }else{
- //若size达到最大值,则移除频次最小,最久未访问的元素
- if(size == capacity){
- //因链表是头插法,所以尾结点的前一个节点就是最久未访问的元素
- DoubleLinkedList list = freqMap.get(min);
- //需要移除的节点
- Node deadNode = list.tail.pre;
- cache.remove(deadNode.key);
- list.removeNode(deadNode);
- size--;
- }
- //新建一个node,并把node放到频次为 1 的 list 里面
- Node newNode = new Node(key,value);
- DoubleLinkedList newList = freqMap.get(1);
- if(newList == null){
- newList = new DoubleLinkedList();
- freqMap.put(1,newList);
- }
- newList.addNode(newNode);
- cache.put(key,newNode);
- size++;
- min = 1;//此时需要把min值重新设置为1
- }
- }
- //修改频次
- private void freqInc(Node node){
- //先删除node对应的频次list
- DoubleLinkedList list = freqMap.get(node.freq);
- if(list != null){
- list.removeNode(node);
- }
- //判断min是否等于当前node的频次,且当前频次的list为空,是的话更新min值
- if(min == node.freq && list.isEmpty()){
- min ++;
- }
- //然后把node频次加 1,并把它放到高频次list
- node.freq ++;
- DoubleLinkedList newList = freqMap.get(node.freq);
- if(newList == null){
- newList = new DoubleLinkedList();
- freqMap.put(node.freq, newList);
- }
- newList.addNode(node);
- }
- private class Node {
- int key;
- int value;
- int freq = 1;
- Node pre;
- Node next;
- public Node(){
- }
- public Node(int key, int value){
- this.key = key;
- this.value = value;
- }
- }
- //自实现的一个双向链表
- private class DoubleLinkedList {
- Node head;
- Node tail;
- // 设置两个哨兵节点,作为头、尾节点便于插入和删除操作
- public DoubleLinkedList(){
- head = new Node();
- tail = new Node();
- head.next = tail;
- tail.pre = head;
- }
- //采用头插法,每次都插入到链表的最前面,即 head 节点后边
- public void addNode(Node node){
- node.pre = head;
- node.next = head.next;
- //注意先把head的后节点的前节点设置为node
- head.next.pre = node;
- head.next = node;
- }
- //删除元素
- public void removeNode(Node node){
- node.pre.next = node.next;
- node.next.pre = node.pre;
- }
- //判断是否为空,即是否存在除了哨兵节点外的有效节点
- public boolean isEmpty(){
- //判断头结点的下一个节点是否是尾结点,是的话即为空
- return head.next == tail;
- }
- }
- }
方案五:用双向链表嵌套
思路:
可以发现方案三和方案四,都是用 freqmap 来存储频次和它对应的链表之间的关系,它本身也是一个哈希表。这次,我们完全用自己实现的双向链表来代替 freqMap,进一步提高效率。
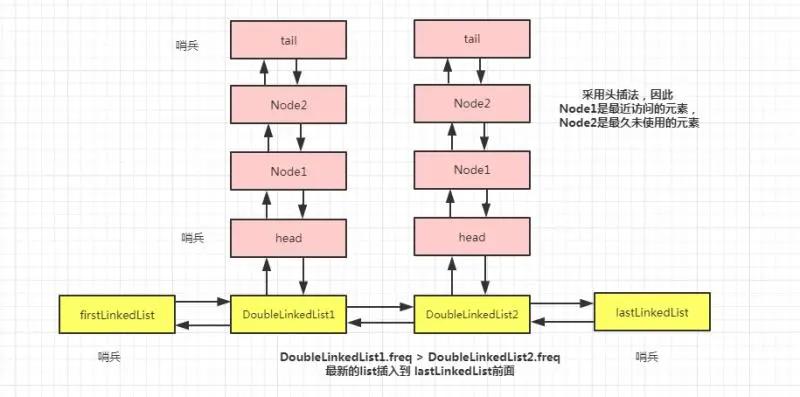
但是,结构有些复杂,它是一个双向链表中,每个元素又是双向链表。为了便于理解,我把它的结构作图如下:(为了方便,分别叫做外层链表,内层链表)
我们把整体看成一个由 DoubleLinkedList组成的双向链表,然后,每一个 DoubleLinkedList 对象中又是一个由 Node 组成的双向链表。像极了 HashMap 数组加链表的形式。
但是,我们这里没有数组,也就不存在哈希碰撞的问题。并且都是双向链表,都有哨兵存在,便于灵活的从链表头部或者尾部开始操作元素。
这里,firstLinkedList 和 lastLinkedList 分别代表外层链表的头尾结点。链表中的元素 DoubleLinkedList 有一个字段 freq 记录了频次,并且按照前大后小的顺序组成外层链表,即图中的 DoubleLinkedList1.freq 大于它后面的 DoubleLinkedList2.freq。
每当有新频次的 DoubleLinkedList 需要添加进来的时候,直接插入到 lastLinkedList 这个哨兵前面,因此 lastLinkedList.pre 就是一个最小频次的内部链表。
内部链表中是由 Node组成的双向链表,也有两个哨兵代表头尾节点,并采用头插法。其实,可以看到内部链表和方案四,图中所示的双向链表结构是一样的,不用多说了。
这样的话,我们就可以找到频次最小,并且最久未访问的元素,即
- //频次最小,最久未访问的元素,cache满时需要删除
- lastLinkedList.pre.tail.pre
于是,代码就好理解了:
- public class LFUCache3 {
- public static void main(String[] args) {
- LFUCache3 cache = new LFUCache3(2);
- cache.put(1, 1);
- cache.put(2, 2);
- // 返回 1
- System.out.println(cache.get(1));
- cache.put(3, 3); // 去除 key 2
- // 返回 -1 (未找到key 2)
- System.out.println(cache.get(2));
- // 返回 3
- System.out.println(cache.get(3));
- cache.put(4, 4); // 去除 key 1
- // 返回 -1 (未找到 key 1)
- System.out.println(cache.get(1));
- // 返回 3
- System.out.println(cache.get(3));
- // 返回 4
- System.out.println(cache.get(4));
- }
- Map<Integer,Node> cache;
- /**
- * 这两个代表的是以 DoubleLinkedList 连接成的双向链表的头尾节点,
- * 且为哨兵节点。每个list中,又包含一个由 node 组成的一个双向链表。
- * 最外层双向链表中,freq 频次较大的 list 在前面,较小的 list 在后面
- */
- DoubleLinkedList firstLinkedList, lastLinkedList;
- int capacity;
- int size;
- public LFUCache3(int capacity){
- this.capacity = capacity;
- cache = new HashMap<>();
- //初始化外层链表的头尾节点,作为哨兵节点
- firstLinkedList = new DoubleLinkedList();
- lastLinkedList = new DoubleLinkedList();
- firstLinkedList.next = lastLinkedList;
- lastLinkedList.pre = firstLinkedList;
- }
- //存储具体键值对信息的node
- private class Node {
- int key;
- int value;
- int freq = 1;
- Node pre;
- Node next;
- DoubleLinkedList doubleLinkedList;
- public Node(){
- }
- public Node(int key, int value){
- this.key = key;
- this.value = value;
- }
- }
- public int get(int key){
- Node node = cache.get(key);
- if(node == null) return -1;
- freqInc(node);
- return node.value;
- }
- public void put(int key, int value){
- if(capacity == 0) return;
- Node node = cache.get(key);
- if(node != null){
- node.value = value;
- freqInc(node);
- }else{
- if(size == capacity){
- /**
- * 如果满了,则需要把频次最小的,且最久未访问的节点删除
- * 由于list组成的链表频次从前往后依次减小,故最小的频次list是 lastLinkedList.pre
- * list中的双向node链表采用的是头插法,因此最久未访问的元素是 lastLinkedList.pre.tail.pre
- */
- //最小频次list
- DoubleLinkedList list = lastLinkedList.pre;
- //最久未访问的元素,需要删除
- Node deadNode = list.tail.pre;
- cache.remove(deadNode.key);
- list.removeNode(deadNode);
- size--;
- //如果删除deadNode之后,此list中的双向链表空了,则删除此list
- if(list.isEmpty()){
- removeDoubleLinkedList(list);
- }
- }
- //没有满,则新建一个node
- Node newNode = new Node(key, value);
- cache.put(key,newNode);
- //判断频次为1的list是否存在,不存在则新建
- DoubleLinkedList list = lastLinkedList.pre;
- if(list.freq != 1){
- DoubleLinkedList newList = new DoubleLinkedList(1);
- addDoubleLinkedList(newList,list);
- newList.addNode(newNode);
- }else{
- list.addNode(newNode);
- }
- size++;
- }
- }
- //修改频次
- private void freqInc(Node node){
- //从当前频次的list中移除当前 node
- DoubleLinkedList list = node.doubleLinkedList;
- if(list != null){
- list.removeNode(node);
- }
- //如果当前list中的双向node链表空,则删除此list
- if(list.isEmpty()){
- removeDoubleLinkedList(list);
- }
- //当前node频次加1
- node.freq++;
- //找到当前list前面的list,并把当前node加入进去
- DoubleLinkedList preList = list.pre;
- //如果前面的list不存在,则新建一个,并插入到由list组成的双向链表中
- //前list的频次不等于当前node频次,则说明不存在
- if(preList.freq != node.freq){
- DoubleLinkedList newList = new DoubleLinkedList(node.freq);
- addDoubleLinkedList(newList,preList);
- newList.addNode(node);
- }else{
- preList.addNode(node);
- }
- }
- //从外层双向链表中删除当前list节点
- public void removeDoubleLinkedList(DoubleLinkedList list){
- list.pre.next = list.next;
- list.next.pre = list.pre;
- }
- //知道了它的前节点,即可把新的list节点插入到其后面
- public void addDoubleLinkedList(DoubleLinkedList newList, DoubleLinkedList preList){
- newList.pre = preList;
- newList.next = preList.next;
- preList.next.pre = newList;
- preList.next = newList;
- }
- //维护一个双向DoubleLinkedList链表 + 双向Node链表的结构
- private class DoubleLinkedList {
- //当前list中的双向Node链表所有频次都相同
- int freq;
- //当前list中的双向Node链表的头结点
- Node head;
- //当前list中的双向Node链表的尾结点
- Node tail;
- //当前list的前一个list
- DoubleLinkedList pre;
- //当前list的后一个list
- DoubleLinkedList next;
- public DoubleLinkedList(){
- //初始化内部链表的头尾节点,并作为哨兵节点
- head = new Node();
- tail = new Node();
- head.next = tail;
- tail.pre = head;
- }
- public DoubleLinkedList(int freq){
- head = new Node();
- tail = new Node();
- head.next = tail;
- tail.pre = head;
- this.freq = freq;
- }
- //删除当前list中的某个node节点
- public void removeNode(Node node){
- node.pre.next = node.next;
- node.next.pre = node.pre;
- }
- //头插法将新的node插入到当前list,并在新node中记录当前list的引用
- public void addNode(Node node){
- node.pre = head;
- node.next = head.next;
- head.next.pre = node;
- head.next = node;
- node.doubleLinkedList = this;
- }
- //当前list中的双向node链表是否存在有效节点
- public boolean isEmpty(){
- //只有头尾哨兵节点,则说明为空
- return head.next == tail;
- }
- }
- }
由于,此方案全是链表的增删操作,因此时间复杂度可到 O(1)。
结语终于总结完了,其实,感觉思想搞明白了,代码实现起来就相对容易一些。但是,还是需要多写,多实践。过段时间再来回顾一下~
本文转载自微信公众号「 烟雨星空」,可以通过以下二维码关注。转载本文请联系 烟雨星空公众号。