普适逼近定理
众所周知,神经网络非常强大,可以将其用于几乎任何统计学习问题,而且效果很好。 但是您是否考虑过为什么会这样? 为什么在大多数情况下此方法比许多其他算法更强大?
与机器学习一样,这有一个精确的数学原因。 简而言之,神经网络模型描述的功能集非常大。 但是描述一组功能意味着什么? 一组功能如何大? 这些概念乍一看似乎很难理解,但是可以正确定义它们,从而阐明为什么某些算法比其他算法更好的原因。
机器学习作为函数逼近
让我们以一个抽象的观点来阐述什么是机器学习问题。 假设我们有数据集
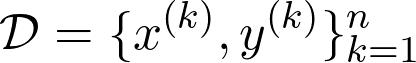
其中x⁽ᵏ⁾是数据点,y是与数据点相关的观测值。 观测值y⁽ᵏ⁾可以是实数,甚至可以是概率分布(在分类的情况下)。 任务只是找到一个函数f(x),对于该函数f(x⁽ᵏ⁾)近似为y⁽ᵏ⁾。
为此,我们预先修复了参数化的功能系列,然后选择最适合的参数配置。 例如,线性回归使用函数族
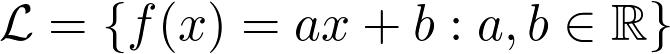
作为参数的函数族,以a和b为参数。
如果我们假设有一个真实的基础函数g(x)描述了x⁽ᵏ⁾和y⁽ᵏ⁾之间的关系,则该问题可以表述为函数逼近问题。 这将我们带入了美丽的近似理论技术领域。
近似理论入门
可能您一生中多次遇到指数函数。 它的定义是
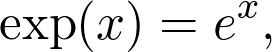
其中e是著名的欧拉数。 这是一个超越函数,基本上意味着您无法通过有限的多次加法和乘法来计算其值。 但是,当您将其放入计算器时,您仍然会获得价值。 该值仅是一个近似值,尽管对于我们的目的通常是足够的。 实际上,我们有
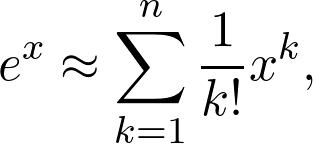
这是一个多项式,因此可以显式计算其值。 n越大,近似值越接近真实值。
逼近理论的中心问题是为这些问题提供数学框架。 如果您有任何函数g(x)以及从计算方面更易于处理的函数族,那么您的目标就是找到一个与g足够接近的"简单"函数。 本质上,近似理论搜索三个核心问题的答案。
- 什么是"足够接近"?
- 我可以(或应该)使用哪个函数系列来近似?
- 从给定的近似函数族中,哪一个确切的函数最适合?
别担心这些听起来是否有点抽象,因为接下来我们将研究神经网络的特殊情况。
神经网络作为函数逼近器
因此,让我们重申这个问题。 我们有一个函数g(x),它描述数据和观测值之间的关系。 这不是确切已知的,仅对于某些值
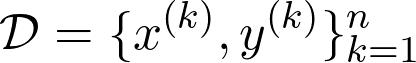
其中g(x⁽ᵏ⁾)=y⁽ᵏ⁾。 我们的工作是找到一个f(x)
- 从数据中概括知识
- 并且在计算上可行。
如果我们假设所有数据点都在子集X中,则
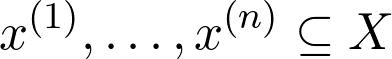
持有,我们想要一个数量最高准则的函数
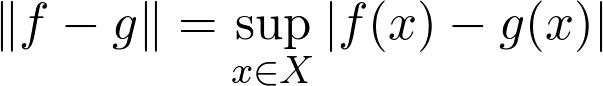
尽可能小。 您可以通过绘制这些函数,为图形包围的区域着色并计算沿y轴的最大扩展区域来想象这个数量。
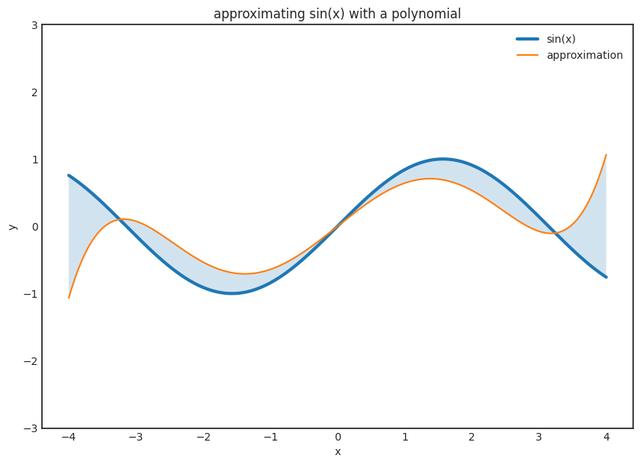
即使我们不能评估g(x)的任意值,我们也应该始终在更广泛的意义上接近它,而不是要求f(x)仅适合已知数据点xₖ。
因此,给出了问题。 问题是,我们应该使用哪一组函数进行近似?
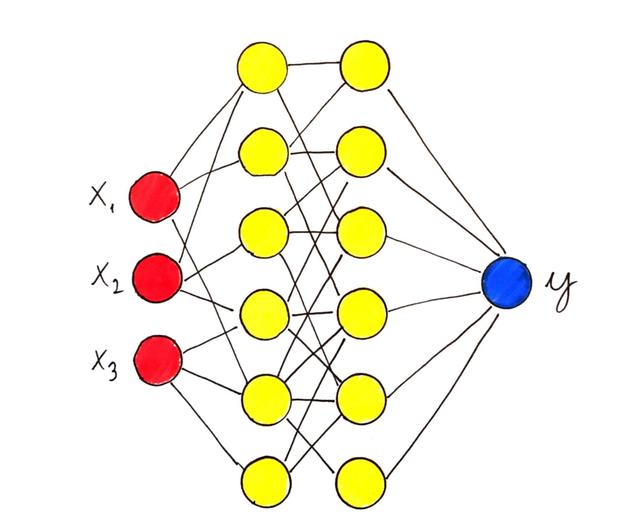
具有单个隐藏层的神经网络
从数学上讲,具有单个隐藏层的神经网络定义为
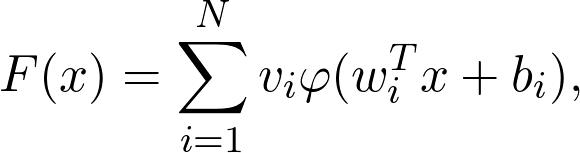
其中φ是非线性函数(称为激活函数),例如S型函数
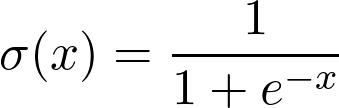
和
值x对应于数据,而wᵢ,bᵢ和vᵢ是参数。 是功能家族
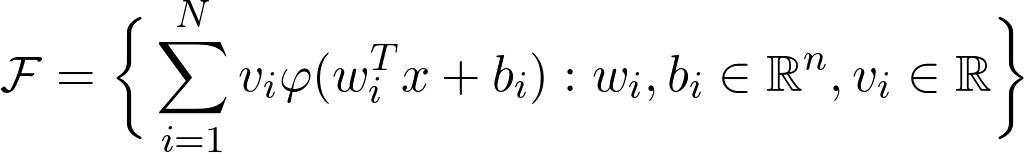
足以近似任何合理的功能? 答案是肯定的!
普适逼近定理
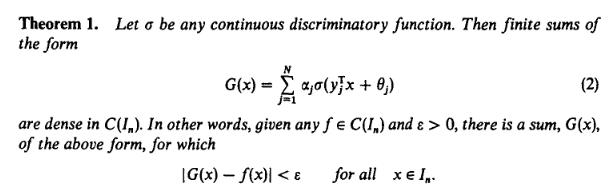
- > The universal approximation theorem in its full glory :) Source: Cybenko, G. (1989) "Approximations by superpositions of sigmoidal functions", Mathematics of Control, Signals, and Systems, 2(4), 303–314.
1989年的一个著名结果被称为通用逼近定理,该结论指出,只要激活函数像S形函数且被逼近的函数是连续的,具有单个隐藏层的神经网络就可以根据需要精确地对其进行逼近。 (或使用机器学习术语进行学习。)
如果确切的定理似乎很困难,请不要担心,我将详细解释整个过程。 (实际上,我故意跳过了稠密之类的概念,以使说明更清晰,尽管不够精确。)
步骤1。 假设要学习的函数是g(x),它是连续的。 让我们固定一个小的ε并在函数周围绘制一个ε宽的条纹。 ε越小,结果越好。
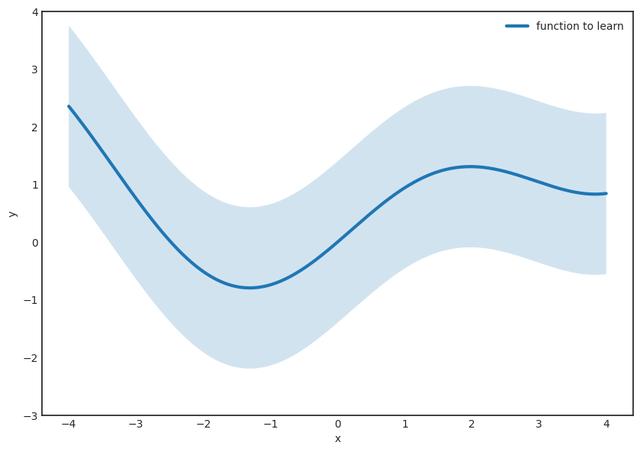
第二步。 (最困难的部分。)找到表格的功能
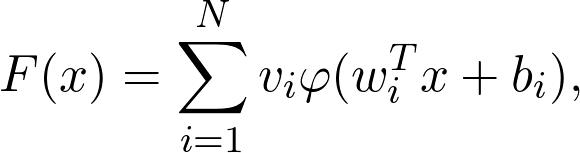
完全在条纹内 该定理保证了这样的F(x)的存在,因此这个函数族被称为通用逼近器。 这是神经网络的真棒,赋予它们真正的力量。
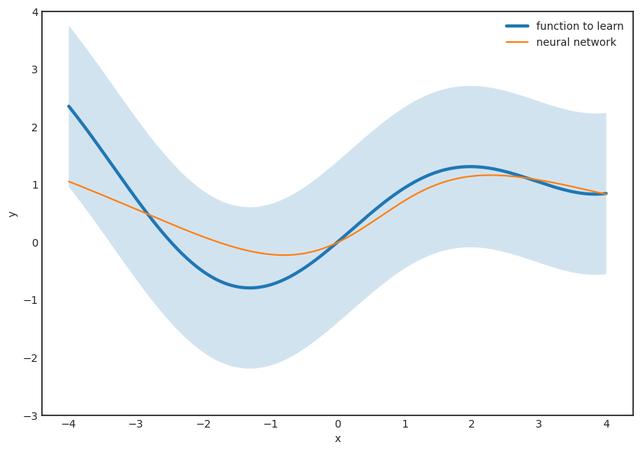
但是,有几个警告。 例如,该定理没有说出N,也就是隐藏层中神经元的数量。 对于较小的ε,它可能非常大,从计算角度来看这是不利的。 我们希望尽快计算预测,而计算100亿项之和绝对不好玩。
第二个问题是,即使该定理保证了一个良好的逼近函数的存在,也没有告诉我们如何找到它。 尽管这可能令人惊讶,但这在数学中是非常典型的。 我们有非常强大的工具来推断某些对象的存在,而又不能显式构造它们。 (有一所称为建构主义的数学学校,它拒绝纯粹的存在性证明,例如通用逼近定理的原始证明。但是,这个问题根深蒂固。如果不接受非构造性证明,我们甚至无法谈论 无限集上的函数。)
但是,最大的问题是,在实践中,我们永远不会完全了解底层功能,而只会知道所观察到的内容:
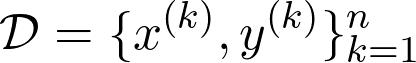
有无数种可能的配置可以很好地适合我们的数据。 它们中的大多数可怕地概括为新数据。 您肯定知道这种现象:这是可怕的过度拟合。
拥有权利的同时也被赋予了重大的责任
所以,这是东西。 如果您有N个观测值,则可以找到一个非常适合您的观测值的N-1阶多项式。 这没什么大不了的,您甚至可以使用Lagrange插值明确地写下该多项式。 但是,它不会推广到任何新数据,实际上会很糟糕。 下图展示了当我们尝试将大多项式拟合到一个小的数据集时会发生什么。
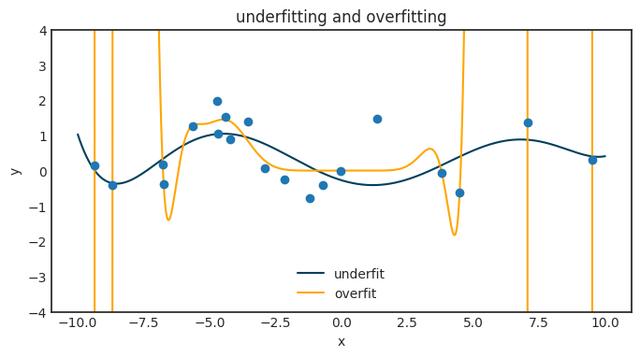
神经网络也有同样的现象。 这是一个巨大的问题,而通用逼近定理给我们关于如何克服这一问题的绝对零提示。
通常,功能族的表现力越高,就越容易过度拟合。 拥有权利的同时也被赋予了重大的责任。 这称为偏差方差折衷。 对于神经网络,从权重的L1正则化到下降层,有很多方法可以缓解这种情况。 但是,由于神经网络具有如此高的表现力,因此这个问题始终在后台隐约可见,需要不断关注。
超越万能逼近定理
正如我已经提到的,该定理没有提供任何工具来为我们的神经网络找到参数配置。 从实际的角度来看,这几乎与通用逼近性质一样重要。 几十年来,神经网络一直不受欢迎,因为缺乏一种计算有效的方法来使它们适合数据。 有两项重要的进步,使它们的使用成为可能:反向传播和通用GPU-s。 有了这两个工具,训练庞大的神经网络变得轻而易举。 您可以使用笔记本训练最先进的模型,甚至不费吹灰之力。 自从通用逼近定理以来,我们已经走到现在!
通常,这是标准深度学习课程的起点。 由于其数学上的复杂性,因此未涵盖神经网络的理论基础。 但是,通用逼近定理(及其证明中使用的工具)对神经网络为何如此强大提供了非常深入的了解,甚至为工程新颖的体系结构奠定了基础。 毕竟,谁说过我们只能将S型和线性函数结合起来?