本文转载自公众号“读芯术”(ID:AI_Discovery)
在三行函数中解决任何线性方程式的技巧,甚至可以在两行代码中重写,不想了解一下嘛?据笔者所知,这是解决Python中线性方程的最有效方法。
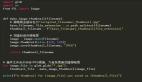
- defsolve_linear(equation,var='x'):
- expression =equation.replace("=","-(")+")"
- grouped =eval(expression.replace(var,'1j'))
- return -grouped.real/grouped.imag

这是标准代数过程示例,最后得出答案。
它的原理是怎样的呢?首先定义一个线性方程式,它必须以纯形式可解。这意味着它只能有一个变量,通常写为x。二元方程需要求解多个线性方程(方程组)。
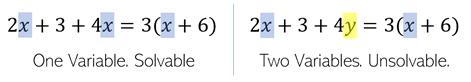
线性方程式由三个主要部分组成:常数,变量和乘数。
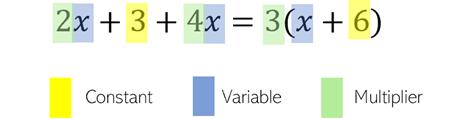
不管是几元方程还是运算的组合(加,减,乘和除),在括号范围内都是有效的。只要遵守线性方程的这些定义,就可以通过函数解决。

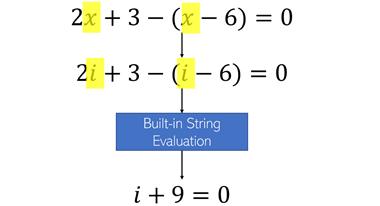
接下来逐步分解该函数,用以下线性方程式的演示为例。
将第一行中等式右侧的整个表达式移到左侧,将等式转换为要求值的表达式。
- expression= equation.replace("="," - (")+")"
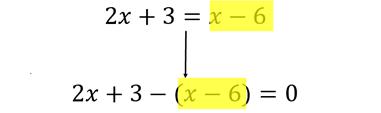
IDE中的演示如下:

等式中的所有“变量”已移至一侧,等号后已无变量,该表达式等于0。
在第二行代码中计算新表达式的值,表示为ax + b =0。使用Python的内置复数处理,其中j表示数学常数i =√-1。
- grouped= eval(expression.replace(var,'1j')
注意,在函数初始化时将var指定为x。
eval函数有一个表达式。通过用已知的j(i)替换未知变量x,Python将两类表达式元素分开求值,即变量和常量。对表达式求值时,答案为a * j +b,Python认定这是一个复数。由于使用j代替了x,所以结果是一个简化且易于求解的线性方程。
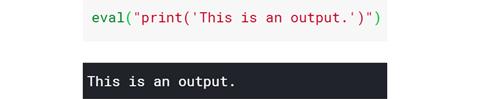
首先,在eval()的演示工作流程中,它可以接收字符串中给出的任何Python命令:
因此,数学表达式与任何Python表达式的处理方式相同。eval()的独到之处在于无需手动执行繁重的工作,而是利用Python的字符串处理。
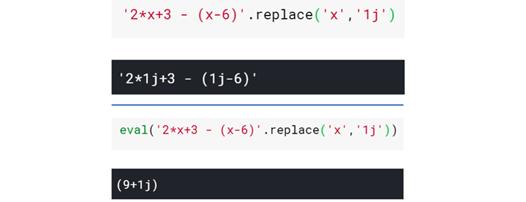
Python会认为x实际上是i来自动求值字符串,这与下图中的操作相同:
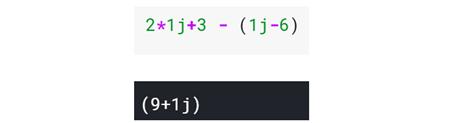
最后获得了简化形式ax + b = 0。通过标准和简单的代数运算,发现x等于-b / a,或者通过创建的复数来运算,实数部分的负数(上例中为9)除以虚数乘数(上例中为1)。
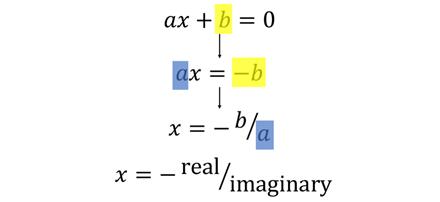
- return -grouped.real/grouped.imag
在最后一行代码中,通过返回复数实数部分的负数除以虚数部分来简单地返回此代数步骤。
通过操纵和利用Python的内置数学求值功能,这三行函数就可以对任何线性方程式(无论其长度或复杂度)进行处理啦。