前言
斐波那契数列是一个很经典的问题,虽然它很简单,但是在优化求解它的时候可以延伸出很多实用的优化算法。
它的概念很简单,来看一下 LeetCode 真题里对他的定义:
斐波那契数,通常用 F(n) 表示,形成的序列称为斐波那契数列。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
给定 N,计算 F(N)。
先大概预览一下斐波那契数列的样子:
- 1、1、2、3、5、8、13、21、34
青铜时代 - 递归求解。
在本文中,下面出现的 fib(n) 代表对于 n 的求解。
有了定义以后,对于这个问题我们第一直觉就是可以用「递归」来解,思路也很简单,只需要定义好初始状态,也就是 fib(1) = 1,fib(2) = 1,那么假设要求 fib(3) 只需要去求 fib(2) + fib(1) 即可,以此类推。
大概在 fib(50) 的时候,在我的笔记本上跑了 123.167 秒,再往后就更加不敢想象了。由于大量的递归调用加上不断的重复计算,导致这个算法的速度慢到不可接受。
白银时代 - 备忘录解法
青铜的解法由于有大量的重复计算,
比如 fib(3) 会计算 fib(2) + fib(1),
而 fib(2) 又会计算 fib(1) + fib(0)。
这个 fib(1) 就是完全重复的计算,不应该为它再递归调用一次,而是应该在第一次求解除它了以后,就把他“记忆”下来。
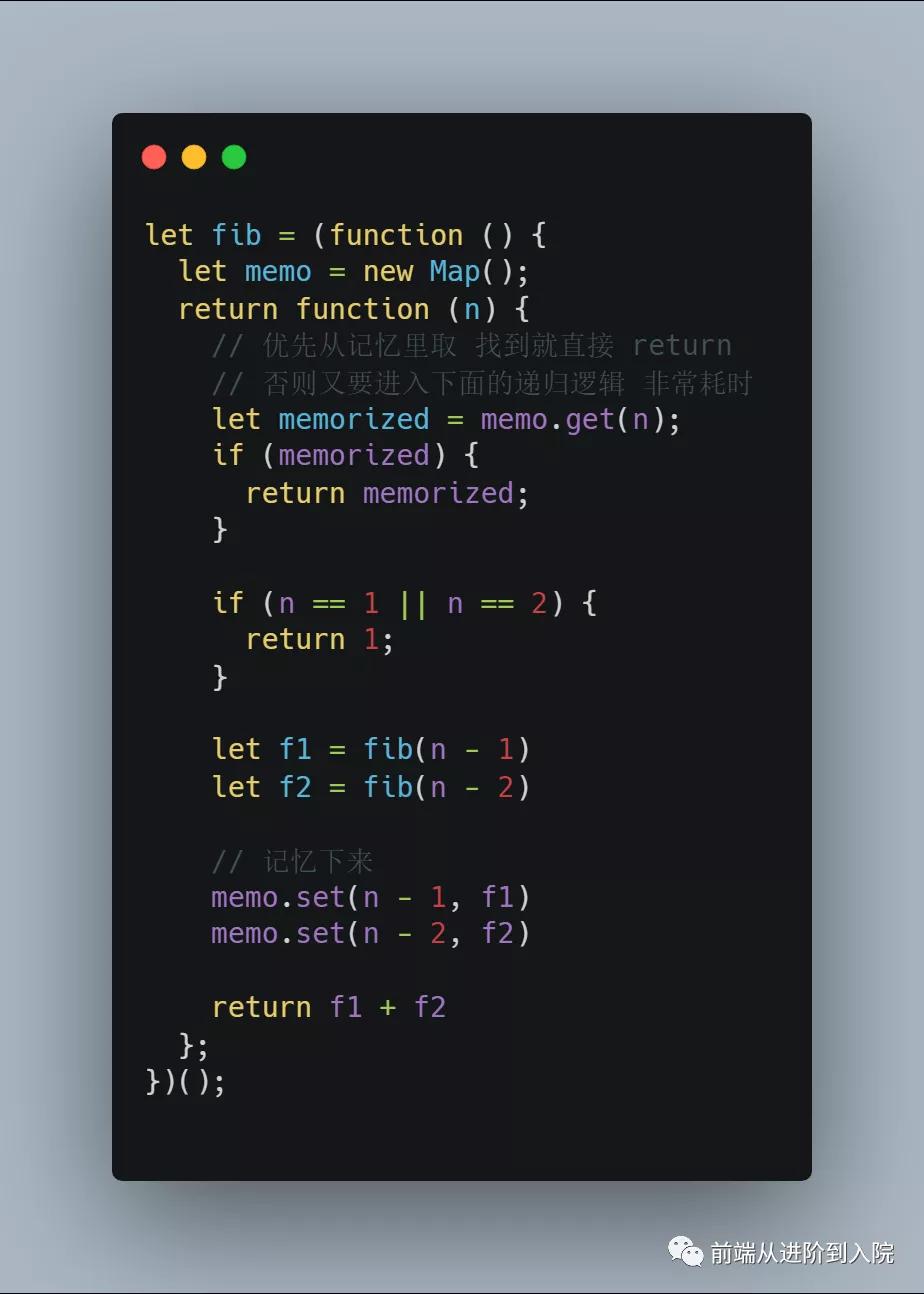
把已经求得的解放在 Map 里,下次直接取,而不去重复结算。
这里用 iife 函数形成一个闭包,保留了 memo 这个私有变量,这是一个小技巧。
此时对于 fib(50) 的计算速度来到了 0.096 秒,在 50 这个小数量级的情况下就比青铜解法快了 1200 倍。
有一部分说算法无用论的人,持有的观点是随着硬件的进步这些差异都会被抹平,那我期待着硬件进步 1000 倍的那一天吧。
黄金时代 - 动态规划
看似上面的备忘录解法已经很完美了,实际上不是,虽然备忘录解法把无用的重复求解都优化了,在速度上达到了比较优的程度。
但是对于第一次求解,未被记忆化的值来说,还是会进入递归调用逻辑。
比如 f(10000),那么必然会递归调用 f(9999)、f(9998) ...... f(0),而在递归的过程中,这些调用栈是不断叠加的,当函数调用的深处,栈已经达到了成千上万层。
此时它就会报出一个我们熟悉的错误:
- RangeError: Maximum call stack size exceeded
- at c:\codes\leetcode-javascript\动态规划\斐波那契数列-509.js:20:19
- at c:\codes\leetcode-javascript\动态规划\斐波那契数列-509.js:32:14
我们回过头来思考一下,备忘录的思路下我们的解法路径是「自顶向下」的,如果我们把思路倒置一下,变成「自底向上」的求解呢?
也就是说,对于 fib(10000),我们从 fib(1), fib(2), fib(3) ...... fib(10000),
从最小的值开始求解,并且把每次求解的值保存在“记忆”(可以是一个数组,下标正好用来对应 n 的解答值)里,下面的值都由记忆中的值直接得出。
这样等到算到 10000 的时候,我们想要求解的值自然也就得到了,直接从 记忆[10000] 里取到值返回即可。
那么这种解法其实只需要一个 for 循环,而不需要任何递归的逻辑。
其实这就是「动态规划」的一种比较经典的解法啦,那么这种算法强力吗?
对于 fib(10000) 这个上面两种解法都无能为力的情况来说,它花了 0.114 秒就得出了结果。
对于 fib(100000) 它花了 0.827 秒。
对了,在 JavaScript 中这个数字由于超出最大值,会被展示成 Infinity,其实解决方法也很简单,用 BigInt 的数据类型即可。
总结
本文用一个简单的斐波那契数列的例子来体会了动态规划算法的美感,以及它的强大能力。相信看完这篇文章的你,能够知道算法并不是用来炫技的,而是真切的可以解决效率问题的。