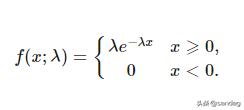介绍
拥有良好的统计背景对于数据科学家的日常工作可能会大有裨益。每次我们开始探索新的数据集时,我们首先需要进行探索性数据分析(EDA),以了解某些特征的概率分布是什么。如果我们能够了解数据分布中是否存在特定模式,则可以量身定制最适合我们的机器学习模型。这样,我们将能够在更短的时间内获得更好的结果(减少优化步骤)。实际上,某些机器学习模型被设计为在某些分布假设下效果最佳。因此,了解我们正在使用哪个概率分布可以帮助我们确定最适合使用哪些模型。
不同类型的数据
每次我们使用数据集时,我们的数据集都会代表总体的样本。然后使用这个样本,我们可以尝试了解其概率分布,以便我们可以使用它对总体进行预测。
假设我们要根据一组数据来预测房屋的价格,我们可以找到一个包含旧金山所有房价的数据集(我们的样本),进行一些统计分析之后,我们就可以对美国其他任何城市的房价做出相当准确的预测(我们的总体)。
数据集由两种主要类型的数据组成:数值(例如整数,浮点数)和标签(例如名字,电脑品牌)。
数值数据还可以分为其他两类:离散和继续。离散数据只能采用某些值(例如,学校中的学生人数),而连续数据可以采用任何实际或分数值(例如,身高和体重的概念)。
从离散随机变量中,可以计算出概率质量函数,而从连续随机变量中,可以得出概率密度函数。
概率质量函数给出了变量可以等于某个值的概率,概率密度函数的值本身并不是概率,需要在给定范围内进行积分。
自然界中存在许多不同的概率分布,在本文中,我将向大家介绍数据科学中最常用的概率分布。
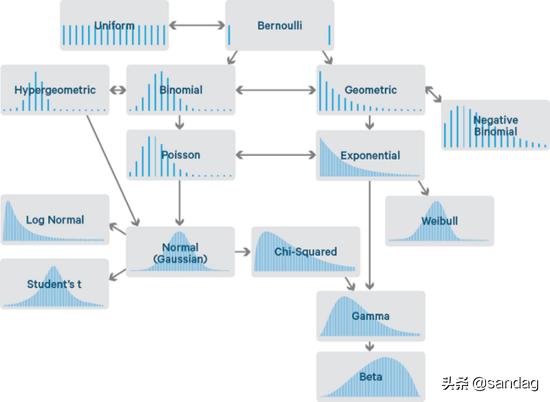
在本文中,我将提供有关如何创建每个不同概率分布的代码。首先,让我们导入所有必要的库:
- import pandas as pd
- import numpy as np
- import matplotlib.pyplot as plt
- import scipy.stats as stats
- import seaborn as sns
伯努利分布
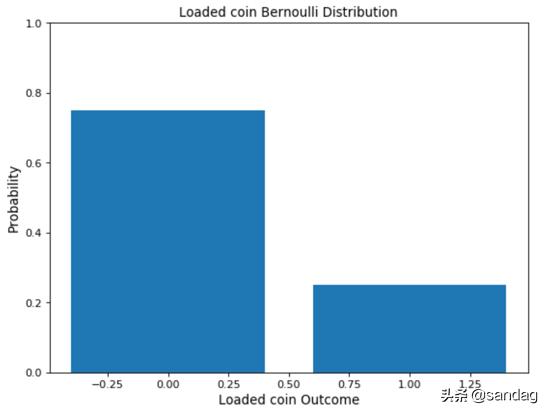
伯努利分布是最容易理解的分布之一,可用作导出更复杂分布的起点。这种分布只有两个可能的结果,一个简单的例子就是抛掷偏斜/无偏硬币。在此示例中,可以认为结果可能是正面的概率等于p,而对于反面则是(1-p)(包含所有可能结果的互斥事件的概率总和为1)。
- probs = np.array([0.75, 0.25])
- face = [0, 1]
- plt.bar(face, probs)
- plt.title('Loaded coin Bernoulli Distribution', fontsize=12)
- plt.ylabel('Probability', fontsize=12)
- plt.xlabel('Loaded coin Outcome', fontsize=12)
- axes = plt.gca()
- axes.set_ylim([0,1])
均匀分布
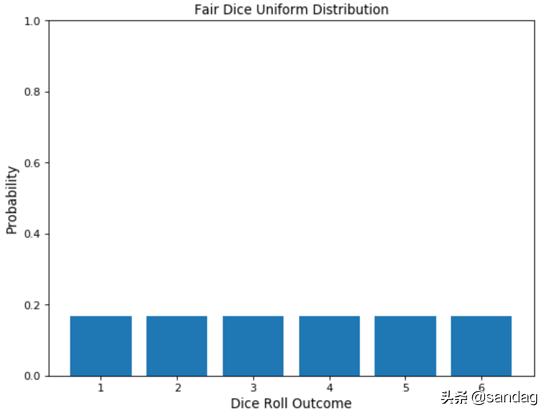
均匀分布可以很容易地从伯努利分布中得出。在这种情况下,结果的数量可能不受限制,并且所有事件的发生概率均相同。例如掷骰子,存在多个可能的事件,每个事件都有相同的发生概率。
- probs = np.full((6), 1/6)
- face = [1,2,3,4,5,6]
- plt.bar(face, probs)
- plt.ylabel('Probability', fontsize=12)
- plt.xlabel('Dice Roll Outcome', fontsize=12)
- plt.title('Fair Dice Uniform Distribution', fontsize=12)
- axes = plt.gca()
- axes.set_ylim([0,1])
二项分布
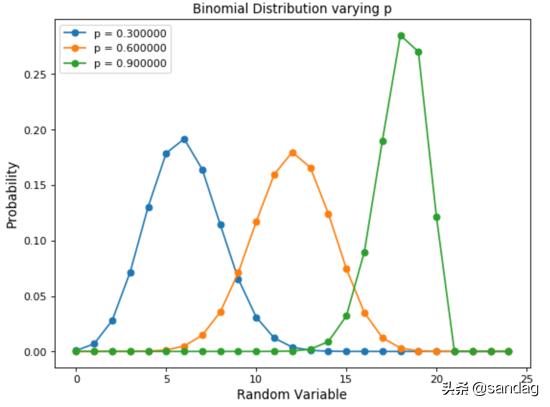
二项分布被认为是遵循伯努利分布的事件结果的总和。因此,二项分布用于二元结果事件,并且所有后续试验中成功和失败的概率均相同。此分布采用两个参数作为输入:事件发生的次数和试验成功与否的概率。二项式分布最简单的示例就是将有偏/无偏硬币抛掷一定次数。
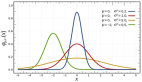
大家可以观察一下不同概率情况下二项分布的图形:
- # pmf(random_variable, number_of_trials, probability)
- for prob in range(3, 10, 3):
- x = np.arange(0, 25)
- binom = stats.binom.pmf(x, 20, 0.1*prob)
- plt.plot(x, binom, '-o', label="p = {:f}".format(0.1*prob))
- plt.xlabel('Random Variable', fontsize=12)
- plt.ylabel('Probability', fontsize=12)
- plt.title("Binomial Distribution varying p")
- plt.legend()
二项式分布的主要特征是:
- 给定多个试验,每个试验彼此独立(一项试验的结果不会影响另一项试验)。
- 每个试验只能得出两个可能的结果(例如,获胜或失败),其概率分别为p和(1- p)。
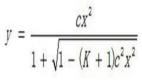
如果获得成功概率(p)和试验次数(n),则可以使用以下公式计算这n次试验中的成功概率(x)。
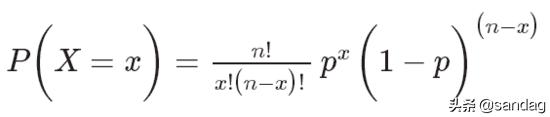
正态(高斯)分布
正态(高斯)分布是数据科学中最常用的分布之一。
我们日常生活中发生的许多常见现象都遵循正态分布,例如:经济中的收入分布,学生的平均报告数量,平均身高等。此外,中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。
- n = np.arange(-50, 50)
- mean = 0
- normal = stats.norm.pdf(n, mean, 10)
- plt.plot(n, normal)
- plt.xlabel('Distribution', fontsize=12)
- plt.ylabel('Probability', fontsize=12)
- plt.title("Normal Distribution")
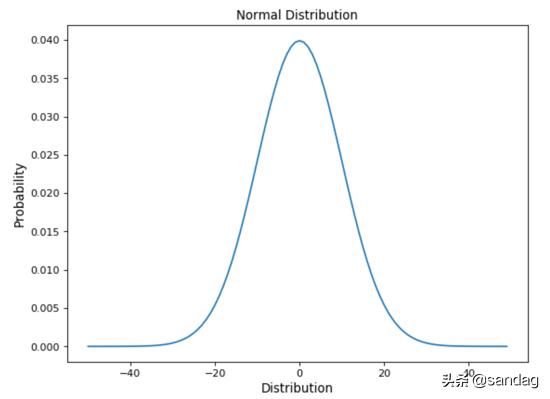
可以看出正态分布的特征:
- 曲线在中心对称。 因此,均值,众数和中位数都相等,从而使所有值围绕均值对称分布。
- 分布曲线下的面积等于1(所有概率之和必须等于1)
可以使用以下公式得出正态分布

使用正态分布时,均值和标准差起着非常重要的作用。如果我们知道它们的值,通过概率分布即可轻松找出预测精确值的概率。根据正态分布的特性,68%的数据位于均值的一个标准差范围内,95%的数据位于均值的两个标准差范围内,99.7%的数据位于均值的三个标准差范围内。
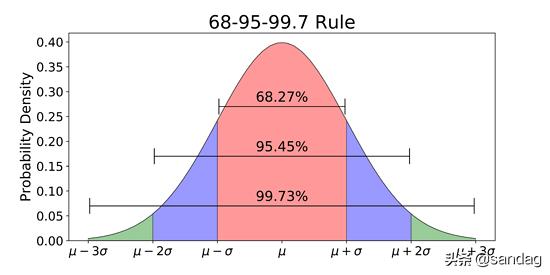
许多机器学习模型被设计为遵循正态分布有最佳效果。以下是一些示例:
- 高斯朴素贝叶斯分类器
- 线性判别分析
- 二次判别分析
- 基于最小二乘的回归模型
在某些情况下可以通过对数和平方根等变换将非正态数据转换为正态形式。
泊松分布
泊松分布通常用于查找事件可能发生或不发生的频率,还可用于预测事件在给定时间段内可能发生多少次。
例如,保险公司经常使用泊松分布来进行风险分析(预测在预定时间段内发生的车祸事故数),以决定汽车保险的定价。
当使用泊松分布时,我们可以确信发生不同事件之间的平均时间,但是事件发生的确切时刻在时间上是随机间隔的。
泊松分布可以使用以下公式建模,其中λ表示单位时间(或单位面积)内随机事件的平均发生率。
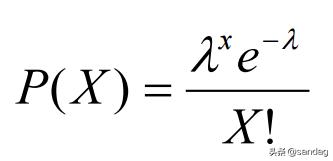
泊松分布的主要特征是:
- 事件彼此独立
- 一个事件可以发生任何次数(在定义的时间段内)
- 两个事件不能同时发生
- 事件发生之间的平均发生率是恒定的。
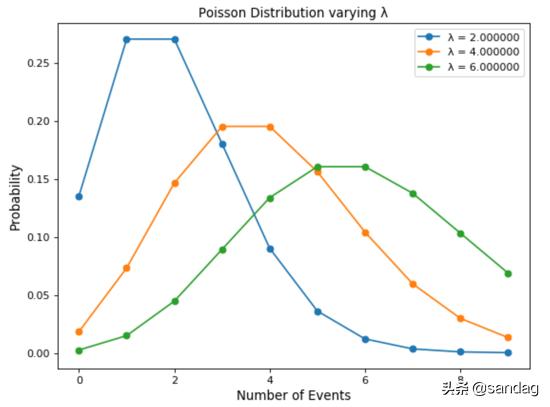
下图显示了改变λ的值是如何影响泊松分布的:
- for lambd in range(2, 8, 2):
- n = np.arange(0, 10)
- poisson = stats.poisson.pmf(n, lambd)
- plt.plot(n, poisson, '-o', label="λ = {:f}".format(lambd))
- plt.xlabel('Number of Events', fontsize=12)
- plt.ylabel('Probability', fontsize=12)
- plt.title("Poisson Distribution varying λ")
- plt.legend()
指数分布
指数分布用于对不同事件之间的时间进行建模。
举例来说,假设我们在一家餐厅工作,并且希望预测不同顾客来就餐的时间间隔。针对此类问题使用指数分布一个理想的起点。指数分布的另一个常见应用是生存分析(例如设备/机器的预期寿命)。
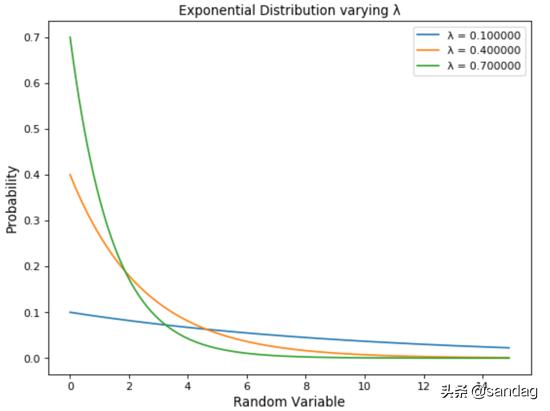
指数分布由参数λ调节。λ值越大,曲线的斜率变化越快。
- for lambd in range(1,10, 3):
- x = np.arange(0, 15, 0.1)
- y = 0.1*lambd*np.exp(-0.1*lambd*x)
- plt.plot(x,y, label="λ = {:f}".format(0.1*lambd))
- plt.xlabel('Random Variable', fontsize=12)
- plt.ylabel('Probability', fontsize=12)
- plt.title("Exponential Distribution varying λ")
- plt.legend()
指数分布使用以下公式建模