前言
这次我们介绍另一种时间复杂度为 O(nlogn) 的选择类排序方法叫做堆排序。
我将从以下几个方面介绍:
- 堆的结构
- 堆排序
- 优化的堆排序
- 原地堆排序
- 堆的应用
堆的结构
什么是堆?我给出了百度的定义,如下:
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵 完全二叉树 的数组对象。
堆总是满足下列性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值。
- 堆总是一棵完全二叉树。
将根节点最大的堆叫做最大堆,根节点最小的堆叫做最小堆。
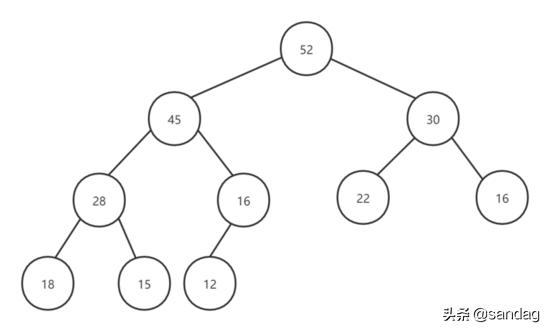
下图展示了一个最大堆的结构:
可见,堆中某个节点的值总是小于等于其父节点的值。
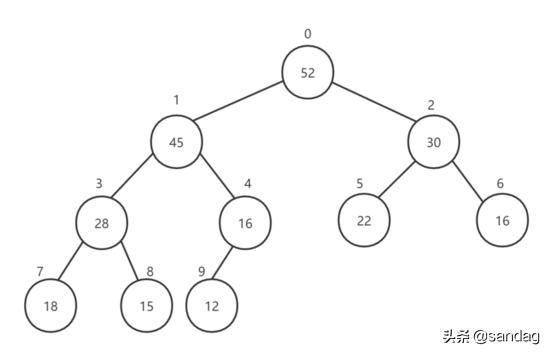
由于堆是一棵完全二叉树,因此我们可以对每一层进行编号,如下:
我们完全可以使用数组存放这些元素,那如何确定存放的位置呢?利用如下公式:
- 父节点:parent(i) = (i-1)/2
- 左孩子:leftChild(i) = 2*i+1
- 右孩子:rightChild(i) = 2*i+2
相关代码如下:
- private int parent(int index) {
- return (index - 1) / 2;
- }
- private int leftChild(int index) {
- return index * 2 + 1;
- }
- private int rightChild(int index) {
- return index * 2 + 2;
- }
添加元素
向堆中添加元素的步骤如下:
- 将新元素放到数组的末尾。
- 获取新元素的父亲节点在数组中的位置,比较新元素和父亲节点的值,如果父亲节点的值小于新元素的值,那么两者交换。以此类推,不断向上比较,直到根节点结束。
下图展示了添加元素的过程:
添加元素的过程也叫做 siftUp ,代码如下:
- // Array是自己实现的动态数组
- private Array<E> data;
- public void add(E e) {
- data.addLast(e);
- siftUp(data.getSize() - 1);
- }
- private void siftUp(int k) {
- while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
- data.swap(k, parent(k));
- k = parent(k);
- }
- }
删除元素
删除元素其实就是删除堆顶的元素,步骤如下:
- 让数组最后一个元素和数组第一个元素(堆顶元素)交换。
- 交换完后,删除数组最后的元素。
- 让堆顶元素和左右孩子节点比较,如果堆顶元素比左右孩子节点中最大的元素还要大,那么满足堆的性质,直接退出。否则如果堆顶元素比左右孩子节点中最大的元素小,那么堆顶元素就和最大的元素交换,然后继续重复执行以上操作,只不过这时候把堆顶元素称为父节点更好。
下图展示了删除元素的过程:
删除元素的过程也叫做 siftDown ,代码如下:
- // 这里我们不命名为remove,命名为extractMax,抽取堆顶最大元素
- public E extractMax() {
- E ret = findMax();
- // 让最后一个叶子节点补到根节点,然后让它下沉
- // (为什么是取最后一个叶子节点,因为即使取走最后一个叶子节点,依旧能保持是一棵完全二叉树)
- data.swap(0, data.getSize() - 1);
- data.removeLast();
- siftDown(0);
- return ret;
- }
- private void siftDown(int k) {
- while (leftChild(k) < data.getSize()) {
- int j = leftChild(k);
- if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) {
- j = rightChild(k);
- // data[j]是leftChild和rightChild中的最大值
- }
- // 如果父节点比左右孩子中的最大值还要大,那么说明没有问题,直接退出
- if (data.get(k).compareTo(data.get(j)) >= 0) {
- break;
- }
- // 否则交换
- data.swap(k, j);
- k = j;
- }
- }
最大堆的完整代码
堆排序
通过上面的介绍,我们应该明白了堆的结构,堆的添加和删除元素操作是如何完成的。那么对于堆排序来说,就是小菜一碟了,因为堆排序就是用到了堆的添加和删除操作,步骤如下:
- 将数组中元素一个个添加到堆(最大堆)中。
- 添加完成后,每次取出一个元素倒序放入到数组中。
堆排序代码:
- ublic static void sort(Comparable[] arr) {
- int n = arr.length;
- // MaxHeap是自己实现的最大堆
- MaxHeap<Comparable> maxHeap = new MaxHeap<>(n);
- for (int i = 0; i < n; i++) {
- maxHeap.add(arr[i]);
- }
- for (int i = n - 1; i >= 0; i--) {
- arr[i] = maxHeap.extractMax();
- }
- }
堆排序完整代码
优化的堆排序
在上述的堆排序中,我们在将数组中元素添加到堆时,都是一个个添加,是否有优化的方法呢?答案是有的,我们可以将数组直接转换成堆,这种操作叫做 Heapify 。
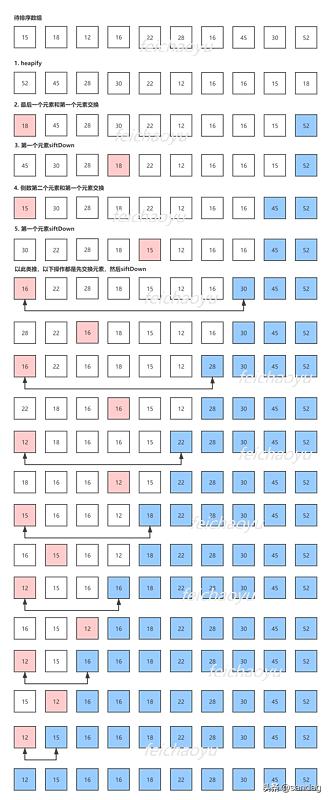
Heapify 就是从最后一个节点开始,判断父节点是否比孩子节点大,不是就 siftDown 。 Heapify 操作的时间复杂度是 O(n) ,相比一个个添加的时间复杂度是 O(nlogn) ,可见性能提升了不少。
假设我们有数组: [15, 18, 12, 16, 22, 28, 16, 45, 30, 52] ,下图展示了对其进行 Heapify 的过程。
优化的堆排序代码:
- public static void sort(Comparable[] arr) {
- int n = arr.length;
- // MaxHeap是自己实现的最大堆,当传入数组作为构造参数时,会对其进行heapify
- MaxHeap<Comparable> maxHeap = new MaxHeap<>(arr);
- for (int i = n - 1; i >= 0; i--) {
- arr[i] = maxHeap.extractMax();
- }
- }
- // 构造方法
- public MaxHeap(E[] arr) {
- data = new Array<>(arr);
- // 将数组堆化的过程就是从最后一个节点开始,判断父节点是否比子节点大,不是就siftDown
- for (int i = parent(arr.length - 1); i >= 0; i--) {
- siftDown(i);
- }
- }
优化的堆排序完整代码
原地堆排序
原地堆排序可以让我们的空间复杂度变为 O(1) ,因为不占用新的数组。
原地堆排序类似于堆的删除元素,步骤如下:
- Heapify
- siftDown
- siftDown
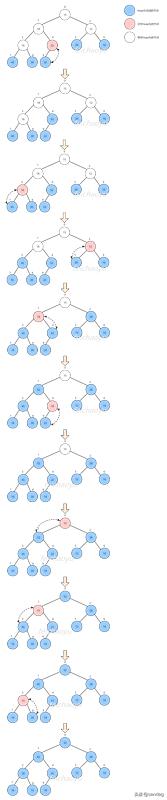
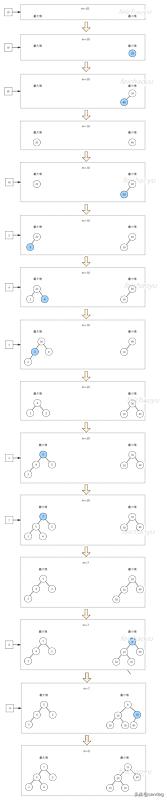
下图展示了原地堆排序的过程:
原地堆排序代码:
- public static void sort(Comparable[] arr) {
- int n = arr.length;
- // heapify
- for (int i = parent(n-1); i >= 0; i--) {
- siftDown(arr, n, i);
- }
- // 核心代码
- for (int i = n - 1; i > 0; i--) {
- swap(arr, 0, i);
- siftDown(arr, i, 0);
- }
- }
- private static void swap(Object[] arr, int i, int j) {
- Object t = arr[i];
- arr[i] = arr[j];
- arr[j] = t;
- }
- private static void siftDown(Comparable[] arr, int n, int k) {
- while (leftChild(k) < n) {
- int j = leftChild(k);
- if (j + 1 < n && arr[j + 1].compareTo(arr[j]) > 0) {
- j = rightChild(k);
- }
- // 如果父节点比左右孩子中的最大值还要大,那么说明没有问题,直接退出
- if (arr[k].compareTo(arr[j]) >= 0) {
- break;
- }
- // 否则交换
- swap(arr, k, j);
- k = j;
- }
- }
原地堆排序完整代码
堆的应用
优先级队列
一旦我们掌握了堆这个数据结构,那么优先级队列的实现就很简单了,只需要弄清楚优先级队列需要有哪些接口就行。JDK 中自带的 PriorityQueue 就是用堆实现的优先级队列,不过需要注意 PriorityQueue 内部使用的是最小堆。
优先级队列完整代码
Top K 问题
Top K 问题就是求解 前 K 个 最大的元素或者最小的元素。元素个数不确定,数据量可能很大,甚至源源不断到来,但需要知道目前为止前 K 个最大或最小的元素。当然问题还可能变为求解 第 K 个 最大的元素或最小的元素。
通常我们有如下解决方案:
- 使用JDK中自带的排序,如 Arrays.sort() ,由于底层使用的快速排序,所以时间复杂度为 O(nlogn) 。但是如果 K 取值很小,比如是 1,即取最大值,那么对所有元素排序就没有必要了。
- 使用简单选择排序,选择 K 次,那么时间复杂度为 O(n*K) ,如果 K 大于 logn,那还不如快排呢!
上述两种思路都是假定所有元素已知,如果元素个数不确定,且数据源源不断到来的话,就无能为力了。
下面提供一种新的思路:
我们维护一个长度为 K 的数组,最前面 K 个元素就是目前最大的 K 个元素,以后每来一个新元素,都先找数组中的最小值,将新元素与最小值相比,如果小于最小值,则什么都不变,如果大于最小值,则将最小值替换为新元素。这样一来,数组中维护的永远是最大的 K 个元素,不管数据源有多少,需要的内存开销都是固定的,就是长度为 K 的数组。不过,每来一个元素,都需要找到最小值,进行 K 次比较,是否有办法能减少比较次数呢?
当然,这时候堆就要登场了,我们使用最小堆维护这 K 个元素,每次来新的元素,只需要和根节点比较,小于等于根节点,不需要变化,否则用新元素替换根节点,然后 siftDown 调整堆即可。此时的时间复杂度为 O(nlogK) ,相比上述两种方法,效率大大提升,且空间复杂度也大大降低。
Top K 问题代码:
- public class TopK<E extends Comparable<E>> {
- private PriorityQueue<E> p;
- private int k;
- public TopK(int k) {
- this.k = k;
- this.p = new PriorityQueue<>(k);
- }
- public void addAll(Collection<? extends E> c) {
- for (E e : c) {
- add(e);
- }
- }
- public void add(E e) {
- // 未满k个时,直接添加
- if (p.size() < k) {
- p.add(e);
- return;
- }
- E head = p.peek();
- if (head != null && head.compareTo(e) >= 0) {
- // 小于等于TopK中的最小值,不用变
- return;
- }
- // 否则,新元素替换原来的最小值
- p.poll();
- p.add(e);
- }
- /**
- * 获取当前的最大的K个元素
- *
- * @param a 返回类型的空数组
- * @param <T>
- * @return TopK以数组形式
- */
- public E[] toArray(E[] a) {
- return p.toArray(a);
- }
- /**
- * 获取第K个最大的元素
- *
- * @return 第K个最大的元素
- */
- public E getKth() {
- return p.peek();
- }
- public static void main(String[] args) {
- TopK<Integer> top5 = new TopK<>(5);
- top5.addAll(Arrays.asList(88, 1, 5, 7, 28, 12, 3, 22, 20, 70));
- System.out.println("top5:" + Arrays.toString(top5.toArray(new Integer[0])));
- System.out.println("5th:" + top5.getKth());
- }
- }
这里我们直接利用 JDK 自带的由最小堆实现的优先级队列 PriorityQueue 。
依此思路,可以实现求前 K 个最小元素,只需要在实例化 PriorityQueue 时传入一个反向比较器参数,然后更改 add 方法的逻辑。
中位数
堆也可以用于求解中位数,数据量可能很大且源源不断到来。
注意:如果元素个数是偶数,那么我们假定中位数取任意一个都可以。
有了上面的例子,这里就很好理解了。我们使用两个堆,一个最大堆,一个最小堆,步骤如下:
- 添加的第一个元素作为中位数 m,最大堆维护 <= m 的元素,最小堆维护 >= m 的元素,两个堆都不包含 m。
- 当添加第二个元素 e 时,将 e 与 m 比较,若 e <= m,则将其加入到最大堆中,否则加入到最小堆中。
- 如果出现最小堆和最大堆的元素个数相差 >= 2,则将 m 加入元素个数少的堆中,然后让元素个数多的堆将根节点移除并赋值给 m。
- 以此类推不断更新。
假设有数组 [20, 30, 40, 50, 2, 4, 3, 5, 7, 8, 10] 。
下图展示了整个操作的过程:
求解中位数的代码:
- public class Median<E extends Comparable<E>> {
- /**
- * 最小堆
- */
- private PriorityQueue<E> minP;
- /**
- * 最大堆
- */
- private PriorityQueue<E> maxP;
- /**
- * 当前中位数
- */
- private E m;
- public Median() {
- this.minP = new PriorityQueue<>();
- this.maxP = new PriorityQueue<>(11, Collections.reverseOrder());
- }
- private int compare(E e, E m) {
- return e.compareTo(m);
- }
- public void addAll(Collection<? extends E> c) {
- for (E e : c) {
- add(e);
- }
- }
- public void add(E e) {
- // 第一个元素
- if (m == null) {
- m = e;
- return;
- }
- if (compare(e, m) <= 0) {
- // 小于等于中值,加入最大堆
- maxP.add(e);
- } else {
- // 大于中值,加入最大堆
- minP.add(e);
- }
- if (minP.size() - maxP.size() >= 2) {
- // 最小堆元素个数多,即大于中值的数多
- // 将 m 加入到最大堆中,然后将最小堆中的根移除赋给 m
- maxP.add(m);
- m = minP.poll();
- } else if (maxP.size() - minP.size() >= 2) {
- minP.add(m);
- m = maxP.poll();
- }
- }
- public E getMedian() {
- return m;
- }
- public static void main(String[] args) {
- Median<Integer> median = new Median<>();
- median.addAll(Arrays.asList(20, 30, 40, 50, 2, 4, 3, 5, 7, 8, 10));
- System.out.println(median.getMedian());
- }
- }