初学者在学习C语言的过程中,遇到“递归”的概念时,常常会感到迷惑。坦诚地说,“递归”在编程语言中的确是一个比较难理解的概念,而且“递归”能解决的问题,一般循环语句也能解决,从某种程度上来说,C语言中的“递归”和循环语句是等价的,既然如此,为什么C语言不“丢弃”难以理解的“递归”呢?
C语言为什么不丢弃“递归”?
其实,“递归”究竟是否难以理解取决于程序员看问题的角度。应该明白,C语言程序是为人们现实生活需求服务的,在我看来,如果脱离了实际问题,仅从编程语言的角度来看问题,“递归”的确比较难理解,相反,如果结合要实际解决的问题,有时“递归”反而更加清晰易懂。请看下面这段C语言代码示例:
- int factorial(int n){ if(0 == n) return 1; else return n*factorial(n-1);}
factorial() 函数是一个典型的递归函数,虽然它的代码很简单,但如果仅从编程语言的角度来理解这个函数,的确有些难度——当 n!=0 时,函数似乎永远在嵌套自己,虽说粗暴的逐步分析能够得到函数的输出,但是稍不留神就会出错。
现在换个角度考虑 factorial() 函数,尝试从该函数要解决的“实际需求”上分析,应该不难得到 factorial() 函数其实在说:
- 如果 n 等于 0,那么 f(n) 等于 1,也即 f(0) 等于 1
- 如果 n 不等于 0,那么 f(n) 等于 n*f(n-1)
将这两句话转换为数学语言,也就是:
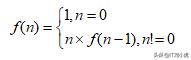
factorial()函数的数学描述
如果限定 n 为不小于 0 的整数,那么这显然就是数学中整数阶乘的定义,也即 factorial(n) 函数的输出为 n!。可以看出,递归函数 factorial() 其实就是直白的使用C语言“描述”了 n! 的数学定义,因此从这个角度来看,“递归”似乎又不是那么难理解。
当然了,使用C语言的循环语句编写程序计算 n! 也是可以的,读者可自行编写,应该能够发现,循环语句计算 n! 更像是使用“笨方法”一点点的计算,它与“递归”实现从设计思维上来看是不同的。
因此,从上面这个例子可以看出,C语言中的“递归”倒不像是一种语法,而是一种“编程思维”,所以“丢弃”便无从说起了。当然了,严格来说,C语言对“递归”也是做了一定的支持,至少递归函数就属于C语言的一种语法,这其实与C语言的基本设计思想有关:C语言从诞生至今,有一个特点是始终坚持的——尽可能的保持简洁,给程序员比较大的自由。所以,既然“递归”思维是一个不错的思维,C语言当然要提供递归函数予以支持了。
再来看一个例子
为了加深对递归的理解,这里再举一个例子,请看下面这段C语言代码:
- #include void test(int left, int right) { if (left >= right) return; int mid = (left+right) /2; printf("before: %d %d %d\n", left, mid, right); test(left, mid); test(mid+1, right); printf("after : %d %d %d\n", left, mid, right);} int main() { test(0, 5); return 0;}
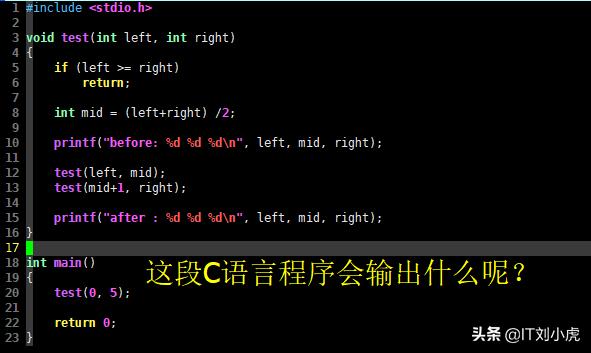
test() 函数的C语言代码
test() 函数显然是一个递归函数,它的代码也比较简单,只不过在其内部递归调用了两次,稍稍复杂了一些。接下来,我们将分别从编程语言角度,和实际需求角度分别分析 test() 函数的功能。
首先,从编程语言角度来看,显然 test() 函数会被多次调用,为了便于讨论,每发生一次 test() 函数调用,我们就在函数名后加一个后缀“_xx”。
test() 函数首次被调用是在 main() 函数中,进入 test() 函数后,程序会先递归调用 test(left, mid); 行此时可写作:
- test_0(0, 5):输出“before:0 2 5”,调用 test_1(0, 2)
- test_1(0, 2):输出“before:0 1 2”,调用 test_2(0, 1)
- test_2(0, 1):输出“before:0 0 1”,调用 test_3(0, 0)
- test_3(0, 0):因为 0>=0,所以直接返回 test_2(0, 1)
此时应注意,test_0~3() 都是在执行到“test(left, mid)”时发生递归调用的,因此它们将返回到“test(mid+1, right)”处。
返回到 test_2(0, 1) 时,left=0, right=1, mid=0,因此 test(mid+1, right) 会直接返回,输出“after:0 0 1”;接着返回 test_1(0, 2),同理,输出“after:0 1 2”;接着返回 test_0(0, 5) 的 test(mid+1, right); 行,此时 left=0, right=5, mid=2,接下来的过程将如下进行:
- test_4(3, 5):输出“before:3 4 5”,调用 test_5(3, 4)
- test_5(3, 4):输出“before:3 3 4”,调用 test_6(3, 3)
- test_6(3, 3):因为 3>=3,所以直接返回 test_5(3, 4)
此时应注意 test4~6() 是在执行 “test(mid+1, right)”时发生递归调用的,因此它们将返回到“printf("after:...”处。
函数返回到 test_5(3, 4) 后,此时 left=3, right=4, mid=3,因此 输出“after:3 3 4”,并返回 test_4(3, 5),输出“after:3 4 5”,并返回 test_0(0, 5),输出“after:0 2 5”。整理一下,得到上述C语言程序的输出如下:
- before: 0 2 5before: 0 1 2before: 0 0 1after : 0 0 1after : 0 1 2before: 3 4 5before: 3 3 4after : 3 3 4after : 3 4 5after : 0 2 5
可见,从编程语言角度来分析递归函数,的确是一件比较吃力的事情,若是输入给 test(0, 105) 函数的参数更宽一些,基本上可以认为是不可分析的。现在我们尝试从实际需求角度理解递归函数 test() 的功能,应该能够轻易得到以下信息:
- 当输入的 left 不小于 right 时,函数直接返回
- 否则 test() 函数将打印 left 与 right 以及它俩的平均整数值 mid
- 接着,令 right=mid,并重复上述过程;令 left=mid+1,并重复上述过程
- 打印在这之后的 left,mid,right
稍加理解,基本应该能明白 test() 函数的功能了:mid 是 left 和 right 的二分中间值,因此 test(left, mid) 可以看作是二分之后的左半部分,test(mid+1, right) 则可以看作是二分之后的右半部分,因此 test() 函数的作用其实就是在不停的二分 left~right 区间,一直到不能继续二分为止(left>=right),这一过程是逐步递归的,因此 test() 函数也会逐步输出二分的结果。以分析“after:...”输出为例,test(0, 5) 会依次输出:
- 0 0 10 1 23 3 43 4 50 2 5
这与从编程语言角度分析的结果是一致的。理解这一点后,现在我们引入应用实例,假定有一个数组 {3,2,5,1,4},调用 test(0,5) 逐步二分该数组,过程应该如下图所示:
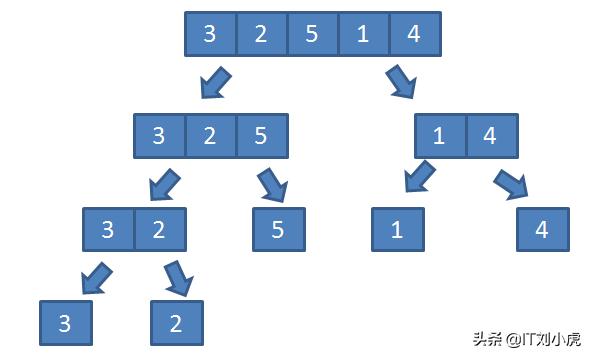
二分数组过程
至此,我们便从实际需求角度分析了递归函数,可见,理解递归函数其实就是理解其设计,站在更高处从大局出发理解其含义的。
小结
“递归”不能算是C语言中的语法,它更像是一种思想,因此“C语言为什么不丢弃“递归””这种说法是没有意义的。本文还通过两个实例,从编程语言和实际应用两个角度讨论了如何分析C语言中的递归函数,可见,递归有时的确能够简洁的解决问题。不过不得不承认,递归的确是一个较难理解的概念,而且递归函数也比较难以调试,消耗栈空间巨大,因此在实际的C语言程序开发中,除非递归能够带来极大的便利,否则不建议使用递归,而是尽量尝试使用循环解决问题。
































