大家好,我是鸭血粉丝,拼着头发掉光的风险给大家总结了这篇文章,我愿拿我明年的今天还是单身来祝愿你们能学会~
所谓二叉查找树,就是按照二分进行查找,每次查询只需要选择其中一个子树就进行查找,从而减少查找次数,提升查询效率!
一、介绍
在前面的文章中,我们对树这种数据结构做了一些基本介绍,今天我们继续来聊聊一种非常常用的动态查找树: 二叉查找树。
二叉查找树,英文全称:Binary Search Tree,简称:BST,它是计算机科学中最早投入实际使用的一种树形结构,特性如下:
- 若左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不为空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 它的左、右子树也分别为二叉查找树;
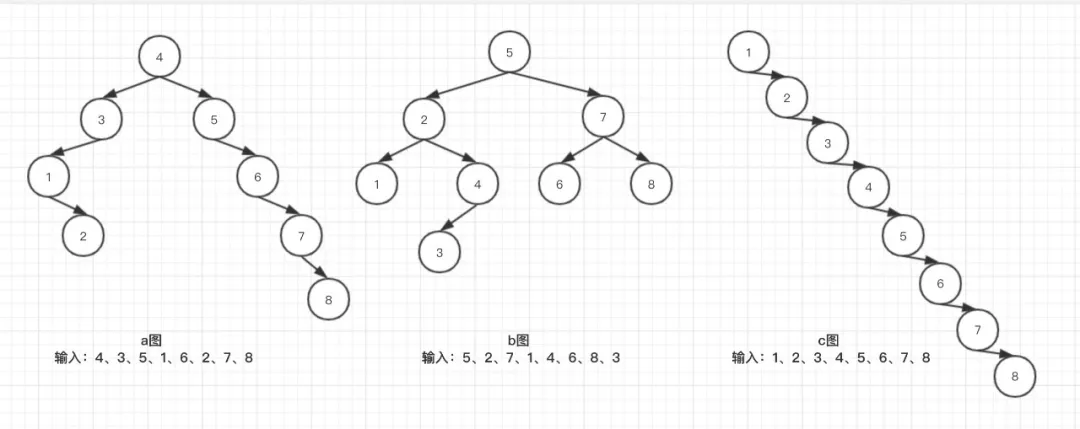
特性定义比较粗放,所以在树形形态结构上,有着多样,例如下图:
上图 a、b、c 三个图,都满足以上特性,也被称为二叉查找树,虽然通过中序遍历可以得到一个有效的数组:[1、2、3、4、5、6、7、8],但是就查找效率来说,有着一定的差别,例如查询目标为8的内容,从根目录开始查询,结构如下:
- a图,需要5次;
- b图,需要3次;
- c图,需要8次;
由此可见,不同的形状,所需查找的次数是不一样的,关于这一点,后面我们在介绍平衡二叉查找树、红黑树这种数据结构的时候,会进行详细介绍。
虽然二叉查找树,在不同的形状下,查找效率不一样,但是它是学习其他树形结构的基础,了解了二叉查找树的算法,相信再了解其他二叉树结构会轻松很多。
二、算法思路
2.1、 新增
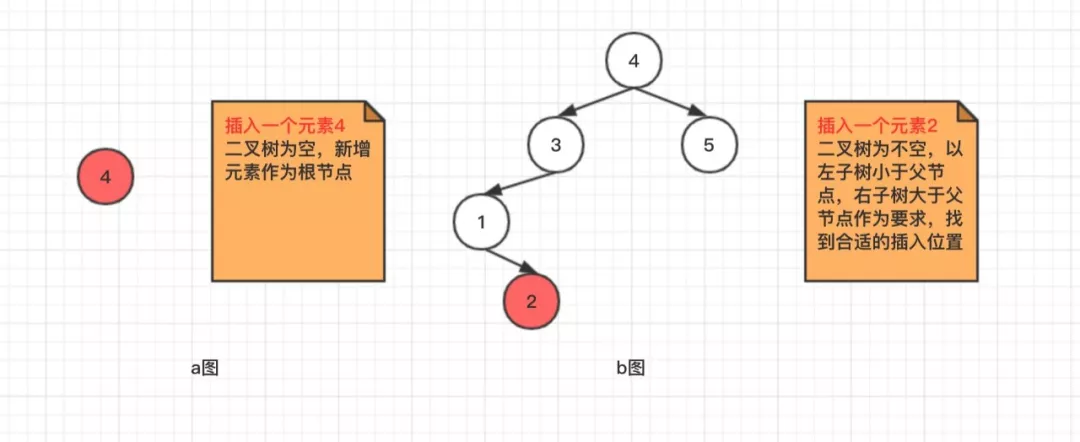
新增元素表示向二叉树中添加元素,比较简单。如果二叉树为空,默认第一个元素就是根节点,如果二叉树不为空,就以上面提到的特点为判断条件,进行左、右节点的添加。
2.2、 查找
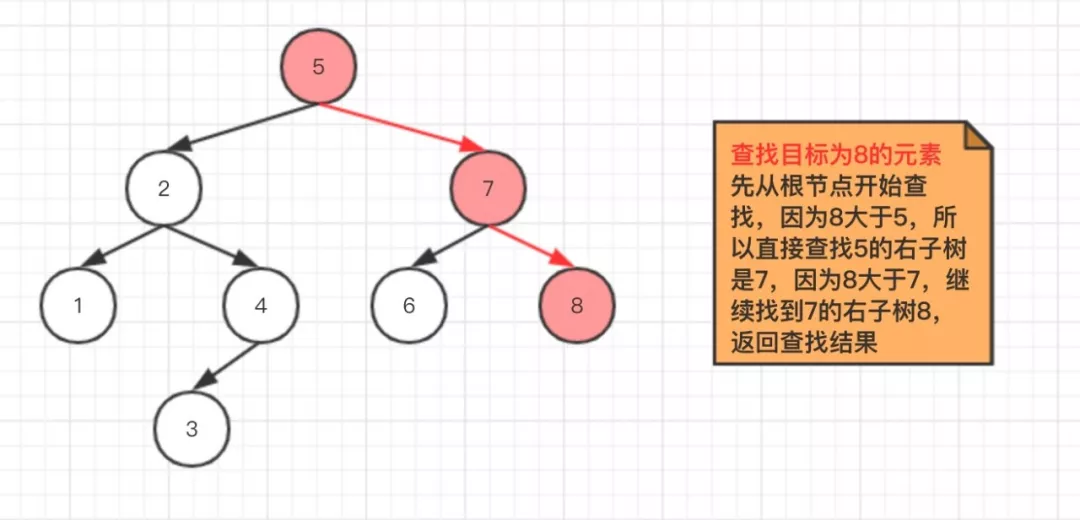
查找元素表示从根节点开始查找元素,如果根节点为空,就直接返回空值,如果不为空,通过以左子树小于父节点,右子树大于父节点的特性为依据进行判断,然后以递归方式进行查找元素,直到找到目标的元素为止。
2.3、 删除
删除元素表示从二叉树中移除要删除的元素,逻辑稍微复杂一些。同样,先要判断根节点是否为空,如果为空,直接返回,如果不为空,分情况考虑。
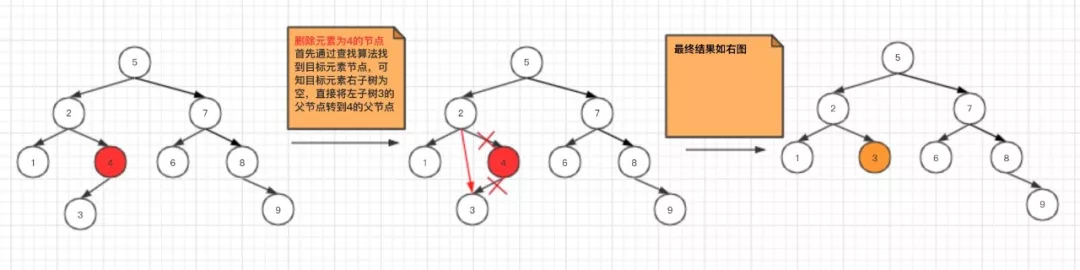
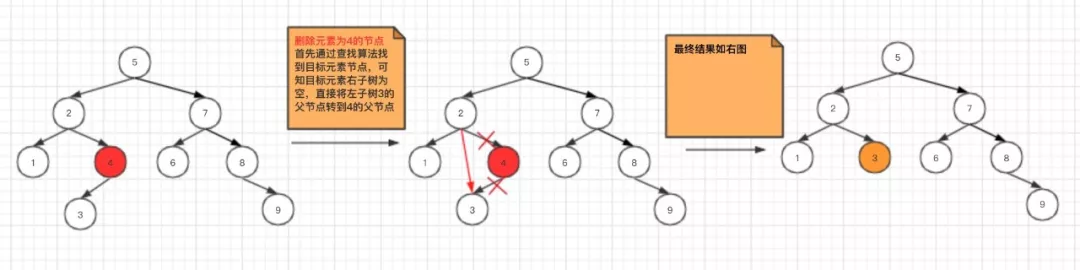
被删除的节点,右子树为空
这种场景,只需要将被删除元素的左子树的父节点移动到被删除元素的父节点,然后将被删除元素移除即可。
- 被删除的节点,左子树为空
这种场景,与上面类似,只需要将被删除元素的右子树的父节点移动到被删除元素的父节点,然后将被删除元素移除即可。
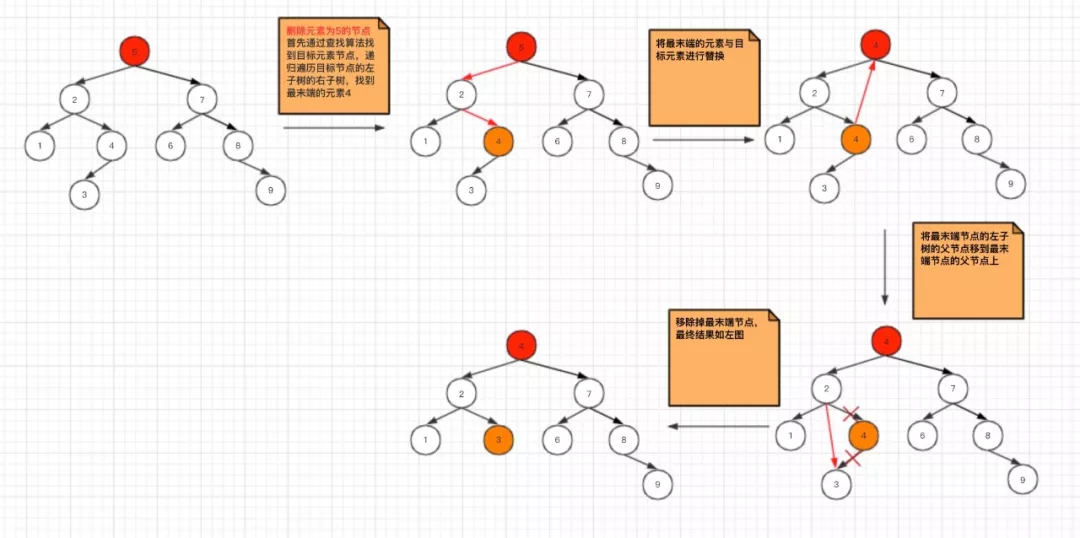
- 被删除的节点,左、右子树不为空
这种场景,稍微复杂一点,先定位到要删除的目标元素,根据左子节点内容一定小于当前节点内容特点,找到目标元素的左子树,通过递归遍历找到目标元素的左子树的右子树,找到最末端的元素之后,进行与目标元素进行替换,最后移除最末端元素。
2.4、 遍历
二叉树的遍历方式,分两类:
- 层次遍历,从根节点开始;
- 深度遍历,又分为前序、中序、后序遍历三种方式;
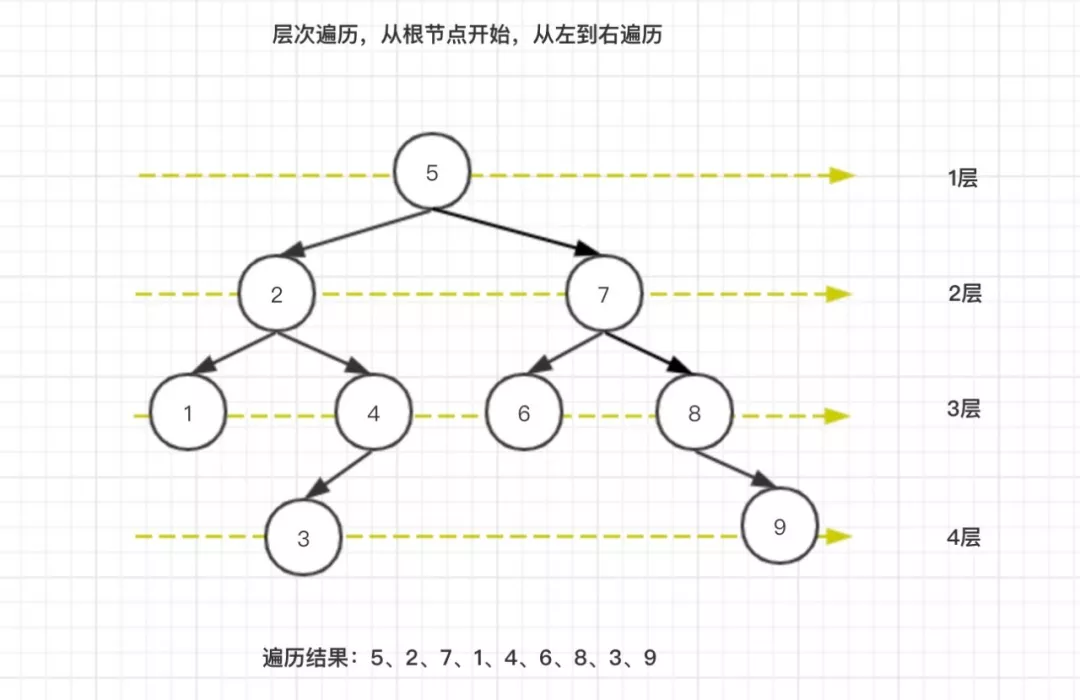
2.4.1、层次遍历
层次遍历,算法思路比较简单,从根节点开始,分层从左到右进行遍历元素。
2.4.2、深度遍历
深度遍历,在遍历起始位置上又分三种,分别是前序遍历、中序遍历、后序遍历,每种遍历方式输出的结果不一样。
- 前序遍历:从树根开始 -> 左子树 -> 右子树
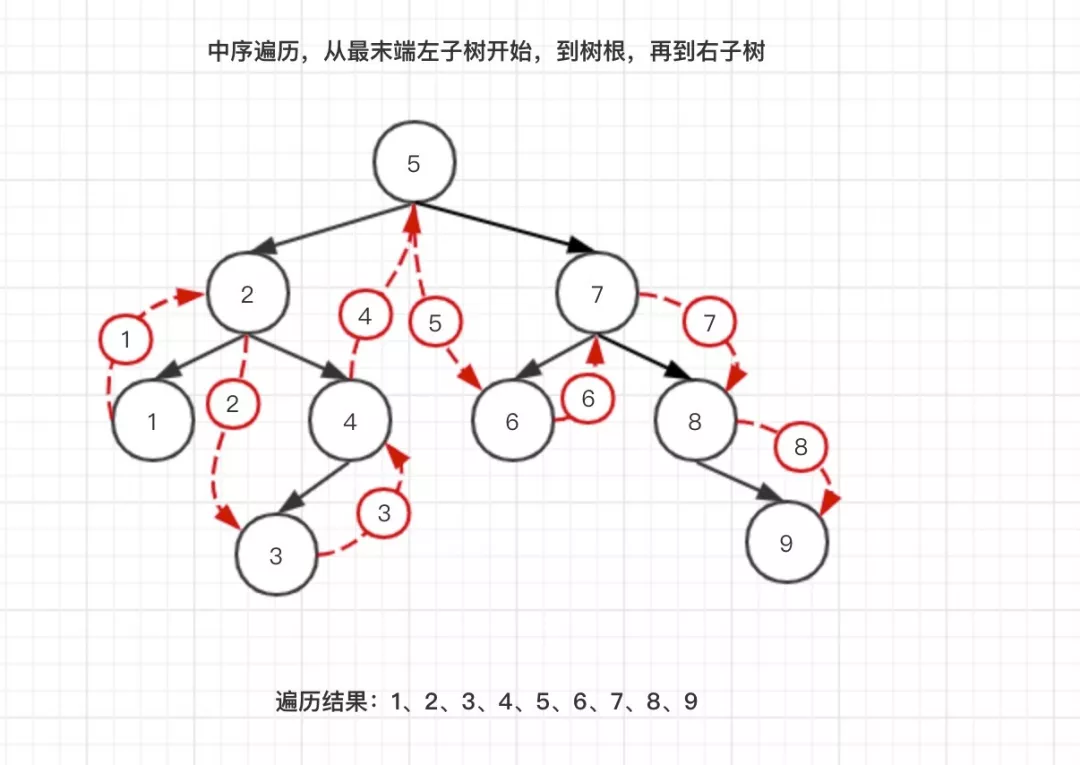
- 中序遍历:从最末端左子树开始 -> 树根 -> 右子树
- 后序遍历:从最末端左子树 -> 右子树 -> 最后到树根
尽管二叉树在遍历方式上有多种,但是只要我们掌握了其中的思路原理,再去实现起来,就会轻松很多。
三、代码实践
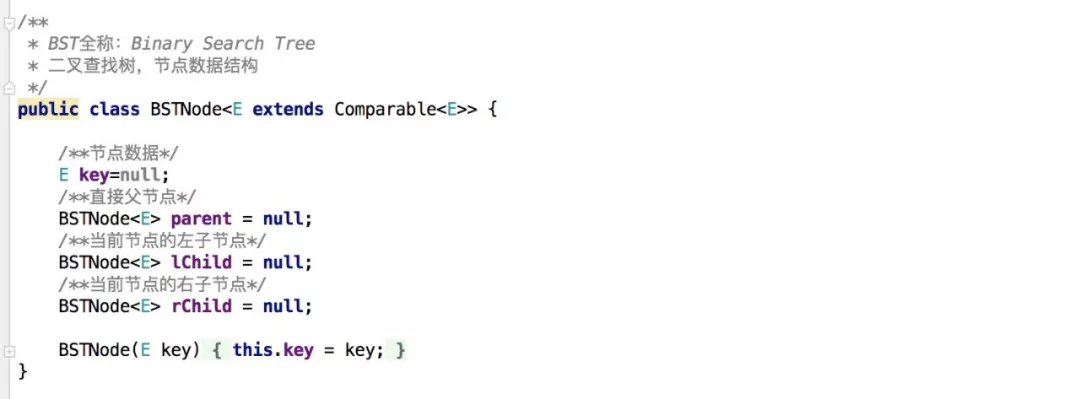
首先创建一个实体数据结构BSTNode,内容如下:
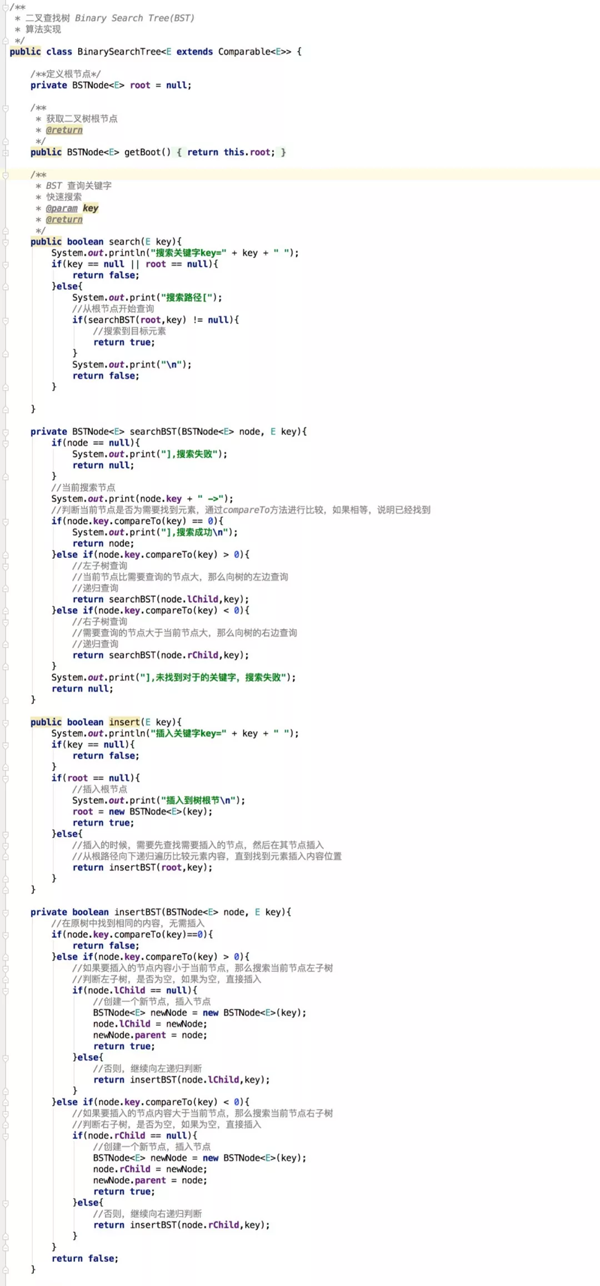
然后,创建一个二叉查找树操作类BinarySearchTree,内容如下:
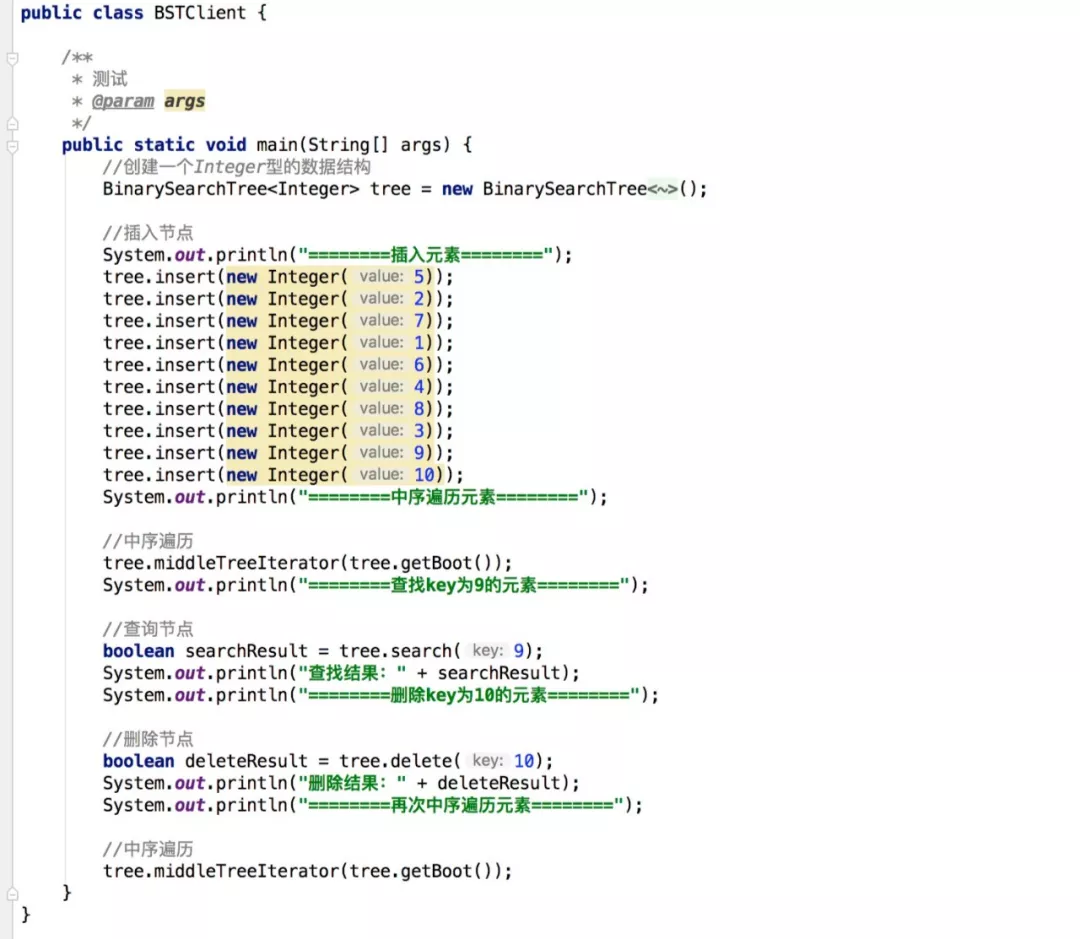
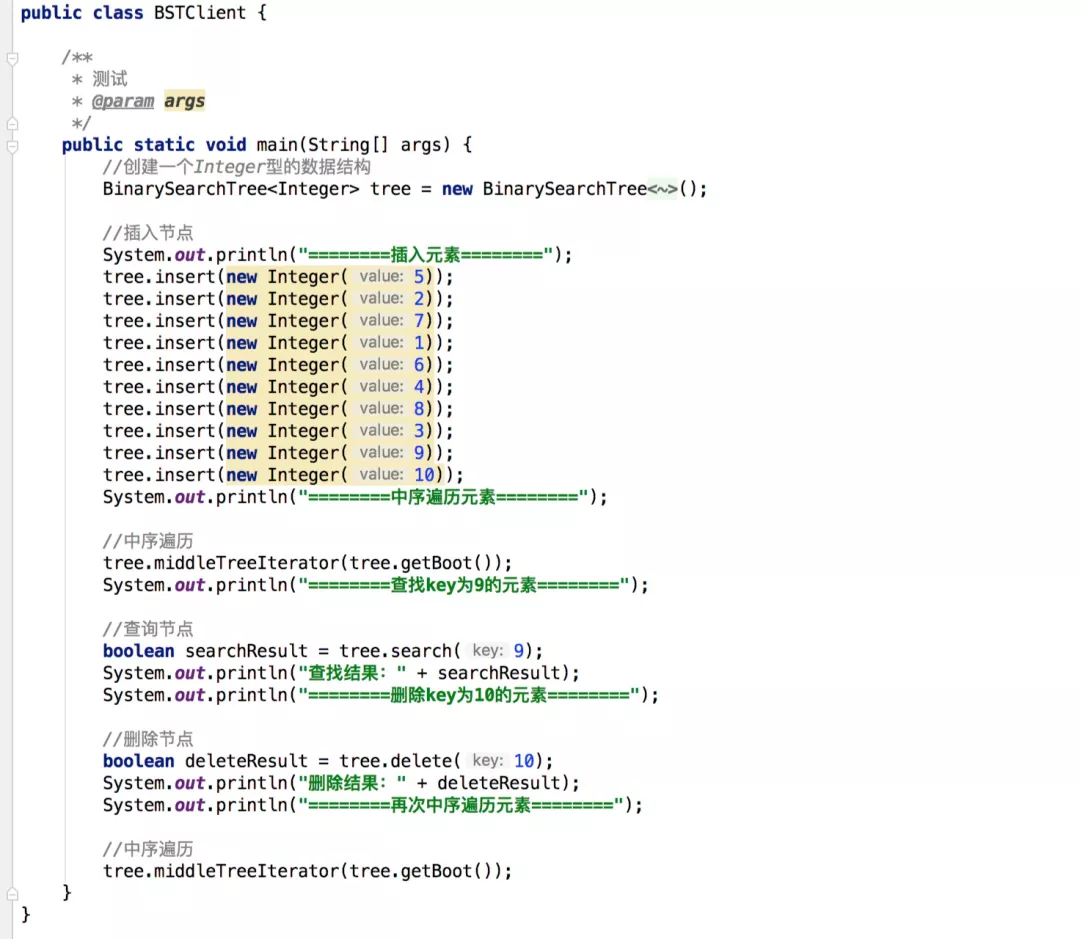
最后,我们来测试一下,代码内容如下:
输出结果:
- ========插入元素========
- 插入关键字key=5
- 插入到树根节
- 插入关键字key=2
- 插入关键字key=7
- 插入关键字key=1
- 插入关键字key=6
- 插入关键字key=4
- 插入关键字key=8
- 插入关键字key=3
- 插入关键字key=9
- 插入关键字key=10
- ========中序遍历元素========
- key:1
- key:2
- key:3
- key:4
- key:5
- key:6
- key:7
- key:8
- key:9
- key:10
- ========查找key为9的元素========
- 搜索关键字key=9
- 搜索路径[5 ->7 ->8 ->9 ->],搜索成功
- 查找结果:true
- ========删除key为10的元素========
- 删除关键字key=10
- 开始搜索目标元素[5 ->7 ->8 ->9 ->10 ->],搜索成功
- 删除结果:true
- ========再次中序遍历元素========
- key:1
- key:2
- key:3
- key:4
- key:5
- key:6
- key:7
- key:8
- key:9
四、总结
二叉查找树,作为树类型中一种非常重要的数据结构,有着非常广泛的应用,但是二叉查找树具有很高的灵活性,不同的插入顺序,可能造成树的形态差异比较大,如开文介绍的图c,在某些情况下会变成一个长链表,此时的查询效率会大大降低,如何解决这个问题呢,平衡二叉树就要派上用场了,会在后面的文章进行介绍!
(第一句话是开玩笑,呸呸呸,情人节快乐)