用 JavaScript 学习算法复杂度-javascript 算法

在本文中，我们将探讨 “二次方” 和 “n log(n)” 等术语在算法中的含义。

在后面的例子中，我将引用这两个数组，一个包含 5 个元素，另一个包含 50 个元素。我还会用到 JavaScript 中方便的 performance API 来衡量执行时间的差异。

const smArr = [5, 3, 2, 35, 2]; 
 
const bigArr = [5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2];

什么是 Big O 符号?

Big O 表示法是用来表示随着数据集的增加，计算任务难度总体增长的一种方式。尽管还有其他表示法，但通常 big O 表示法是最常用的，因为它着眼于最坏的情况，更容易量化和考虑。最坏的情况意味着完成任务需要最多的操作次数;如果你在一秒钟内就能恢复打乱魔方，那么你只拧了一圈的话，不能说自己是做得最好的。

当你进一步了解算法时，就会发现这非常有用，因为在理解这种关系的同时去编写代码，就能知道时间都花在了什么地方。

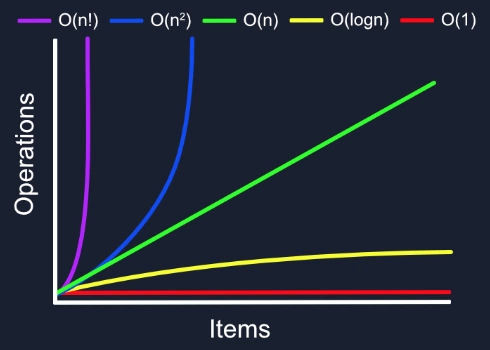
当你了解更多有关 Big O 表示法的信息时，可能会看到下图中不同的变化。我们希望将复杂度保持在尽可能低的水平，最好避免超过 O(n)。

O(1)

这是理想的情况，无论有多少个项目，不管是一个还是一百万个，完成的时间量都将保持不变。执行单个操作的大多数操作都是 O(1)。把数据写到数组、在特定索引处获取项目、添加子元素等都将会花费相同的时间量，这与数组的长度无关。

const a1 = performance.now(); 
smArr.push(27); 
const a2 = performance.now(); 
console.log(`Time: ${a2 - a1}`); // Less than 1 Millisecond 
 
 
const b1 = performance.now(); 
bigArr.push(27); 
const b2 = performance.now(); 
console.log(`Time: ${b2 - b1}`); // Less than 1 Millisecond

O(n)

在默认情况下，所有的循环都是线性增长的，因为数据的大小和完成的时间之间存在一对一的关系。所以如果你有 1,000 个数组项，将会花费的 1,000 倍时间。

const a1 = performance.now(); 
smArr.forEach(item => console.log(item)); 
const a2 = performance.now(); 
console.log(`Time: ${a2 - a1}`); // 3 Milliseconds 
 
const b1 = performance.now(); 
bigArr.forEach(item => console.log(item)); 
const b2 = performance.now(); 
console.log(`Time: ${b2 - b1}`); // 13 Milliseconds

O(n^2)

指数增长是一个陷阱，我们都掉进去过。你是否需要为数组中的每个项目找到匹配对?将循环放入循环中是一种很好的方式，可以把 1000 个项目的数组变成一百万个操作搜索，这将会使你的浏览器失去响应。与使用双重嵌套循环进行一百万次操作相比，最好在两个单独的循环中进行 2,000 次操作。

const a1 = performance.now(); 
smArr.forEach(() => { 
    arr2.forEach(item => console.log(item)); 
}); 
const a2 = performance.now(); 
console.log(`Time: ${a2 - a1}`); // 8 Milliseconds 
 
 
const b1 = performance.now(); 
bigArr.forEach(() => { 
    arr2.forEach(item => console.log(item)); 
}); 
const b2 = performance.now(); 
console.log(`Time: ${b2 - b1}`); // 307 Milliseconds

O(log n)

我认为关于对数增长比较好的比喻，是想象在字典中查找像 “notation” 之类的单词。你不会在一个词条一个词条的去进行搜索，而是先找到 “N” 这一部分，然后是 “OPQ” 这一页，然后按字母顺序搜索列表直到找到匹配项。

通过这种“分而治之”的方法，找到某些内容的时间仍然会因字典的大小而改变，但远不及 O(n) 。因为它会在不查看大部分数据的情况下逐步搜索更具体的部分，所以搜索一千个项目可能需要少于 10 个操作，而一百万个项目可能需要少于 20 个操作，这使你的效率最大化。

在这个例子中，我们可以做一个简单的快速排序。

const sort = arr => { 
  if (arr.length < 2) return arr; 
 
  let pivot = arr[0]; 
  let left = []; 
  let right = []; 
 
  for (let i = 1, total = arr.length; i < total; i++) { 
    if (arr[i] < pivot) left.push(arr[i]); 
    else right.push(arr[i]); 
  }; 
  return [ 
    ...sort(left), 
    pivot, 
    ...sort(right) 
  ]; 
}; 
sort(smArr); // 0 Milliseconds 
sort(bigArr); // 1 Millisecond

O(n!)

最糟糕的一种可能性是析因增长。最经典的例子就是旅行的推销员问题。如果你要在很多距离不同的城市之间旅行，如何找到在所有城市之间返回起点的最短路线?暴力方法将是检查每个城市之间所有可能的路线距离，这是一个阶乘并且很快就会失控。

由于这个问题很快会变得非常复杂，因此我们将通过简短的递归函数演示这种复杂性。这个函数会将一个数字去乘以函数自己，然后将数字减去1。阶乘中的每个数字都会这样计算，直到为 0，并且每个递归层都会把其乘积添加到原始数字中。

阶乘只是从 1 开始直至该数字的乘积。那么 6!是 1x2x3x4x5x6 = 720。

const factorial = n => { 
  let num = n; 
 
  if (n === 0) return 1 
  for (let i = 0; i < n; i++) { 
    num = n * factorial(n - 1); 
  }; 
 
  return num; 
}; 
factorial(1); // 2 Milliseconds 
factorial(5); // 3 Milliseconds 
factorial(10); // 85 Milliseconds 
factorial(12); //  11,942 Milliseconds

我原本打算显示 factorial(15)，但是 12 以上的值都太多，并且使页面崩溃了，这也证明了为什么需要避免这种情况。

结束语

我们需要编写高性能的代码似乎是一个不争得事实，但是我敢肯定，几乎每个开发人员都创建过至少两重甚至三重嵌套循环，因为“它确实有效”。Big O 表示法在表达和考虑复杂性方面是非常必要的，这是我们从未有过的方式。