导读
LDA是文档分类上的经典算法,如何应用到推荐系统上,大家可以看看。
Latent Dirichlet Allocation(LDA)是一种无监督发现语料库底层主题的主题建模算法。它已被广泛应用于各种领域,特别是在自然语言处理和推荐系统中。这篇博文将带你从LDA的概况介绍到详细的技术说明,最后我们将讨论LDA在推荐系统上的应用!
概要介绍
LDA是语料库/文档的生成概率模型。它基于“词袋”假设,即词语和文档是可互换的。也就是说,忽略了文档中文字的顺序,或者忽略了文档的顺序。其基本思想是每个文档都是由不同的主题组合而成,而每个主题的是通过单词的分布来描述。
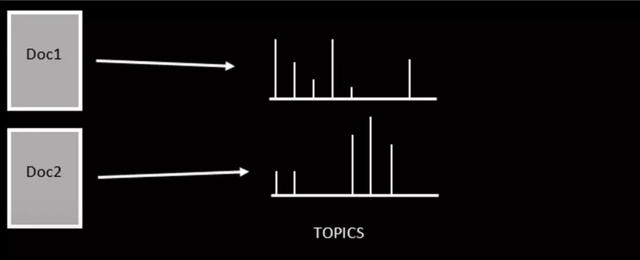
每个文档都由一个主题分布组成
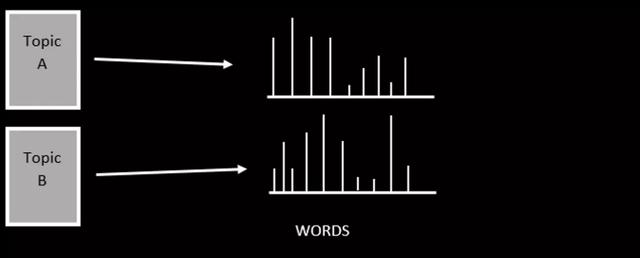
每个主题都用单词的分布来表示
LDA假设单个文档的生成都是通过从每个文档中抽取主题,然后从每个抽取的主题中抽取单词来生成的。为了获得单词和主题的适当分布,我们可以使用Gibbs Sampling、Maximum a Posteriori (MAP)或expect Maximization (EM)来训练LDA。
Plate表示法
为了更深入一点,让我们讨论一下LDA的符号表示法。在贝叶斯推理中,Plate表示法是一种图形化的表示随机变量抽样的重复过程的方法。每个plate可以看作是一个“循环”,其中plate右下角的变量表示循环的迭代次数。下面是LDA的Plate表示法。
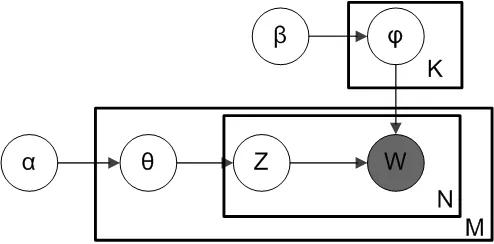
LDA plate 表示法
在上面的图中有两个组件。上面的plate,有K个主题,这些主题的词的狄利克雷分布由超参数β控制。同样,下面的表格描述了有M个文档,每个文档包含N个单词。灰色的圆圈w是观察到的单词,圆圈代表不同的潜在变量。z指的是与w相关联的主题,θ是文档主题的狄利克雷分布,由另一个超参数⍺控制。
生成过程
现在我们大致了解了如何通过plate表示法来生成文档。让我们用数学来表示它。
- 从狄利克雷分布(θ_i ~ Dir(⍺),i从1到M)中采样θ
- 从另一个狄利克雷分布(φ_k ~ Dir(β) k从1到K)中采样φ
- 从z_ij ~ Multinomial(θ_i) 采样,从w_ij ~ Multinomial(φ_z_ij) 中采样,i从1到M,j从1到N
以《纽约时报》为例。首先,对于每个新闻文章,我们对整个文档的主题分布θ_i_进行采样。对每个主题中词的分布φ_k_进行采样。然后,对于每个文档中的词j,我们从给定的主题分布Multinomial(θ_i)中得到一个主题z_ij,然后从给定的词的分布Multinomial(φ_z_ij)中的到w_ij,并基于w_ij采样得到一个单词。这个过程通过下面的图来表示。

生成过程的可视化
狄利克雷分布
我们一直把狄利克雷作为黑盒子,却没有给出任何解释。让我们简要地讨论一下狄利克雷分布背后的直觉。一个k维狄利克雷分布由一个k维参数向量控制。下面我们展示一个狄利克雷分布的三维例子。基本思想是,alpha值越大,分布被推到中心的概率越大。这种分布使得确定与主题/文档相关联的单词/主题的部分具有很高的灵活性,因为一些主题/文档可能与一组很大的单词/主题相关联,而其他的可能不相关联。
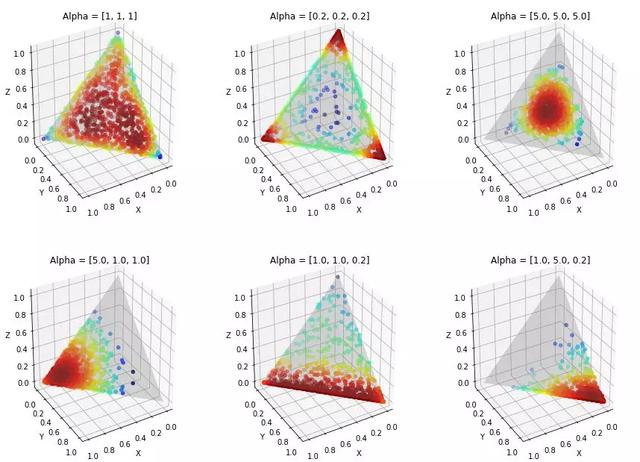
狄利克雷分布
学习
学习LDA模型的问题称为“推理”问题。给定观测变量w,以及超参数⍺和β,我们如何估计潜变量的后验概率。
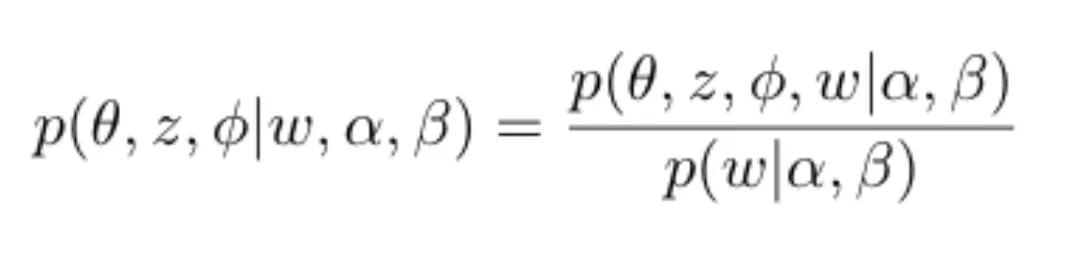
然而,分母中计算的积分在计算上是很麻烦的。
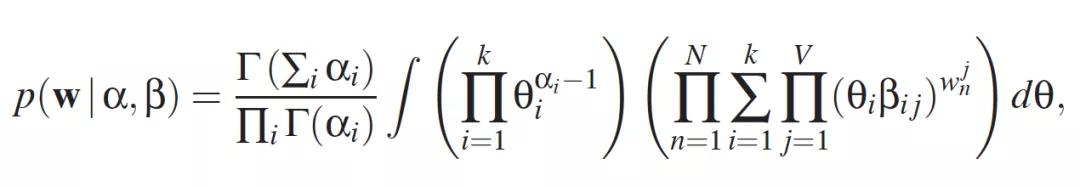
因此,必须使用近似推理。常用的方法是吉布斯抽样和变分推论。在这篇文章中,我们将重点讨论前者。
吉布斯抽样
利用吉布斯采样,我们可以避免直接计算棘手的积分。基本的想法是,我们想从p (w |⍺,β)中采样来估计这个分布,但我们不能直接这样做。相反,Gibbs抽样允许我们迭代地计算一个潜在变量的后验值,同时固定所有其他变量。通过这种方式,我们可以获得后验分布p(θ, z, φ| w, ⍺, β)。
对于每次迭代,我们交替采样w,⍺,β,并固定所有其他变量。算法如下面的伪代码所示:
For i from 1 to MaxIter:
- Sample θ_i} ~p(θz= z_{i-1, φ = φ_{i-1}w, ⍺, β)
- Sample z_i} ~p(zθ =θ_{i, φ = φ_{i-1}w, ⍺, β)
- Sample φ_i} ~p(φθ = θ_{i, z= z_{i}w, ⍺, β)
由于来自早期迭代的样本不稳定,我们将丢弃样本的第一个B次迭代,称为“老化”。
LDA在推荐系统上的应用
LDA通常用于两种情况下的推荐系统:
- 协同过滤(CF)
- 基于内容的推荐
协同过滤
当LDA应用于基于物品的CF时,物品和用户类似于我们一直在讨论的文档和单词(基于用户的CF正好相反)。换句话说,每个物品都与用户组(主题)上的分布相关联,每个用户组都是用户的分布。使用LDA,我们可以发现用户和物品之间的隐藏关系。
基于内容的推荐
第二个应用是基于内容的推荐,非常简单。我们不只是利用普通的TF-IDF来提取每个物品的文本数据的特征向量,而且还通过LDA来对这些文本数据的主题进行建模。下面提供了用于训练LDA和推断给定文档主题的示例代码。
- from gensim.test.utils import common_textsfrom gensim.corpora.dictionary import Dictionaryfrom gensim.models import LdaModel# Create a corpus from a list of textscommon_dictionary = Dictionary(common_texts)common_corpus = [common_dictionary.doc2bow(text) for text in common_texts]# Train the model on the corpus.lda = LdaModel(common_corpus, num_topics=10)
训练LDA
- # infer the topic distribution of the second corpus.lda[common_corpus[1]]'''output[(0, 0.014287902), (1, 0.014287437), (2, 0.014287902), (3, 0.014285716), (4, 0.014285716), (5, 0.014285714), (6, 0.014285716), (7, 0.014285716), (8, 0.014289378), (9, 0.87141883)]'''
推断主题的分布向量
总结
在这篇博文中,我们讨论了LDA从高层到详细的数学解释。另外,我们还讨论了LDA在推荐系统上的应用,并提供了如何使用的示例代码。我希望这篇文章对你有帮助,下次再见