如何使用 Julia 语言实现「同态加密+机器学习」？

[[285696]]

 最近，「区块链」、「联邦学习」等概念受到了空前的关注。而在这些概念背后，少不了一项技术的影子——「同态加密」。本文介绍了使用 Julia 语言进行基于同态加密数据机器学习的全过程，对于入门者具有极大的参考价值。

注意：本文讨论了最前沿的密码学技术，旨在提供一种利用「Julia Computing」进行研究的视角。请不要将文中的任何示例用于生产应用程序。在使用密码学之前一定要咨询专业的密码学专家。

程序包：https://github.com/JuliaComputing/ToyFHE.jl

相关代码：https://github.com/JuliaComputing/ToyFHE.jl/blob/master/examples/encrypted_mnist/infer.jl

引言

假设你开发了一个酷炫的新机器学习模型，现在你想将部署该模型，为用户提供服务。应该怎么做呢？最简单的方法可能是直接把模型发布给用户，然后让他们使用自己的数据在本地运行这个模型。但这种方法存在一些问题：

• 机器学习模型一般都很大，而用户的设备实际上可能没有足够的存储空间或算力来运行模型
• 机器学习模型一般都会频繁地更新，你可能不会想在网络上频繁传输这么大的模型
• 开发机器学习模型需要大量时间和计算资源，你可能会想通过向使用该模型的用户收费来收回成本

接下来，常用的解决方案是将模型作为应用程序接口（API）在云上公开。在过去几年间，这些「机器学习即服务」产品如雨后春笋般涌现，每个主要的云平台都会为企业级开发者提供这样的服务。

但这类产品的潜在用户所面对的困境也是显而易见的——处理用户数据的远程服务器可能并不可信。这样就会存在明确的伦理和法律的分歧，从而限制这种解决方案的有效范围。在受监管的产业（尤其是医疗业和金融业）中，一般是不允许将病患或金融数据发送给第三方进行处理的。我们可以做得更好吗？

事实证明，我们可以！最近，密码学方面取得的突破可以在无需进行解密的情况下，直接计算加密数据。在我们的例子中，用户可以将加密数据（例如图像）传递给云 API，以此运行机器学习模型，并返回加密的答案。整个过程中都没有解密用户数据，尤其是云服务商既不能访问原始图像，也不能解码计算得到的预测值。这是怎么做到的呢？本文通过构建一个进行加密图像的手写识别（来自 MNIST 数据集）的机器学习模型为大家揭秘背后的原理。

同态加密（Homomorphic Encryption，HE）的一般解释

一般而言，对加密数据进行计算的能力被称为「安全计算」，这是一个相当大的研究领域，针对大量不同的场景要用不同的密码学方法和技术解决问题。在本例中，我们将关注所谓的「同态加密」技术。在同态加密系统中，我们一般要进行以下操作：

pub_key, eval_key, priv_key = keygen() 
encrypted = encrypt(pub_key, plaintext) 
decrypted = decrypt(priv_key, encrypted) 
encrypted′ = eval(eval_key, f, encrypted) 

前三步非常直观，之前使用过任何非对称加密技术的人都会对此感到很熟悉（就像通过安全传输层协议（TLS）连接到本文）。最后一步才是神奇之处。它使用加密数据评估了 f，并返回了另一个与基于加密值评估 f 的结果对应的加密值。这一性质正是我们将这种技术称为「同态加密」的原因。评估操作与下面的加密操作等价：

f(decrypt(priv_key, encrypted)) == decrypt(priv_key, eval(eval_key, f, encrypted)) 

（同样地，可以基于加密值评估任意的同态 f）

支持哪些函数 f 取决于加密方案和支持的运算。如果只支持一种函数 f（比如 f=+），我们可以将这种加密方案称为「部分同态」。如果 f 是可以建立任意电路的完整的门的集合，如果电路大小有限，称之为「有限同态」（Somewhat Homomorphic Encryption, SHE）；如果电路大小不受限制，称之为「全同态」（Fully Homomorphic Encryption, FHE）。一般可以通过自助法（bootstrapping），将「有限」同态转换为「全」同态，但这个问题已经超过了本文所讨论的内容。

全同态加密是最近的研究，Craig Gentry 在 2009 年发表了第一个可行（但不实际）的方。现在陆续出现了一些更新也更实际的 FHE 方案。更重要的是，还有一些可以高效地实现这一方案的软件包。最常用的两个软件包是 Microsoft SEAL和 PALISADE。此外，我最近还开源了这些算法的 Julia 实现（https://github.com/JuliaComputing/ToyFHE.jl）。出于我们的目的，我们将使用后者中实现的 CKKS 加密。

高级 CKKS

CKKS（以 Cheon-Kim-Kim-Song 的名字命名，他在 2016 年的论文「Homomorphic Encryption for Arithmetic of Approximate Numbers」提出）是一种同态加密方案，可以对以下基本操作进行同态评估：

• 长度为 n 的复数向量的对应元素相加
• 长度为 n 的复数向量的对应元素相乘
• 向量中元素的旋转（通过循环移位实现）

向量元素的复共轭

这里的参数 n 取决于需要的安全性和准确性，该值一般都比较高。在本例中，n=4096（值越高越安全，但是计算开销也更大，时间复杂度大致会缩放为 nlog^n）。

此外，用 CKKS 计算是有噪声的。因此，计算结果一般都只是近似值，而且要注意确保评估结果足够准确，不会影响结果的正确性。

也就是说，对机器学习程序包的开发者而言，这些限制并不罕见。像 GPU 这样有特殊用途的加速器，也可以处理数字向量。同样，许多开发者会因算法选择的影响、多线程等原因，认为浮点数噪声太多（我要强调的是，有一个关键的区别是，浮点算法本身是确定性的，尽管因为实现的复杂性，它有时不会展现出这种确定性，但 CKKS 原语的噪声真的很多，但这也许可以让用户意识到噪声并没有第一次出现时那么可怕）。

考虑到这一点，我们再看看如何在 Julia 中执行这些运算（注意：这里有一些非常不安全的参数选择，这些操作的目的是说明这个库在交互式解释器（REPL）中的用法）。

julia> using ToyFHE  
  
# Let's play with 8 element vectors  
  
julia> N = 8;  
  
# Choose some parameters - we'll talk about it later  
  
julia> ℛ = NegacyclicRing(2N, (40, 40, *40*))  
ℤ₁₃₂₉₂₂₇₉₉₇₅₆₈₀₈₁₄₅₇₄₀₂₇₀₁₂₀₇₁₀₄₂₄₈₂₅₇/(x¹⁶ + 1)  
  
# We'll use CKKS julia> params = CKKSParams(ℛ)  
CKKS parameters  
  
# We need to pick a scaling factor for a numbers - again we'll talk about that later  
julia> Tscale = FixedRational{2^40}  
FixedRational{1099511627776,T} where T  
  
# Let's start with a plain Vector of zeros  
julia> plain = CKKSEncoding{Tscale}(zero(ℛ))  
8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7:  
0.0 + 0.0im  
0.0 + 0.0im  
0.0 + 0.0im  
0.0 + 0.0im  
0.0 + 0.0im  
0.0 + 0.0im  
0.0 + 0.0im  
0.0 + 0.0im  
  
# Ok, we're ready to get started, but first we'll need some keys  
julia> kp = keygen(params)  
CKKS key pair  
  
julia> kp.priv  
CKKS private key  
  
julia> kp.pub  
CKKS public key  
  
# Alright, let's encrypt some things:  
julia> foreach(i->plain[i] = i+1, 0:7); plain  
8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7:  
1.0 + 0.0im  
2.0 + 0.0im  
3.0 + 0.0im  
4.0 + 0.0im  
5.0 + 0.0im  
6.0 + 0.0im  
7.0 + 0.0im  
8.0 + 0.0im  
  
julia> c = encrypt(kp.pub, plain)  
CKKS ciphertext (length 2, encoding  
CKKSEncoding{FixedRational{1099511627776,T} where T}) 
 
# And decrypt it again 
julia> decrypt(kp.priv, c) 
8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7: 
0.9999999999995506 - 2.7335193113350057e-16im 
1.9999999999989408 - 3.885780586188048e-16im 
3.000000000000205 + 1.6772825551165524e-16im 
4.000000000000538 - 3.885780586188048e-16im 
4.999999999998865 + 8.382500573679615e-17im 
6.000000000000185 + 4.996003610813204e-16im 
7.000000000001043 - 2.0024593503998215e-16im 
8.000000000000673 + 4.996003610813204e-16im 
 
# Note that we had some noise. Let's go through all the primitive operations we'll need: 
 
julia> decrypt(kp.priv, c+c) 
8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7: 
1.9999999999991012 - 5.467038622670011e-16im 
3.9999999999978817 - 7.771561172376096e-16im 
6.00000000000041 + 3.354565110233105e-16im 
8.000000000001076 - 7.771561172376096e-16im 
9.99999999999773 + 1.676500114735923e-16im 
12.00000000000037 + 9.992007221626409e-16im 
14.000000000002085 - 4.004918700799643e-16im 
16.000000000001346 + 9.992007221626409e-16im 
 
julia> csq = c*c 
CKKS ciphertext (length 3, encoding CKKSEncoding{FixedRational{1208925819614629174706176,T} where T}) 
 
julia> decrypt(kp.priv, csq)8-element CKKSEncoding{FixedRational{1208925819614629174706176,T} where T} with indices 0:7: 
0.9999999999991012 - 2.350516767363621e-15im 
3.9999999999957616 - 5.773159728050814e-15im 
9.000000000001226 - 2.534464540987068e-15im 
16.000000000004306 - 2.220446049250313e-15im 
24.99999999998865 + 2.0903753311370056e-15im 
36.00000000000222 + 4.884981308350689e-15im 
49.000000000014595 + 1.0182491378134327e-15im 
64.00000000001077 + 4.884981308350689e-15im 

这很简单！敏锐的读者可能已经注意到了 csq 和之前的密文看起来有点不同。尤其是，它是「长度为 3」的密文，范围也更大。要说明它们是什么，以及它们是做什么用的有点太过复杂。我只想说，在进一步计算之前，我们要得让这些值降下来，否则我们会尽密文中的「空间」。幸运的是，有一种方法可以解决这两个问题：

# To get back down to length 2, we need to `keyswitch` (aka 
# relinerarize), which requires an evaluation key. Generating 
# this requires the private key. In a real application we would 
# have generated this up front and sent it along with the encrypted 
# data, but since we have the private key, we can just do it now. 
julia> ek = keygen(EvalMultKey, kp.priv) 
CKKS multiplication key 
 
julia> csq_length2 = keyswitch(ek, csq) 
CKKS ciphertext (length 2, encoding  
CKKSEncoding{FixedRational{1208925819614629174706176,T} where T}) 
 
 
# Getting the scale back down is done using modswitching. 
julia> csq_smaller = modswitch(csq_length2) 
 
CKKS ciphertext (length 2, encoding  
CKKSEncoding{FixedRational{1.099511626783e12,T} where T}) 
 
 
# And it still decrypts correctly (though note we've lost some precision) 
julia> decrypt(kp.priv, csq_smaller) 
8-element CKKSEncoding{FixedRational{1.099511626783e12,T} where T} with indices 0:7: 
0.9999999999802469 - 5.005163520332181e-11im 
3.9999999999957723 - 1.0468514951188039e-11im 
8.999999999998249 - 4.7588542623100616e-12im 
16.000000000023014 - 1.0413447889166631e-11im 
24.999999999955193 - 6.187833723406491e-12im 
36.000000000002345 + 1.860733715346631e-13im 
49.00000000001647 - 1.442396043149794e-12im 
63.999999999988695 - 1.0722489563648028e-10im 

 

 

 

此外，modswitching（模转换：modulus switching 的简写）减少了密文模的大小，所以我们不能无限地这么做下去。（用上文提到的术语来说，我们在这里使用的是 SHE 方案）：

 

julia> ℛ # Remember the ring we initially created 
ℤ₁₃₂₉₂₂₇₉₉₇₅₆₈₀₈₁₄₅₇₄₀₂₇₀₁₂₀₇₁₀₄₂₄₈₂₅₇/(x¹⁶ + 1) 
 
julia> ToyFHE.ring(csq_smaller) # It shrunk! 
ℤ₁₂₀₈₉₂₅₈₂₀₁₄₄₅₉₃₇₇₉₃₃₁₅₅₃/(x¹⁶ + 1) 

我们要做的最后一步运算是：旋转。就像上文的密钥转换（KeySwitching），在这里也需要评估密钥（也称为伽罗瓦（galois）密钥）：

julia> gk = keygen(GaloisKey, kp.priv; steps=2) 
CKKS galois key (element 25) 
 
julia> decrypt(circshift(c, gk)) 
decrypt(kp, circshift(c, gk)) 
8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7: 
7.000000000001042 + 5.68459112632516e-16im 
8.000000000000673 + 5.551115123125783e-17im 
0.999999999999551 - 2.308655353580721e-16im 
1.9999999999989408 + 2.7755575615628914e-16im 
3.000000000000205 - 6.009767921608429e-16im 
4.000000000000538 + 5.551115123125783e-17im 
4.999999999998865 + 4.133860996136768e-17im 
6.000000000000185 - 1.6653345369377348e-16im 
 
# And let's compare to doing the same on the plaintext 
julia> circshift(plain, 2) 
8-element OffsetArray(::Array{Complex{Float64},1}, 0:7) with eltype Complex{Float64} with indices 0:7: 
7.0 + 0.0im 
8.0 + 0.0im 
1.0 + 0.0im 
2.0 + 0.0im 
3.0 + 0.0im 
4.0 + 0.0im 
5.0 + 0.0im 
6.0 + 0.0im 

好了，我们已经了解了同态加密库的基本用法。在思考如何用这些原语进行神经网络推断之前，我们先观察并训练我们需要使用的神经网络。

机器学习模型

如果你不熟悉机器学习或 Flux.jl 机器学习库，我建议你先快速阅读一下 Flux.jl 文档或我们在 JuliaAcademy 上发布的免费机器学习介绍课程，因为我们只会讨论在加密数据上运行模型所做的更改。

我们将以 Flux 模型空间中卷积神经网络的例子为出发点。在这个模型中，训练循环、数据预处理等操作都不变，只是轻微地调整模型。我们要用的模型是：

function reshape_and_vcat(x) 
let y=reshape(x, 64, 4, size(x, 4)) 
vcat((y[:,i,:] for i=axes(y,2))...) 
end 
end 
 
model = Chain( 
# First convolution, operating upon a 28x28 image 
Conv((7, 7), 1=>4, stride=(3,3), x->x.^2), 
reshape_and_vcat, 
Dense(256, 64, x->x.^2), 
Dense(64, 10), 
) 

该模型与「安全外包矩阵的计算及其在神经网络上与应用」（Secure Outsourced Matrix Computation and Application to Neural Networks）文中所用的模型基本相同，它们用相同的加密方案演示了相同的模型，但有两个区别：（1）他们加密了模型而我们（为简单起见）没有对模型加密；（2）我们在每一层之后都有偏置向量（这也是 Flux 的默认行为），我不确定这种行为对本文评估的模型是否是这样。也许是因为（2），我们模型的准确率才略高（98.6% vs 98.1%），但这也可能仅仅是因为超参数的差异。

「x.^2」激活函数也是一个不寻常的特征（对那些有机器学习背景的人来说）。这里更常用的选择可能是「tanh」、「relu」或者其他更高级的函数。然而，尽管这些函数（尤其是 relu）可以更容易地评估明文值，但评估加密数据的计算开销则相当大（基本上是评估多项式近似值）。幸运的是，「x.^2」可以很好地满足我们的目的。

其余的训练循环基本上是相同的。我们从模型中删除了「softmax」，取而代之的是「logitcrossentropy」损失函数（当然也可以保留它，在客户端解密后再评估「softmax」）。训练模型的完整代码见 GitHub，在近期发布的 GPU 上只需要几分钟就可以完成训练。

代码地址：https://github.com/JuliaComputing/ToyFHE.jl/blob/master/examples/encrypted_mnist/train.jl

高效地计算

好了，现在已经明确了我们需要做什么，接下来看看我们要做哪些运算：

• 卷积
•  元素平方
•  矩阵乘法

我们在上文中已经看到了，元素平方操作是很简单的，所以我们按顺序处理剩下的两个问题。在整个过程中，假设批处理大小（batch size）为 64（你可能注意到了，我们有策略地选择模型参数和批处理大小，从而充分利用 4096 元素向量的优势，这是我们从实际的参数选择中得到的）。

卷积

让我们回顾一下卷积是如何工作的。首先，取原始输入数组中的一些窗口（本例中为 7*7），窗口中的每个元素跟卷积掩模的元素相乘。然后移动窗口（本例中步长为 3，所以将窗口移动 3 个元素）。重复这个过程（用相同的卷积掩模）。下面的动画说明了以（2，2）的步长进行 3*3 卷积的过程（蓝色数组是输入，绿色数组是输出）。

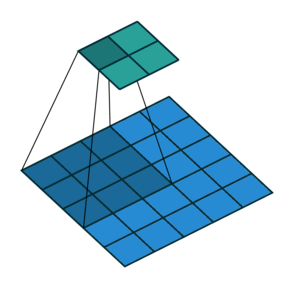
另外，我们将卷积分成 4 个不同的「通道」（这意味着用不同的卷积掩模，将卷积又重复了 3 次）

好了，现在我们已经知道了要做什么，接下来考虑一下该如何实现。幸运的是，卷积是我们模型中的第一步运算。因此，可以在加密数据之前（无需模型权重）先在客户端上预处理，来节省一些工作。具体而言，我们将执行以下操作：

•  预先计算每个卷积窗口（即从原始图像中提取 7*7 的窗口），从每个输入图像中得到 64 个 7*7 的矩阵（注意要在步长为 2 的情况下得到 7*7 的窗口，要评估 28*28 的输入图像的话，要计算 8*8 的卷积窗口）
•  将每个窗口中的相同位置收集到一个向量中，即对每张图来说，都会有包含 64 个元素的向量，或当批处理大小为 64 时，会得到 64*64 的元素向量（即，共有 49 个 64*64 的矩阵）
•  加密

然后卷积就变成了整个矩阵和适当掩码元素的标量乘法，对这 49 个元素求和，得到了卷积的结果。这个方案是这样实现的（在明文上）：

function public_preprocess(batch) 
ka = OffsetArray(0:7, 0:7) 
# Create feature extracted matrix 
I = [[batch[i′*3 .+ (1:7), j′*3 .+ (1:7), 1, k] for i′=ka, j′=ka] for k = 1:64] 
 
# Reshape into the ciphertext 
Iᵢⱼ = [[I[k][l...][i,j] for k=1:64, l=product(ka, ka)] for i=1:7, j=1:7] 
end 
 
Iᵢⱼ = public_preprocess(batch) 
 
# Evaluate the convolution 
weights = model.layers[1].weight 
conv_weights = reverse(reverse(weights, dims=1), dims=2) 
conved = [sum(Iᵢⱼ[i,j]*conv_weights[i,j,1,channel] for i=1:7, j=1:7) for channel = 1:4] 
conved = map(((x,b),)->x .+ b, zip(conved, model.layers[1].bias)) 

这样的实现（对维度重新排序的模）给出了相同的答案，但是用了这样的操作：

model*.*layers[*1*](batch) 

加入加密操作后，我们得到：

Iᵢⱼ = public_preprocess(batch)  
C_Iᵢⱼ = map(Iᵢⱼ) do Iij  
plain = CKKSEncoding{Tscale}(zero(plaintext_space(ckks_params)))  
plain .= OffsetArray(vec(Iij), 0:(N÷2-1))  
encrypt(kp, plain)  
end  
  
weights = model.layers[1].weight  
conv_weights = reverse(reverse(weights, dims=1), dims=2)  
conved3 = [sum(C_Iᵢⱼ[i,j]*conv_weights[i,j,1,channel] for i=1:7, j=1:7) for channel = 1:4]  
conved2 = map(((x,b),)->x .+ b, zip(conved3, model.layers[1].bias))  
conved1 = map(ToyFHE.modswitch, conved2)  

注意，由于权重是公开的，所以不需要密钥转换，因此没有扩展密文的长度。

矩阵乘法

接下来看看矩阵乘法是如何实现的。我们利用这样的事实——可以旋转向量中的元素，来重排序乘法索引。特别是，要考虑向量中矩阵元素的行优先排序。然后，如果以行大小的倍数移动向量，就可以得到列旋转的效果，这可以提供充足的原语来实现矩阵乘法（至少是方阵）。我们不妨试一下：

function matmul_square_reordered(weights, x) 
sum(1:size(weights, 1)) do k 
# We rotate the columns of the LHS and take the diagonal 
weight_diag = diag(circshift(weights, (0,(k-1)))) 
# We rotate the rows of the RHS 
x_rotated = circshift(x, (k-1,0)) 
# We do an elementwise, broadcast multiply 
weight_diag .* x_rotated 
end 
end 
 
function matmul_reorderd(weights, x) 
sum(partition(1:256, 64)) do range 
matmul_square_reordered(weights[:, range], x[range, :]) 
end 
end 
 
fc1_weights = model.layers[3].W 
x = rand(Float64, 256, 64) 
@assert (fc1_weights*x) ≈ matmul_reorderd(fc1_weights, x) 

当然，对于一般的矩阵乘法，我们可能需要更好的方法，但是在本例中，现在这种程度就已经足够了。

优化代码

至此，我们设法将所有内容整合在一起，而且也确实奏效了。这里提供了代码作为参考（省略了参数选择等设置）：

ek = keygen(EvalMultKey, kp.priv) 
gk = keygen(GaloisKey, kp.priv; steps=64) 
 
Iᵢⱼ = public_preprocess(batch) 
C_Iᵢⱼ = map(Iᵢⱼ) do Iij 
plain = CKKSEncoding{Tscale}(zero(plaintext_space(ckks_params))) 
plain .= OffsetArray(vec(Iij), 0:(N÷2-1)) 
encrypt(kp, plain) 
end 
 
weights = model.layers[1].weight 
conv_weights = reverse(reverse(weights, dims=1), dims=2) 
conved3 = [sum(C_Iᵢⱼ[i,j]*conv_weights[i,j,1,channel] for i=1:7, j=1:7) for channel = 1:4] 
conved2 = map(((x,b),)->x .+ b, zip(conved3, model.layers[1].bias)) 
conved1 = map(ToyFHE.modswitch, conved2) 
 
Csqed1 = map(x->x*x, conved1) 
Csqed1 = map(x->keyswitch(ek, x), Csqed1) 
Csqed1 = map(ToyFHE.modswitch, Csqed1) 
 
function encrypted_matmul(gk, weights, x::ToyFHE.CipherText) 
result = repeat(diag(weights), inner=64).*x 
rotated = x 
for k = 2:64 
rotated = ToyFHE.rotate(gk, rotated) 
result += repeat(diag(circshift(weights, (0,(k-1)))), inner=64) .* rotated 
end 
result 
end 
 
fq1_weights = model.layers[3].W 
Cfq1 = sum(enumerate(partition(1:256, 64))) do (i,range) 
encrypted_matmul(gk, fq1_weights[:, range], Csqed1[i]) 
end 
 
Cfq1 = Cfq1 .+ OffsetArray(repeat(model.layers[3].b, inner=64), 0:4095) 
Cfq1 = modswitch(Cfq1) 
 
Csqed2 = Cfq1*Cfq1 
Csqed2 = keyswitch(ek, Csqed2) 
Csqed2 = modswitch(Csqed2) 
 
function naive_rectangular_matmul(gk, weights, x) 
@assert size(weights, 1) < size(weights, 2) 
weights = vcat(weights, zeros(eltype(weights), size(weights, 2)-size(weights, 1), size(weights, 2))) 
encrypted_matmul(gk, weights, x) 
end 
 
fq2_weights = model.layers[4].W 
Cresult = naive_rectangular_matmul(gk, fq2_weights, Csqed2)Cresult = Cresult .+ OffsetArray(repeat(vcat(model.layers[4].b,  
zeros(54)), inner=64), 0:4095) 

虽然代码看起来不是很清晰，但是如果你已经进行到这一步了，那你就应该理解这个流程中的每一步。

现在，把注意力转移到可以让这一切更好理解的抽象上。我们先跳出密码学和机器学习领域，考虑编程语言设计的问题。Julia 可以实现强大的抽象，我们可以利用这一点构建一些抽象。例如，可以将整个卷积提取过程封装为自定义数组类型：

using BlockArrays 
 
""" 
    ExplodedConvArray{T, Dims, Storage} <: AbstractArray{T, 4} 
 
Represents a an `nxmx1xb` array of images, but rearranged into a 
series of convolution windows. Evaluating a convolution compatible 
with `Dims` on this array is achievable through a sequence of 
scalar multiplications and sums on the underling storage. 
""" 
struct ExplodedConvArray{T, Dims, Storage} <: AbstractArray{T, 4} 
    # sx*sy matrix of b*(dx*dy) matrices of extracted elements 
    # where (sx, sy) = kernel_size(Dims) 
    #       (dx, dy)=output_size(DenseConvDims(...)) 
    cdims::Dims 
    x::Matrix{Storage} 
    function ExplodedConvArray{T, Dims, Storage}(cdims::Dims, storage::Matrix{Storage}) where {T, Dims, Storage} 
        @assert all(==(size(storage[1])), size.(storage)) 
        new{T, Dims, Storage}(cdims, storage) 
    end 
end 
Base.size(ex::ExplodedConvArray) = (NNlib.input_size(ex.cdims)..., 1, size(ex.x[1], 1)) 
 
function ExplodedConvArray{T}(cdims, batch::AbstractArray{T, 4}) where {T} 
    x, y = NNlib.output_size(cdims) 
    kx, ky = NNlib.kernel_size(cdims) 
    stridex, stridey = NNlib.stride(cdims) 
    kax = OffsetArray(0:x-1, 0:x-1) 
    kay = OffsetArray(0:x-1, 0:x-1) 
    I = [[batch[i′*stridex .+ (1:kx), j′*stridey .+ (1:ky), 1, k] for i′=kax, j′=kay] for k = 1:size(batch, 4)] 
Iᵢⱼ = [[I[k][l...][i,j]  
for k=1:size(batch, 4), l=product(kax, kay)] for (i,j) in product(1:kx, 1:ky)] 
 
ExplodedConvArray{T, typeof(cdims), eltype(Iᵢⱼ)}(cdims, Iᵢⱼ) 
end 
 
function NNlib.conv(x::ExplodedConvArray{<:Any, Dims},  
weights::AbstractArray{<:Any, 4}, cdims::Dims) where {Dims<:ConvDims} 
blocks = reshape([  
Base.ReshapedArray(sum(x.x[i,j]*weights[i,j,1,channel] for i=1:7, j=1:7), (NNlib.output_size(cdims)...,1,size(x, 4)), ()) for channel = 1:4 ],(1,1,4,1)) 
BlockArrays._BlockArray(blocks, BlockArrays.BlockSizes([8], [8], [1,1,1,1], [64])) 
end 

注意，如原始代码所示，这里用 BlockArrays 将 8*8*4*64 的数组表示成 4 个 8*8*1*64 的数组。所以现在，我们已经得到了第一个步骤更好的表征（至少是在未加密数组上）：

julia> cdims = DenseConvDims(batch, model.layers[1].weight; stride=(3,3), padding=(0,0,0,0), dilation=(1,1)) 
DenseConvDims: (28, 28, 1) * (7, 7) -> (8, 8, 4), stride: (3, 3) pad: (0, 0, 0, 0), dil: (1, 1), flip: false 
 
julia> a = ExplodedConvArray{eltype(batch)}(cdims, batch); 
julia> model(a) 
10×64 Array{Float32,2}: 
[snip]如何将这种表征带入加 

如何将这种表征带入加密的世界呢？我们需要做两件事：

1. 我们想以这样的方式加密结构体（ExplodedConvArray），以致于对每个字段（field）都能得到一个密文。然后，通过查询该函数在原始结构上执行的操作，在加密的结构体上进行运算，并直接进行相同的同态操作。

2. 我们希望拦截某些在加密的上下文中以不同方式执行的操作。

 

幸运的是 Julia 提供了可以同时执行这两个操作的抽象：使用 Cassette.jl 机制的编译器插件。它是如何起作用的，以及如何使用它，都有些复杂，本文中不再深入介绍这部分内容。简言之，你可以定义上下文（即「Excrypted」，然后定义在这样的上下文中，运算是如何起作用的规则）。例如，第二个要求可以写成：

所有这一切的最终结果是，用户可以以最少的手工工作，写完整个内容：

当然，就算经过了以上处理，代码也不是最优的。加密系统的参数（例如 ℛ 环，什么时候模转换，什么时候密钥转换等）表现出了在答案的准确性、安全性以及性能之间的取舍，而且参数很大程度上取决于正在运行的代码。一般来说，人们希望编译器能分析将要运行的加密代码，为给定的安全等级和所需精度提出参数建议，然后用户以最少的人工操作来生成代码。

结语

对于任何系统来说，安全地自动执行任意计算都是一项艰巨的任务，但 Julia 的元编程功能和友好的语法都让它成为合适的开发平台。RAMPARTS 系统已经做了一些尝试，将简单的 Julia 代码编译到 PALISADE FHE 库中。「Julia Computing」正在与 RAMPARTS 背后的专家在 Verona 平台上合作，最近已经发布了下一代版本。在过去的一年中，同态加密系统的性能才达到能以实际可用的速度评估有趣计算的程度。一扇崭新的大门就此打开。随着算法、软件和硬件的进步，同态加密必然会成为保护数百万用户隐私的主流技术。

RAMPARTS 论文：https://eprint.iacr.org/2019/988.pdf

报告：https://www.youtube.com/watch?v=_KLlMg6jKQg