导读
因为图分析是数据科学家的未来。
作为数据科学家,我们对pandas、SQL或任何其他关系数据库非常熟悉。
我们习惯于将用户的属性以列的形式显示在行中。但现实世界真的是这样吗?
在一个互联的世界里,用户不能被视为独立的实体。它们之间有一定的关系,我们在建立机器学习模型的时候,有时也会考虑这些关系。
现在,虽然在关系数据库中,我们不能在不同的行(用户)之间使用这样的关系,但是在图形数据库中,这样做非常简单。
在本文中,我将讨论一些你应该知道的最重要的图算法,以及如何使用Python实现它们。
1. 连通组件
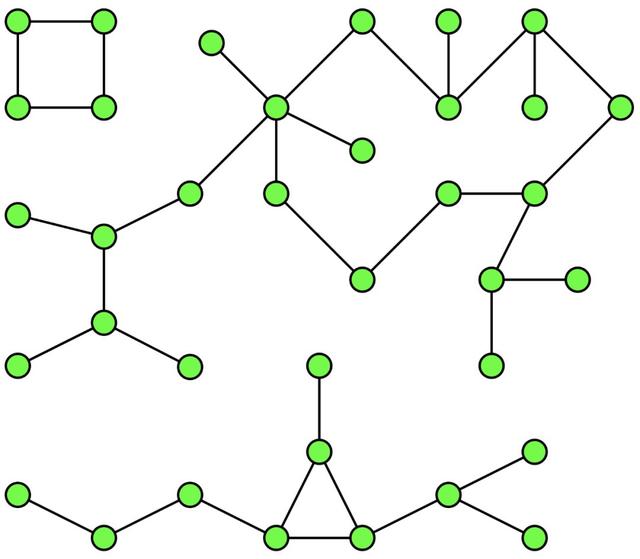
一个包含3个连通组件的图
我们都知道聚类是如何工作的。
你可以用外行人的术语来理解连通组件,它是一种硬聚类算法,可以在相关/连接的数据中找到聚类/岛屿
举个具体的例子:假设你有连接世界上任何两个城市的道路的数据。你需要找出世界上所有的大陆以及它们包含哪些城市
你将如何实现这一点?来想想吧。
我们使用的连通组件算法是基于BFS/DFS的特殊情况。我不会在这里过多地讨论它是如何工作的,但是我们将看到如何使用Networkx编写和运行代码。
应用
从零售的角度来看:假设我们有很多客户,使用很多账户。使用连通组件算法的一种方法是在数据集中找出明显不同的家族。
我们可以根据相同的信用卡使用情况、相同的地址或相同的移动电话号码等设定客户ID之间的边(路)。一旦我们有了这些连接,我们就可以运行连通组件算法来创建单独的簇,然后我们可以为其分配一个家族ID。
然后,我们可以使用这些家族ID根据家族需求提供个性化的推荐。我们还可以使用这个家族ID,通过创建基于家族的分组特征来支持我们的分类算法。
从财务的角度来看:另一个用例是使用这些家族ID捕获欺诈。如果一个账户在过去有过欺诈行为,关联账户很可能也容易进行欺诈。
可能性只受你自己想象力的限制。
代码
我们将使用Python中的Networkx模块来创建和分析图。
让我们从一个示例图开始,我们使用它来实现我们的目的。包含城市和城市之间的距离信息。
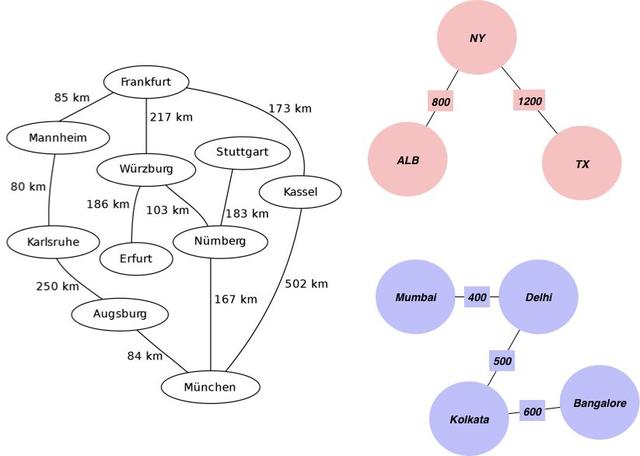
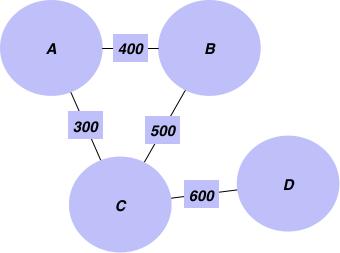
使用随机距离的图
我们首先创建一个带有距离的边的列表,我们把距离作为边的权重:
- edgelist = [['Mannheim', 'Frankfurt', 85], ['Mannheim', 'Karlsruhe', 80], ['Erfurt', 'Wurzburg', 186], ['Munchen', 'Numberg', 167], ['Munchen', 'Augsburg', 84], ['Munchen', 'Kassel', 502], ['Numberg', 'Stuttgart', 183], ['Numberg', 'Wurzburg', 103], ['Numberg', 'Munchen', 167], ['Stuttgart', 'Numberg', 183], ['Augsburg', 'Munchen', 84], ['Augsburg', 'Karlsruhe', 250], ['Kassel', 'Munchen', 502], ['Kassel', 'Frankfurt', 173], ['Frankfurt', 'Mannheim', 85], ['Frankfurt', 'Wurzburg', 217], ['Frankfurt', 'Kassel', 173], ['Wurzburg', 'Numberg', 103], ['Wurzburg', 'Erfurt', 186], ['Wurzburg', 'Frankfurt', 217], ['Karlsruhe', 'Mannheim', 80], ['Karlsruhe', 'Augsburg', 250],["Mumbai", "Delhi",400],["Delhi", "Kolkata",500],["Kolkata", "Bangalore",600],["TX", "NY",1200],["ALB", "NY",800]]
使用Networkx构建图:
- g = nx.Graph()
- for edge in edgelist:
- g.add_edge(edge[0],edge[1], weight = edge[2])
现在我们想从这张图中找出不同的大陆及其包含的城市。
我们现在可以使用连通组件算法做到这一点:
- for i, x in enumerate(nx.connected_components(g)):
- print("cc"+str(i)+":",x)
- ------------------------------------------------------------
- cc0: {'Frankfurt', 'Kassel', 'Munchen', 'Numberg', 'Erfurt', 'Stuttgart', 'Karlsruhe', 'Wurzburg', 'Mannheim', 'Augsburg'}
- cc1: {'Kolkata', 'Bangalore', 'Mumbai', 'Delhi'}
- cc2: {'ALB', 'NY', 'TX'}
正如你所看到的,我们能够在数据中找到不同的部分。只需要使用边和顶点。这个算法可以在不同的数据上运行,以满足我上面提到的任何用例。
2. 最短路径
继续上面的例子,我们得到了一个德国城市的图以及它们之间的距离。
你想知道如何从法兰克福(起始节点)到慕尼黑的最短距离。
我们用来解决这个问题的算法叫做Dijkstra。用Dijkstra自己的话来说:
- 从鹿特丹到[格罗宁根的最短路线是什么?一般来说,最短路径的算法是这样的,我花了大约20分钟来设计它。一天早上我在阿姆斯特丹和我的年轻的未婚妻购物,累了,我们坐在咖啡馆露台喝一杯咖啡,我就在想我能不能想出这个最短路径算法,然后我就想出来了。正如我所说,这是一个20分钟的发明。事实上,它是在1959年出版的。三年后,还可以读到,事实上,它相当不错。它如此漂亮的原因之一是我不用铅笔和纸来设计它。后来我了解到,不用铅笔和纸设计的好处之一是,你几乎不得不避免所有可以避免的复杂性。最终,令我大为惊讶的是,这个算法成了我成名的基石之一。
- Edsger Dijkstra,在对Philip L. Frana的采访中
应用
Dijkstra算法的变体广泛应用于谷歌地图中,用于寻找最短路径。
你在沃尔玛,你有不同的通道和所有通道之间的距离。你想要提供从A通道到D通道到客户的最短路径。
你可以看到LinkedIn如何显示1级和2级的连接。幕后发生了什么?
代码
- print(nx.shortest_path(g, 'Stuttgart','Frankfurt',weight='weight'))
- print(nx.shortest_path_length(g, 'Stuttgart','Frankfurt',weight='weight'))
- --------------------------------------------------------
- ['Stuttgart', 'Numberg', 'Wurzburg', 'Frankfurt']
- 503
你也可以找到所有的地点对之间的最短路径:
- for x in nx.all_pairs_dijkstra_path(g,weight='weight'):
- print(x)
- --------------------------------------------------------
- ('Mannheim', {'Mannheim': ['Mannheim'], 'Frankfurt': ['Mannheim', 'Frankfurt'], 'Karlsruhe': ['Mannheim', 'Karlsruhe'], 'Augsburg': ['Mannheim', 'Karlsruhe', 'Augsburg'], 'Kassel': ['Mannheim', 'Frankfurt', 'Kassel'], 'Wurzburg': ['Mannheim', 'Frankfurt', 'Wurzburg'], 'Munchen': ['Mannheim', 'Karlsruhe', 'Augsburg', 'Munchen'], 'Erfurt': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Erfurt'], 'Numberg': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg'], 'Stuttgart': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']})
- ('Frankfurt', {'Frankfurt': ['Frankfurt'], 'Mannheim': ['Frankfurt', 'Mannheim'], 'Kassel': ['Frankfurt', 'Kassel'], 'Wurzburg': ['Frankfurt', 'Wurzburg'], 'Karlsruhe': ['Frankfurt', 'Mannheim', 'Karlsruhe'], 'Augsburg': ['Frankfurt', 'Mannheim', 'Karlsruhe', 'Augsburg'], 'Munchen': ['Frankfurt', 'Wurzburg', 'Numberg', 'Munchen'], 'Erfurt': ['Frankfurt', 'Wurzburg', 'Erfurt'], 'Numberg': ['Frankfurt', 'Wurzburg', 'Numberg'], 'Stuttgart': ['Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']})
- ....
3. 最小生成树
现在我们有另一个问题。我们为一家水管铺设公司或互联网光纤公司工作。我们需要用最少的电线/管道连接图中所有的城市,我们该怎么做?
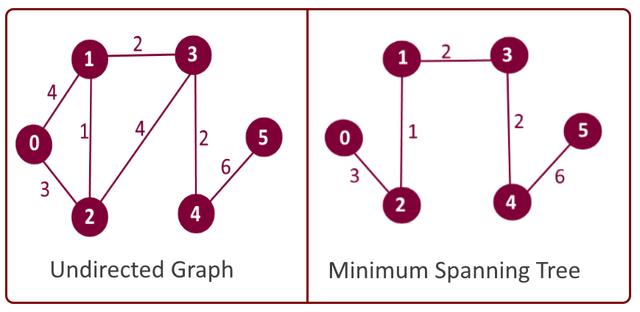
一个无向图,右边是它的最小生成树
应用
- 最小生成树直接应用于网络设计,包括计算机网络、电信网络、交通网络、供水网络和电网(它们最初是为这些网络而发明的)
- MST用于逼近旅行商问题
- 聚类 — 首先构造MST,然后使用簇间距离和簇内距离确定MST中某些边缘的分割阈值。
- 图像分割 — 用于图像分割,我们首先在一个图上构造一个MST,其中像素是节点,像素之间的距离基于一些相似性度量(颜色、强度等)。
代码
- # nx.minimum_spanning_tree(g) returns a instance of type graph
- nx.draw_networkx(nx.minimum_spanning_tree(g))
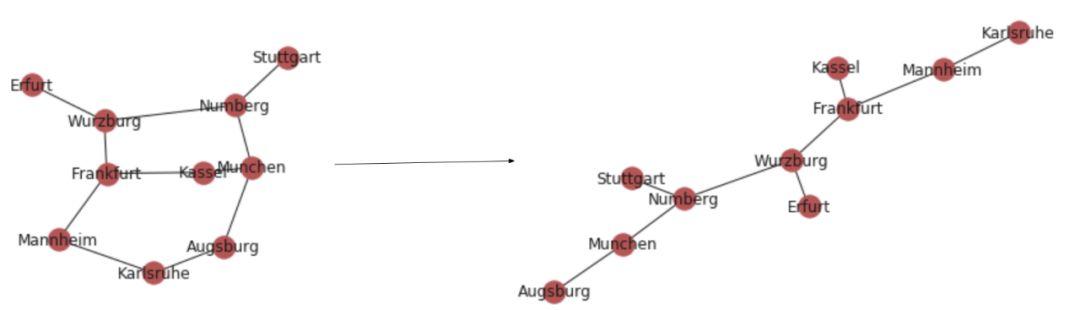
我们的图的最小生成树
可以看到,上面就是我们需要铺设的电线。
4. Pagerank
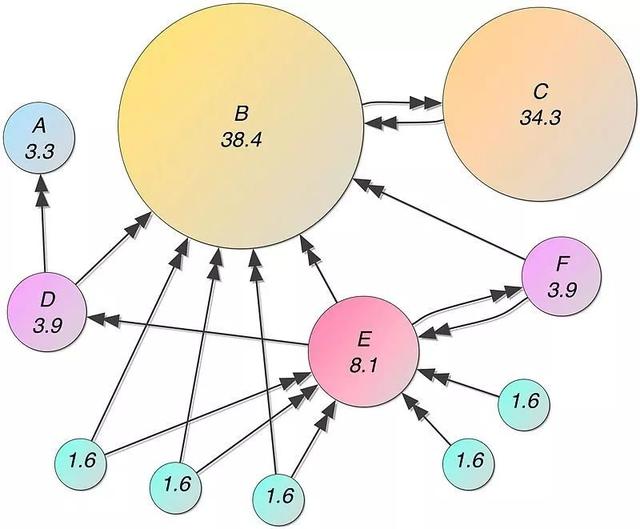
这就是长期以来支持谷歌的页面排序算法。它根据输入和输出链接的数量和质量为页面分配一个分数。
应用
Pagerank可以用于任何我们想要估计任何网络中节点重要性的地方。
- 它被用来寻找最具影响力的论文使用引文。
- 被谷歌用来排列页面
- 它可以用来把tweets-用户和以及tweets-tweets当成节点进行排序。如果用户A关注了用户B,那么创建用户之间的链接,如果用户tweet/retwets一条tweet,则创建用户和tweet之间的链接。
- 推荐引擎
代码
在这个练习中,我们将使用Facebook数据。我们有一个facebook用户之间的边/链接文件。我们首先创建FB图,使用:
- # reading the dataset
- fb = nx.read_edgelist('../input/facebook-combined.txt', create_using = nx.Graph(), nodetype = int)
它是这样的:
- pos = nx.spring_layout(fb)
- import warnings
- warnings.filterwarnings('ignore')
- plt.style.use('fivethirtyeight')
- plt.rcParams['figure.figsize'] = (20, 15)
- plt.axis('off')
- nx.draw_networkx(fb, pos, with_labels = False, node_size = 35)
- plt.show()
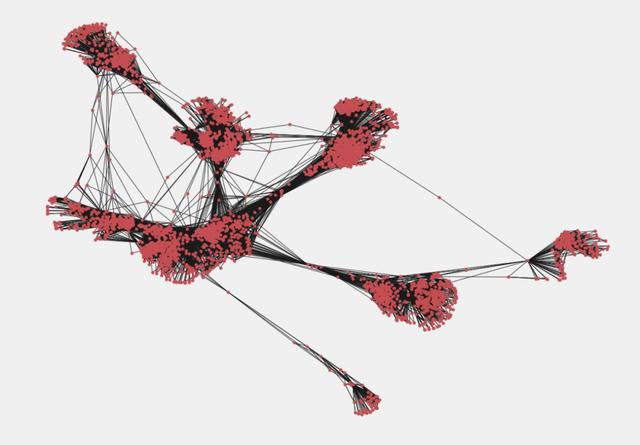
FaceBook用户图
现在我们想要找到具有高影响力的用户。
直观地说,Pagerank算法会给有很多朋友的用户打高分,而这些朋友又有很多facebook上的朋友。
- pageranks = nx.pagerank(fb)
- print(pageranks)
- ------------------------------------------------------
- {0: 0.006289602618466542,
- 1: 0.00023590202311540972,
- 2: 0.00020310565091694562,
- 3: 0.00022552359869430617,
- 4: 0.00023849264701222462,
- ........}
我们可以用PageRank得到最有影响力的用户排序:
- import operator
- sorted_pagerank = sorted(pageranks.items(), key=operator.itemgetter(1),reverse = True)
- print(sorted_pagerank)
- ------------------------------------------------------
- [(3437, 0.007614586844749603), (107, 0.006936420955866114), (1684, 0.0063671621383068295), (0, 0.006289602618466542), (1912, 0.0038769716008844974), (348, 0.0023480969727805783), (686, 0.0022193592598000193), (3980, 0.002170323579009993), (414, 0.0018002990470702262), (698, 0.0013171153138368807), (483, 0.0012974283300616082), (3830, 0.0011844348977671688), (376, 0.0009014073664792464), (2047, 0.000841029154597401), (56, 0.0008039024292749443), (25, 0.000800412660519768), (828, 0.0007886905420662135), (322, 0.0007867992190291396),......]
以上id适用于最有影响力的用户。
我们可以看到最具影响力用户的子图:
- first_degree_connected_nodes = list(fb.neighbors(3437))
- second_degree_connected_nodes = []
- for x in first_degree_connected_nodes:
- second_degree_connected_nodes+=list(fb.neighbors(x))
- second_degree_connected_nodes.remove(3437)
- second_degree_connected_nodes = list(set(second_degree_connected_nodes))
- subgraph_3437 = nx.subgraph(fb,first_degree_connected_nodes+second_degree_connected_nodes)
- pos = nx.spring_layout(subgraph_3437)
- node_color = ['yellow' if v == 3437 else 'red' for v in subgraph_3437]
- node_size = [1000 if v == 3437 else 35 for v in subgraph_3437]
- plt.style.use('fivethirtyeight')
- plt.rcParams['figure.figsize'] = (20, 15)
- plt.axis('off')
- nx.draw_networkx(subgraph_3437, pos, with_labels = False, node_color=node_color,node_size=node_size )
- plt.show()
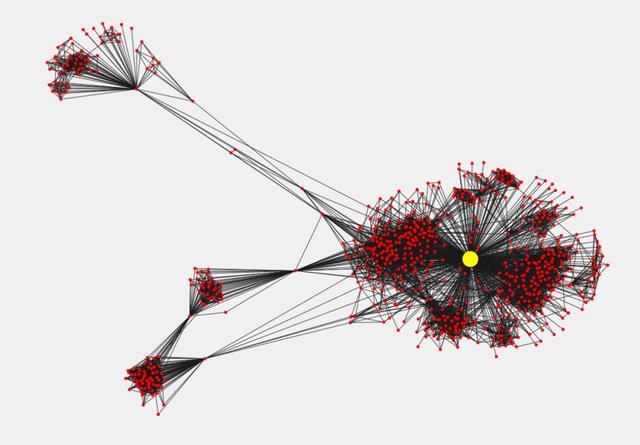
最有影响力的用户(黄色)
5. 中心度量
有许多中心度量,你都可以将其用作机器学习模型的特征。我将讨论其中的两个。
- 内中心:重要的不仅是拥有最多朋友的用户,将一个地理位置与另一个地理位置连接起来的用户也很重要,因为这让用户可以看到来自不同地理位置的内容。内中心度量了一个特定节点在另外两个节点之间的最短路径中出现的次数
- 度中心:它是节点的连接数。
应用
中心度量可以作为任何机器学习模型的一个特征。
代码
面的代码用于查找子图的内中心。
- pos = nx.spring_layout(subgraph_3437)
- betweennessCentrality = nx.betweenness_centrality(subgraph_3437,normalized=True, endpoints=True)
- node_size = [v * 10000 for v in betweennessCentrality.values()]
- plt.figure(figsize=(20,20))
- nx.draw_networkx(subgraph_3437, pos=pos, with_labels=False, node_size=node_size )
- plt.axis('off')
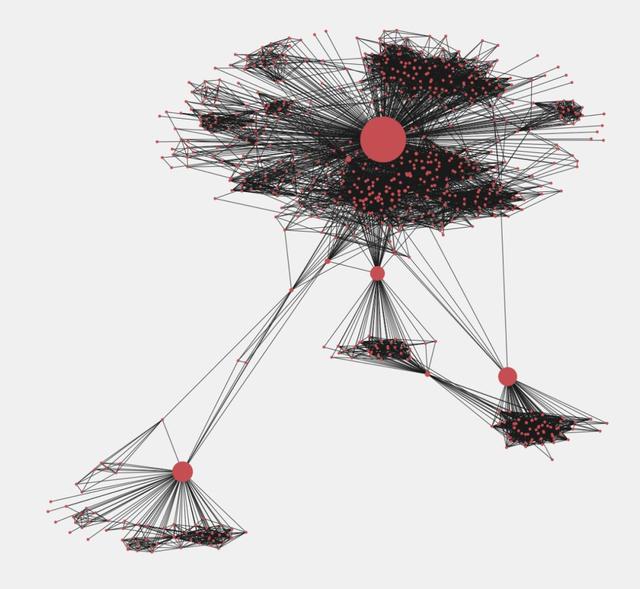
可以看到,在这里按它们的内中心值调整节点的大小。他们可以被认为是信息传递者。将具有高内中心的任何节点断开将会将图分成许多部分。
总结
在这篇文章中,我讨论了一些最具影响力的图算法,它们改变了我们的生活方式
随着如此多的社会数据的出现,网络分析可以在很大程度上帮助我们改进模型和产生价值。
甚至更多地了解这个世界。