概述
对OSPF有所了解的小伙伴都应该知道,在mult-access(多点接入)的网络中,是需要选择DR/BDR的,不然会出现N平方的问题,增加网络开销。那什么是N平方问题呢?我们来看一下。
邻接关系中的N平方问题
如下图所示,在同一个网段上,如果这4个路由器之间要想交换所有的路由(LSA)信息,必须要两两形成邻接关系:
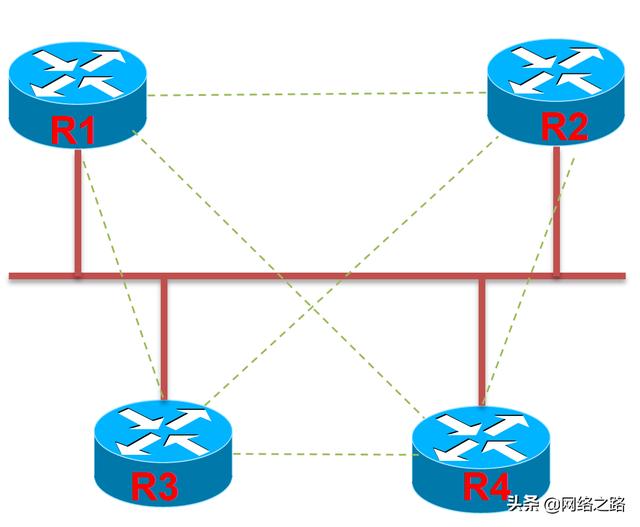
N平方问题
这里有一个计算公式:邻接的数量 = n(n-1)/2,n表示路由器数量;
路由器越多,则需要形成的邻接关系就越多,并且成倍的增长,这就是我们所说的N平方问题。
例如4个路由器,总共要形成6个邻接关系;5个路由器,会形成10个邻接关系;6个路由器,会形成15个邻接关系;
而每一个邻接关系之间都需要交换路由(LSA)信息,这样不仅会占用网络的带宽,每台路由器也会收到同一条路由的多条拷贝(copy),会花费CPU资源去处理!
如下图所示,R1发布一条路由(LSA),则R3会处理3份这条路由的copy:
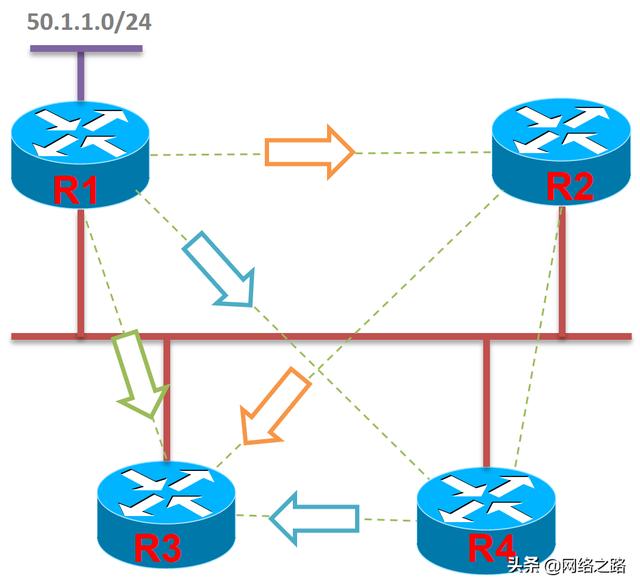
多份COPY
如果OSPF是以这种方式来交换路由信息,则随着网络规模的扩大,它就不能胜任了。OSPF中有专门针对这种情况的解决方案:选取DR/BDR。
DR/BDR减少邻接关系数量
选取DR/BDR是为了减少邻接关系数量的,它有如下的规则:
- BDR,DR Other都需要和DR形成邻接(adjacency)关系;
- DR Other需要和BDR形成邻接(adjacency)关系;
- DR Other之间不需要形成邻接(adjacency)关系,只需要形成neighbor关系;
邻居和邻接关系的区别,可以参见我之前的文章:OSPF中的邻居与邻接:一字之差,谬之千里;
鉴于上面的关系,存在一个公式来计算邻接关系的数量:邻接关系 = 2(n-1)-1,n代表路由器数量
则4个路由器,总共要形成5个邻接关系;5个路由器,会形成7个邻接关系;6个路由器,会形成9个邻接关系;
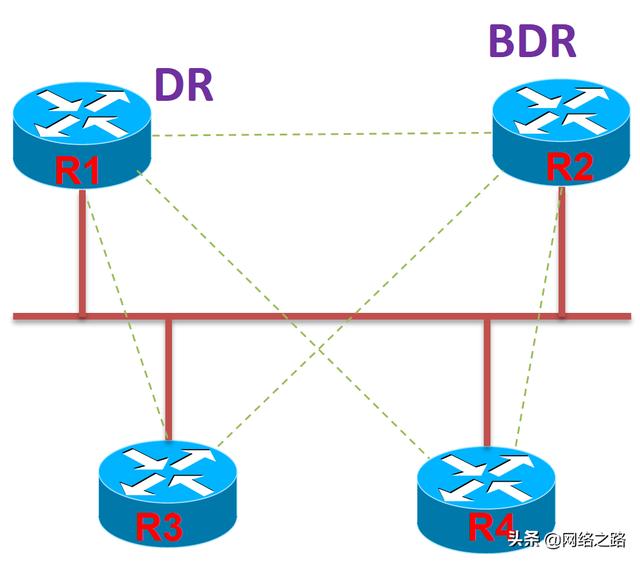
5个路由器,5个邻接关系
比没有DR/BDR时,邻接数量少很多,尤其是随着路由器数量的增长,差别更明显,可以参照下面的对比:
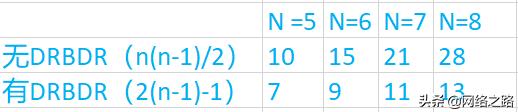
有无DR的邻接关系数量对比
总结
经过上面的描述,小伙伴应该对如何计算邻接关系了解了吧,其实我们只需要记住两个公式即可:
- 无DR/BDR时邻接关系数量 = n(n-1)/2,n代表路由器数量
- 有DR/BDR时邻接关系数量 = 2(n-1)-1,n代表路由器数量;
不过事物都有两面性,虽然在大规模OSPF网络中, 选取DR/BDR会节省很多的资源,不过在一个小网段上,例如只有两台OSPF路由器的网段,选取DR/BDR是浪费资源和时间的,路由器还要花费额外的资源去处理。