算法是数据科学不可分割的一部分。虽然很多数据科学家在学习的时候没有选修合适的算法课程,但它确实很重要。
比如说,许多公司在面试数据科学家时,都会问到数据结构和算法。
那么,现在问题是,问数据科学家这样的问题到底有什么用。
对于这个问题,我的答案是,数据结构问题可以被当作是对编码能力的测试。
我们都在人生的不同阶段接受过能力测试,但是这些测试并不能完美地评判一个人,几乎没有什么测试能做到这一点。
那么,为什么不用一个标准算法测试来评判一个人的编码能力呢?
因为算法和测试都并非死板,你总能在前者总结的基础上不断改进、创新,总能运用不同的算法来回应这些测试。
但这也并不意味着你可以不掌握基础就可以肆意动摇算法的地基。
牢固掌握基础算法的概念和运用,永远是一个优秀数据科学家必备的素质。
本文将以一种容易理解的方式帮助数据科学家快速回顾相关研究并介绍一些基本算法概念。
1. 递归/记忆化
递归是将定义的函数应用到自己的定义中。简而言之,递归是函数的自身调用。当你用谷歌搜索递归时,会遇到点小插曲。
刚开始学习数据科学的人可能会觉得递归有点难,但其实它很容易理解。一旦理解了,就会发现这是一个很棒的概念。
解释递归的最好例子就是计算一个数的阶乘。
def factorial(n):
if n==0:
return 1
return n*factorial(n-1)
- 1.
- 2.
- 3.
- 4.
可以很容易地看出阶乘是一个递归函数。
Factorial(n) = n*Factorial(n-1)
- 1.
那么如何将它转化为编程呢?
递归调用的函数通常由两部分组成:
- 基线条件——终止递归的条件。
- 递归公式——向基线条件发展的公式。
许多问题解决到最后,就是递归问题。这也适用于数据科学。
例如,一棵决策树是二叉树,树算法通常是递归的。或者,以我们经常使用的排序为例。排序的算法称为归并排序(mergesort),它本身就是一种递归算法。另一种是对分查找 (binary search),包括在数组中查找元素。
现在我们了解了递归的基本知识,接下来试着找到第n个斐波那契数。斐波那契数列是一系列数字,其中每个数字(斐波那契数)都是前面两个数字之和。最简单的数列是1、1、2、3、5、8等。要找到第n个斐波那契数,可以用如下代码:
def fib(n):
if n<=1:
return 1
return fib(n-1) + fib(n-2)
- 1.
- 2.
- 3.
- 4.
但是,发现问题了吗?
如果试图计算fib(n=7)要运行两次fib(5) ,运行三次 fib(4) ,运行5次 fib(3)。随着n越来越大,对同一数字进行了多次调用,递归函数对其进行了一次又一次的计算。
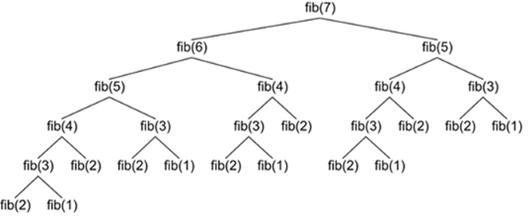
稍微改变我们的执行,添加一个词典来为这个方法添加一些存储。现在,每次计算出一个数字,这个备忘录词典就会更新。如果再出现同样的数字,就不需要再对它进行计算,而是可以直接从备忘录字典中得出结果。这种增加存储的方式被称为记忆化。
memo = {}def fib_memo(n): if n in memo: return memo[n] if n<=1: memo[n]=1 return 1 memo[n] = fib_memo(n-1) +fib_memo(n-2) return memo[n]
- 1.
通常,我会先写递归代码,如果它重复调用相同的参数,我会再添加一个词典来进行记忆化。
这帮助大吗?
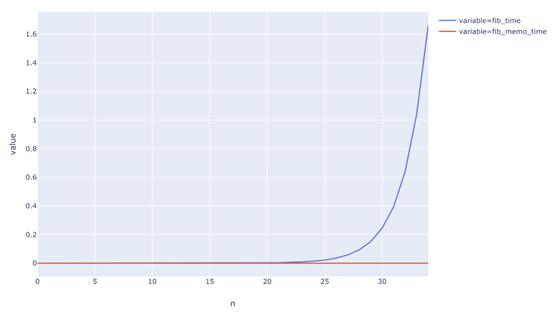
图中是不同n值的运行时间的比较。可以看到:没有记忆化的斐波那契函数运行时间呈指数性增长,而记忆化函数的运行时间则是线性的。
2. 动态规划
递归本质就是一种自上而下的方法。比如在计算斐波那契数n时,就是从n开始,然后对n-2和n-1进行递归调用,依此类推。
在动态规划中,我们采取自下而上的方法。这本质上是一种迭代编写递归的方法。首先计算fib(0)和fib(1),然后使用前面的结果生成新的结果。
def fib_dp(n):
dp_sols = {0:1,1:1}
for i in range(2,n+1):
dp_sols[i] = dp_sols[i-1] +dp_sols[i-2]
return dp_sols[n]
- 1.
- 2.
- 3.
- 4.
- 5.
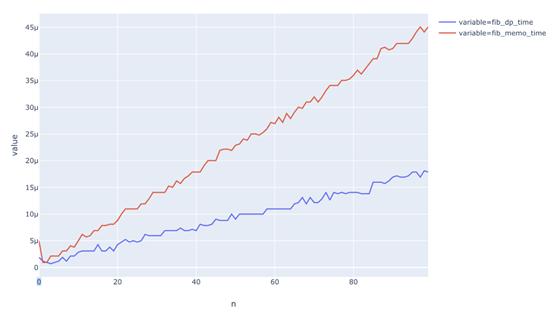
上图是“动态规划”和“记忆化”运行时间的比较。可以看出它们都是线性的,但动态规划更快一点。
为什么呢?因为在这种情况下,动态规划只对每个子问题进行一次调用。
关于开发动态规划的贝尔曼是如何选定“动态规划”这个名字的,有一个很有趣的故事:
“动态规划”这个名字是从哪里来的呢?20世纪50年代的数学研究情况并不是很好。当时,华盛顿有一位非常有趣的绅士,名叫威尔逊,他是国防部长。实际上,他对研究这个词怀有病态的恐惧和仇恨。那我能起个什么名字呢?首先,我考虑了“计划”、“决策”、“思考”。但是出于各种原因,“计划”并不是一个好词。于是,我决定使用“规划”一词。我想传递的概念是,这是动态的,多级的,并且是时变的。因此,我认为动态规划是个好名字,这可以一举两得。这是连国会议员都不会反对的。所以我决定采用这个名字。
3. 二进制搜索
假设有一个排序了的数字组合,要从这个数组中找出一个数字。我们可以采用线性搜索,挨个地检查每一个数字,直到找到特定数字。问题是,如果数组包含数百万个元素,这种方法就需要花费很长时间。这种情况下,可以采用二进制搜索方法。
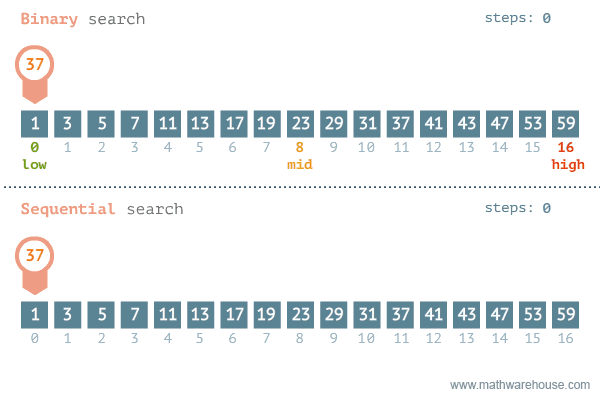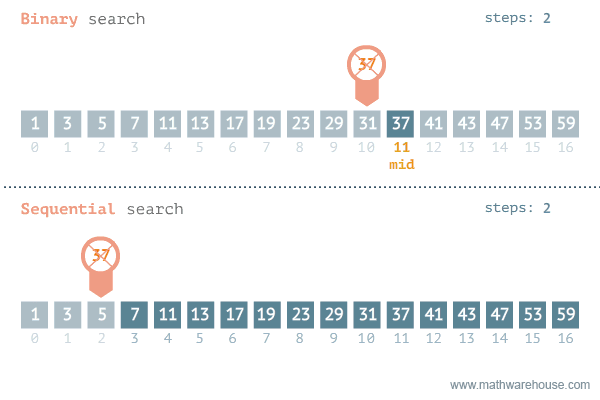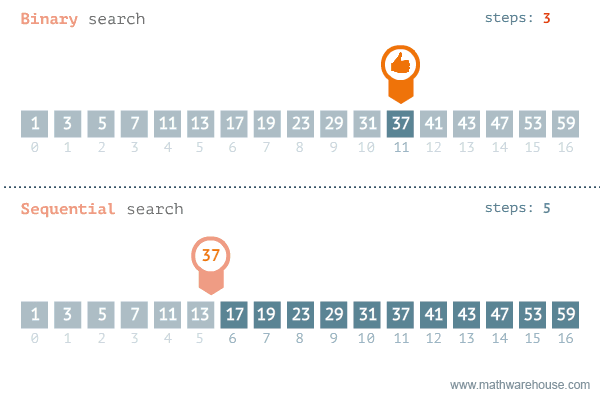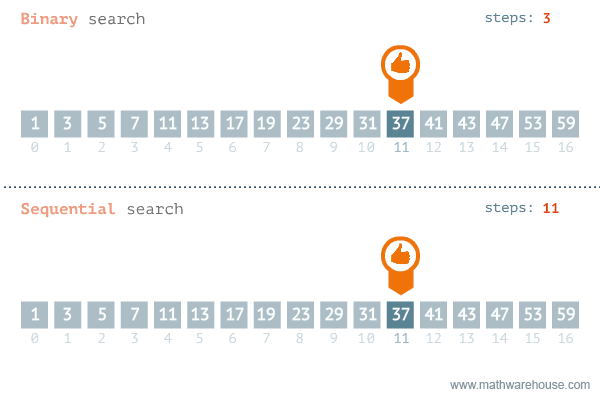
来源:发现37-海洋中有3.7万亿条鱼,他们正在寻找其中的1条
# Returns index of target innums array if present, else -1
def binary_search(nums, left, right, target):
# Base case
if right >= left:
mid = int((left + right)/2)
# If target is present at themid, return
if nums[mid] == target:
return mid
# Target is smaller than midsearch the elements in left
elif nums[mid] > target:
return binary_search(nums,left, mid-1, target)
# Target is larger than mid,search the elements in right
else:
return binary_search(nums,mid+1, right, target)
else:
# Target is not in nums
return -1nums =[1,2,3,4,5,6,7,8,9]
print(binary_search(nums, 0, len(nums)-1,7))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
这是一个基于递归算法的高级例子。利用数组被排序的事实,递归地查看中间元素,看看是想在中间元素的左边还是右边搜索。这使得每一步的搜索空间减少2倍。
因此,二进制搜索算法的运行时间是O(logn),而不是线性搜索的O(n)。
这有什么作用呢?下面是运行时间的比较。我们可以看到二进制搜索与线性搜索相比是相当快。
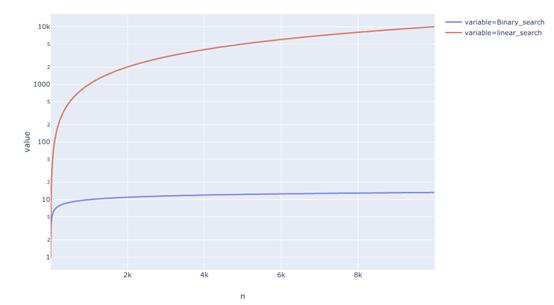
当n=10000时, 二进制搜索需要大约13步,线性搜索需要10000步。
结论
本文谈到了一些构成编程基础的算法,虽然是基础,但也同样令人兴奋。
数据科学家在面试时会经常被问到这些算法,深入理解它们可能会帮助你找到理想的工作哦。
尽管你不学习这些算法也可以在数据科学中取得进步,但你可以把学习它们当作一种乐趣,培养兴趣的同时还可以顺便提高编程技能。
一举两得,何乐而不为呢?