“概率是生命的向导。”——列纳德·蒙洛迪诺, 《醉汉的脚步:随机性如何支配我们的生活》
首先,确保你想戏弄的人真的聪明。
其次,提的问题需直观易懂。
事实上,在互联网领域,仍存争议的严谨话题所剩无几(因为有谷歌和维基百科)。
但今天笔者要讨论的是过去几年在互联网上引起激烈讨论的话题。科学专家和数据科学家在这一问题上各有看法。
事不宜迟,现在开始吧。
先来看问题
列纳德·蒙洛迪诺是一名物理学家,他与斯蒂芬·霍金合著了《宏伟设计》一书。他的著作《醉汉的脚步:随机性如何只陪我们的生活》还谈到了随机性,以及导致人们误解随机事件和随机过程的认知偏见。
在介绍“样本空间”概念的章节中,蒙洛迪诺使用了以下示例:
问题A:儿子还是女儿
我的朋友尼克有两个孩子,他告诉你他至少有一个女儿,那么另一个孩子是女孩的概率是多少? 这似乎是一个简单的问题,直接的回答是:已知其中一个是女孩,所以另一个孩子是女孩的几率应该是50%,对吗?
不对。
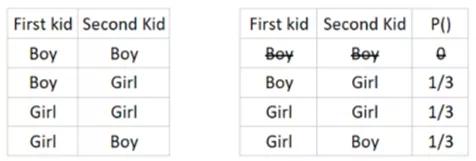
根据样本空间理论,可以如下列出所有可能的样本组合:
表中显示,答案是1/3,即,33.3%。
蒙洛迪诺指出,这个问题令人困惑的部分是题目内容,如果题中指定第一个孩子为女孩,那么第二个孩子为女孩的概率是50%。
辩论
然而,另一位有识之士不同意蒙洛迪诺的理论。 加里·史密斯(Gary Smith)是波莫纳学院(Pomona College)的经济学教授。他在耶鲁大学获得经济学博士学位,后被聘为助理教授。 他在《基本统计、回归和计量经济学》一书中引用了上述蒙洛迪诺采用的例子,认为这是对现实世界的典型误解,并从另一角度提出了问题。
问题B:另一个孩子
你看到我的朋友尼克和他的女儿在街上散步。尼克告诉你他家里还有一个孩子,那么,另一个孩子是女孩的概率有多大?
这个问题看起来和蒙洛迪诺提出的问题十分相似,但加里却给出了完全不同的答案与解析。
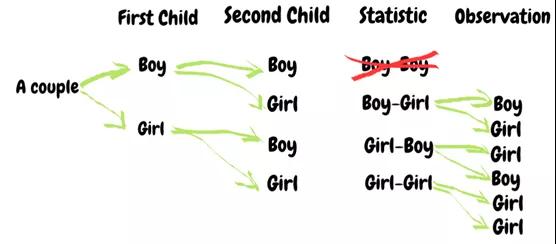
首先,他指出蒙洛迪诺“33.3%”的答案是错误的,然后他通过下表中的推算给出了自己的正确答案。
男孩用B表示,因此BB表示第一个孩子是男孩,同理,第二个孩子也是男孩。
女孩用G表示,BG表示第一个孩子是男孩,第二个是女孩。
该表显示了400个家庭平均分配了4种孩子类型,即,每种类型为100。根据加里所证,可以得出以下推论:
已知事实
- 在100例的BB中,尼克应该总是和男孩散步。
- 在100例的GG中,尼克应该总是和女孩散步。
- 如果尼克有儿有女,则合理的假设是,他和男孩或女孩一起散步的概率是相同的。
分析
- 观察表格的第一行。当尼克和一个女孩散步时,其中有100例(GG)表明另一位不在场的孩子也是女孩,而其他50+50例(BG&GB)则表明缺席的孩子是男孩。
- 当尼克和一个男孩散步时,也可以做出同样的推论,因此,比较BB与BG+GB(100 vs 50+50),也可以得出同样的结论
结论
不管现在和尼克散步的是男孩还是女孩,另一个孩子是“男孩或女孩”概率保持不变(它们是自变量)因此答案是1/2,而不是1/3。
当然,还有一个更为直观的解释:你看到一个女孩,这是一个独立的事件,对其他孩子的性别没有影响。
如果你现在还没有丝毫的困惑,那么你可能对这个问题还只停留在表面理解上(也可能你是个真正的天才,那便来看看下面的解释是否与你的思维过程相同)
深入探讨这个问题…
那么,加里和蒙洛迪诺,谁对谁错?
实际上,他们都是对的,因为他们试图解决的是两个不同的问题。再看看以上的问题。
- A:我的朋友尼克有两个孩子,他告诉你他至少有一个女儿,那么另一个孩子是女孩的概率是多少?
- B:你看到我的朋友尼克和他的女儿在街上散步。尼克告诉你他家里还有一个孩子,那么,另一个孩子是女孩的概率有多大?
两个问题有什么不同吗,“看见一个孩子是女孩”和“一个孩子是女孩”一样吗?
你认为呢?现在就是把聪明人弄糊涂的时候了。经济学教授加里混淆了以上两者的区别。
贝叶斯方程是解释这个问题最简单、最优雅的方法,尽管如此,笔者还是想从另一角度(使用全概率定律)来看待该问题。
“至少有一个女儿”和“看到一个女孩”不是一回事。这是关键。
这两个前提在时间和空间维度上的差异可以表示为“全局关系vs.局部关系”。
1. 空间维度上的“全球关系 VS 社会关系”
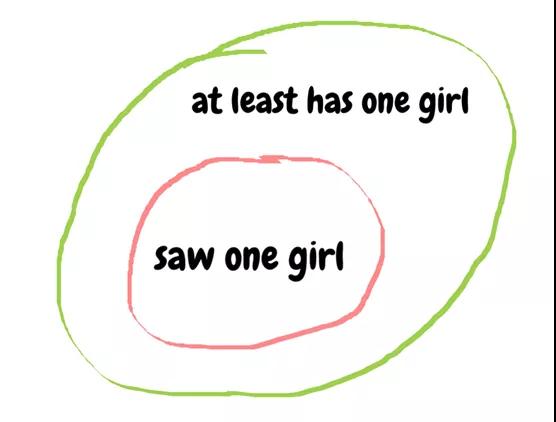
“至少有一个女儿”并不代表你能看到那个女孩
如上图所示,“至少有一个女儿”包含了“看到一个女孩”,而“看到一个女孩”所传递的信息更具概率描述。
2. 时间维度上的“全球关系 VS 本地关系”
“至少有一个女儿”是鸟瞰的统计结果角度。
“看见一个女孩”是人类观察的角度。
下面是更直观的描述,
统计是对样本空间的总体描述。观察是对平行空间中一种可能组合(所有可能发生的事情)的实际描述。 在理解了这两个问题之间的根本区别之后,可以得出结论:
- “至少有一个女儿”是样本空间中的一个概率问题。因此答案是1/3;
- “看见一个女孩”是根据目前的观察作出的未知推断,这是一个贝叶斯统计计算。
因此,“看到一个女孩,问另一个孩子是女孩的概率”就等于“有两个孩子,你看到其中一个是女孩,那么这个家庭有两个女儿的概率是多少?” “猜性别”的话题到此结束。 笔者想总结的是,即使是系统1(快速直观的本能,以及由‘或快或慢思考’产生的情感大脑)也没有很好的概率直觉。但是,我们总是可以通过增强对概率因果关系的认识,来提高自己解释周围环境中的动态和不确定性的能力。
总结
如何通过概率建立主观假设与客观结果之间的联系?
为什么对真实世界的观察会影响事件的偶然性概率? 将要发生的事情和已经发生的事情有什么根本的区别?
最后,如想找到一种回答这些问题的方法,或者想戏弄你的智能数据科学家朋友,可阅读以下书籍:
- The Drunkard’s Walk: How Randomness Rules Our Lives
- EssentialStatistics, Regression, and Econometrics
- The Book of Why: The New Science of Cause and Effect