本文用matlab程序,模拟微信给10个人发红包,设定次数1亿次,统计每个人抢到的红包,最佳手气和最差手气次数,用以分析红包是应该先抢还是后抢?
算法解释
网上有人分析微信红包用的方法是两倍均值法,意思即:每个人抢的额度为0.01到总额度除以剩余人数的两倍。本文用此方法来判断,
- 假定有10个红包共100元,此时均值为10,第一个人(设定为P1)抢到的值为0.01-20元内任意值。设P1抢到12元;
- 此时还剩下9个红包共88元,此时均值为9.77,第二个人P2抢到的值为0.01-19.55元内任意值。设P2抢到3元;
- 此时还剩下8个红包共85元,此时均值为10.625,第三个人P3抢到的值为0.01-21.25元内任意值。
- 依次计算下去,到第9个人抢完后,剩下钱的全是最后一个人的。
代码实现
本次计算,设定每次发10个红包,共100元。首先生成三个矩阵用以存放红包值、手气最佳次数、手气最差次数。redluckymoney是我能想到红包较好的翻译了
- redluckymoney=zeros(100000000,10);%存放每次抢到的红包值
- bestlucky=zeros(1,10);%统计每个人手气最佳次数
- worstlucky=zeros(1,10);%统计每个人手气最差次数
再进行计算,先进行内循环,发10个红包,统计手气最佳和手气最差,再进行外循环100000000次。
- for n=1:100000000
- for i =1:9
- redluckymoney(n,i)=rand(1)*((100-sum(redluckymoney(n,:)))/(11-i)*2);
- end
- redluckymoney(n,10)=100-sum(redluckymoney(n,:));
- [~,maxtemp]=max(redluckymoney(n,:)); %计算手气最佳次数
- bestlucky(1,maxtemp)=bestlucky(1,maxtemp)+1;
- [~,mintemp]=min(redluckymoney(n,:)); %计算手气最差次数
- worstlucky(1,mintemp)=worstlucky(1,mintemp)+1;
- end
最后是画图,单次抢到的钱数,如果你的电脑牛X的话,可以放到外循环中,展示动态。但计算速度会大大降低,1亿次计算时间会很长long long long……
- bar(redluckymoney(n,:),'FaceColor',[0.8 0.1 0],'EdgeColor',[1 1 0],'LineWidth',1.5);
- ylabel('单次抢到红包/元','fontsize',14,'color','b','fontweight','bold');xlabel('参与人','fontsize',14,'color','b','fontweight','bold');
- title('单次红包钱数','fontsize',16,'color','b','fontweight','bold');
- bar(sum(redluckymoney_sum),'FaceColor',[0.8 0.1 0],'EdgeColor',[1 1 0],'LineWidth',1.5);
- ylabel('总共抢到红包/元','fontsize',14,'color','b','fontweight','bold');xlabel('参与人','fontsize',14,'color','b','fontweight','bold');
- title('总红包钱数','fontsize',16,'color','b','fontweight','bold');
- bar(bestlucky,'FaceColor',[1 1 0],'EdgeColor',[1 0 0],'LineWidth',1.5);
- ylabel('手气最佳/次','fontsize',14,'color','b','fontweight','bold');xlabel('参与人','fontsize',14,'color','b','fontweight','bold');
- title('手气最佳次数','fontsize',16,'color','b','fontweight','bold');
- bar(worstlucky,'FaceColor',[0.5 0.5 0.5],'EdgeColor',[0 0 0],'LineWidth',1.5);
- ylabel('手气最差/次','fontsize',14,'color','b','fontweight','bold');xlabel('参与人','fontsize',14,'color','b','fontweight','bold');
- title('手气最差次数','fontsize',16,'color','b','fontweight','bold');
统计出来,每个人总抢到的钱数如下图,总钱数基本一致,意味着无论先抢到,还是后抢到,经过多次后,抢到的钱是一样的。
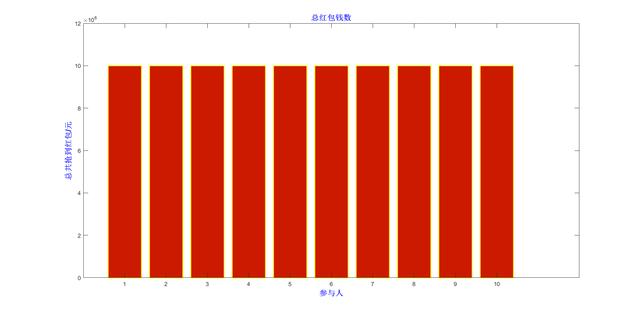
总抢到的钱数
手气最佳和手气最差如下图:总体来看,最后抢的两位容易获得手气最佳,也容易获得手气最次差,更有可能是啥也抢不到……
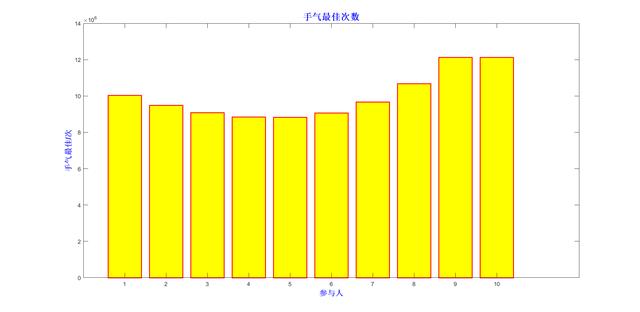
手气最佳次数
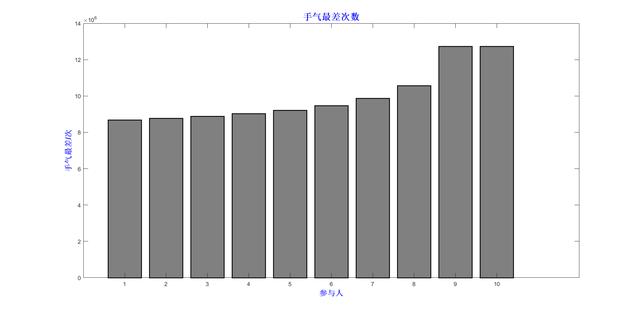
手气最差次数
总结
- 无论先抢还是后抢,经过多次抢红包后,总金额是一致的,为了防止抢不到,建议还是先抢吧。
- 最后面两个人有最高概率成为手气最佳或手气最差。在能保证抢到红包的前提下,后抢有机率成为手气最佳。