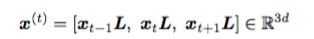本文经AI新媒体量子位(公众号ID:QbitAI)授权转载,转载请联系出处。
“不要回答!不要回答!不要回答!”
刘慈欣在为自己的科幻小说起名为《三体》时,他早已知道“三体”本身就是一个不可回答的问题。

“三体问题”已经困扰了人类几百年,曾经无数让你感到恐惧的大牛都为此付出了巨大的心血,比如牛顿、欧拉、拉格朗日、庞加莱,直到今天还有很多人在研究。
但遇事不决,用神经网络总是没错的。
最近来自爱丁堡大学、剑桥大学的数学家们,用神经网络来求解三体问题,速度比之前的求解器快一亿倍,而且误差只有十万分之一。
“我太难了”
那么三体问题到底是什么,为什么它会难倒如此多的物理学家、数学家?
N体问题是指,根据牛顿三大运动定律和牛顿万有引力定律,在知道N个质点的初始位置和速度的情况下,求解其后续运动的问题。
首先,二体问题极易解决,人类早已掌握地球围绕太阳运转的规律,开普勒行星运动三大定律就是答案。
所以在牛顿提出了万有引力后,一开始人们以为,三体问题不过是比二体问题多一体,也没什么难的嘛,就是多加一个方程而已。
然而事情并不简单,当物体增加到3个以后,一般来说,运动轨迹就会变成乱七八糟的曲线,不再像椭圆那样优美简单。
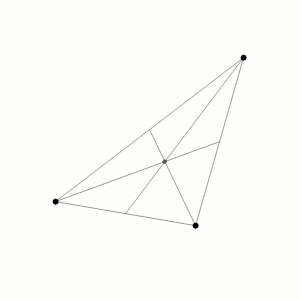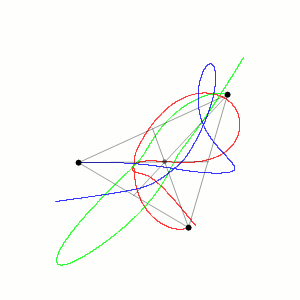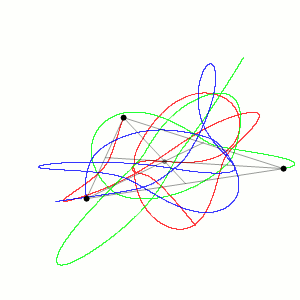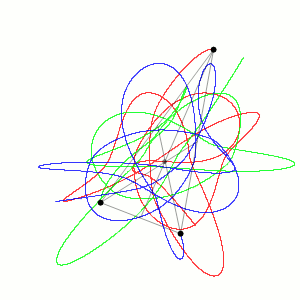
虽然三体问题虽然只包含三个方程,但数学上已经证明,除了少数特殊情况,一般是无法找到解析解的,我们只能用数值模拟的方法求得近似解。
在欧拉、拉格朗日等大牛的努力下,数学家找到了一些特殊三体问题的精确解,比如三个等质量物体绕“8”字运动。
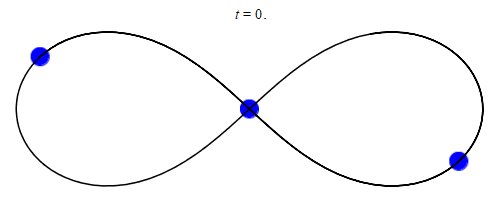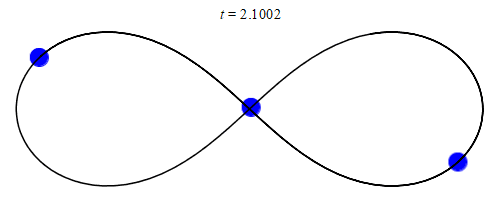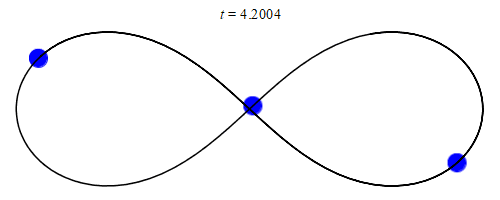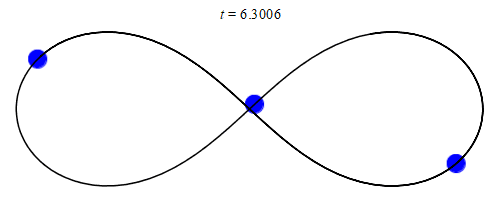
但是大多数三体问题还是无法求出精确解的,而且就像混沌里的蝴蝶效应一样,只要初始条件有一些细微的差异,就会导致结果大为不同。
为此需要有巨大算力的计算机去求解三体问题。由于系统的混沌性质,只能通过费时费力的迭代计算来找到给定初始化问题的解。
2015年,有人开发了开发了Brutus积分器,可以按任意精度计算出求出任意N体问题的近似收敛解。
但是,迭代计算随着精度的不断提高和模拟时间的增长,需要在内存中保留的数字精度呈指数级增长,并且计算的步长要进一步缩小。
神经网络可不是瞎蒙
既然用传统的数值解法难度很大,不妨试一试神经网络。
不过最近神经网络的跨界比较多,有人用来预测余震,有人用来诊断心脏病,最后发现都不靠谱。
物理学家、数学家在使用深度神经网络之前,当然不能随便硬套,得先证明这不是玄学。
早在1991年,已经有人用理论证明,如果神经网络的激活函数是连续、有界且非恒定值的,则可以在紧凑的输入集上实现连续映射。
说得通俗些,一个包含足够光滑激活函数的网络,能够以任意精确度逼近函数及其导数。也就是说,用神经网络可以找到三位问题中物体运动方程的近似解。
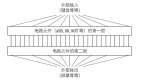
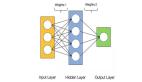
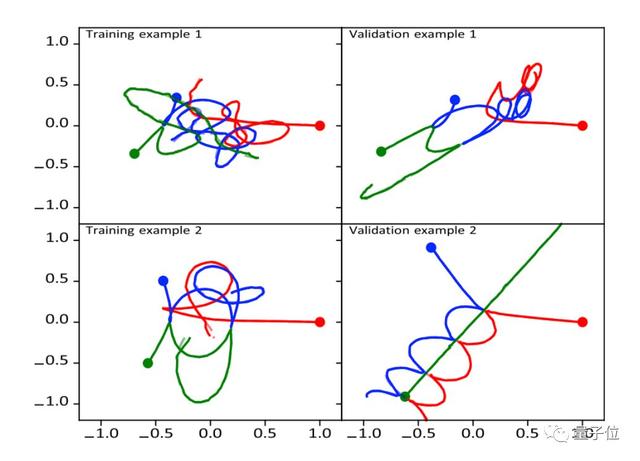
作者使用了由128个节点、10个隐藏层组成的前馈神经网络。使用ADAM优化算法对数据进行训练,其中每个epoch分为5000个batch,并将激活函数设置为ReLU。
训练集和验证集分别由9900和100个模拟数据组成。在每个模拟中,通过Brutus积分运动方程求解,与神经网络的结果进行对照。
通过输入时间t和粒子的位置坐标,以上的神经网络返回其他粒子在该时刻的坐标,从而实现了近似求解三体问题。
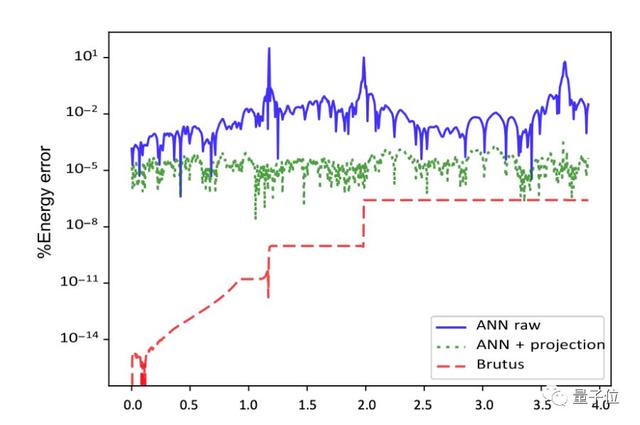
在这个过程中,神经网络需要的时间平均比Brutus积分器快10万倍,最高可以快一亿倍。
不过,还有是该方法还是遭到了一些网友的质疑,原因是它只解决了在二维平面内的三体问题,粒子的初速度也限制为0。
而且神经网络在求解问题的时候似乎没有遵循能量守恒定律,最后靠作者引入了一个“能量投影层”,才实现了误差10-5的结果。
但是这种方法为我们快速低成本计算航天器轨道提供了一种解决思路。
论文地址:
https://arxiv.org/abs/1910.07291