当年我还是个学生的时候,有一次去参加欢聚时代的一个面试,有一道面试题记忆尤新,让你来实现一个定时任务,你会怎么做?为了简化问题,我们只用考虑内存方案,不用考虑数据持久化。
数组法
最简单的,我们可以把所有的任务存放在一个数组里面,然后,每隔单位时间遍历整个数组,找到是否有任务满足当前时间,如果有,那么从数组中取出,然后执行。每隔单位时间查询算法复杂度为O(N)。
那么,新增一个任务怎么操作呢?我们只要简单地往数组中追加一个元素即可,算法时间复杂度为O(1)
优先队列法
评估一个算法,我们既要考虑它的查询算法复杂度,也要考虑他的插入算法复杂度。在定时任务场景中,很显然,查询场景是非常多的。几乎我们每个单位时间都要轮询一遍,那么我们有没有优化算法的可能呢?
我们每次查询,都只要查询时间最接近当前时间的,时间比当前时间更早的,肯定被我们丢弃了。所以这个题目,等价于我们查询队列里面时间最小的。我们不禁想到一个熟悉的数据结构,优先队列!活着我们可以使用一个小根堆进行实现。
每次我们插入一个新的定时任务,我们将一个任务插入优先队列,每次插入的时候,队列内部需要进行调整,算法时间复杂度为O(logN)。值得注意的是,在讨论算法时间复杂度的时候,logN是Base2的,也就是说,如果N等于8的时候,logN就是3。
同理,虽然我们可以在O(1)的时间里面找到时间最小的任务,但是如果我们取出这个元素,优先队列需要做内部的调整,这个算法时间复杂度也是O(logN)的。
时间轮法
上述优先队列的算法,综合算法时间复杂度是O(logN)的,已经很高效了,但是在我们大并发的分布式系统下,这个速度,还是太慢了。我们有没有更高效的算法呢?
那便是时间轮算法,时间轮是一个环形队列,按照时间的单位区分,我们假设1秒,每个单位里面,是一个链表,用来存储定时任务。
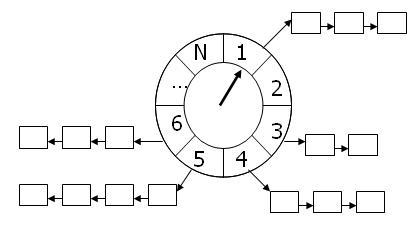
可能你会问,一个环形队列里面的元素,毕竟是优先的,如果超过了长度,我们该怎么办呢?我们可以联想到我们家里的水表,是不是也有很多个轮子,每一个轮子的单位不一样!
同样,时间轮也是如此,我们可以用多级时间轮进行优化,就跟我们的时钟或者水表一样,这一层的走了一圈,下一层的才走了一格。
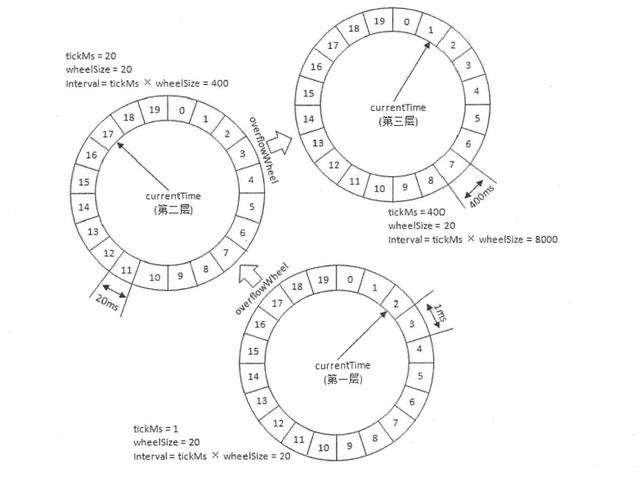
那么,这个算法的 时间复杂度怎么计算呢?插入的时候,我们从低层开始查找,找到在哪一层,然后直接插入对应的刻度。假如我们的时间轮有5层,那么我们最多查找5次。
查询的时候,我们每一秒都是推动时间轮的滚动,每次都是直接取队首的元素,相当于算法时间复杂度为O(1)。当转了一圈的时候,把下一层的下一格再推下来。这样子,我们一个元素,最多会从第5层,逐渐插到第1层,综合下来一个元素最多会被插入5次,在算法时间复杂度评估的时候,我们通常会忽略常数,最终算法时间复杂度为O(1)。
总结
一个非常简单的面试题,竟然有好几种不同的解法。这才是算法与数据结构的魅力,欢迎大家关注我,共同学习,共同进步。大家的支持是我继续唠嗑的动力。































