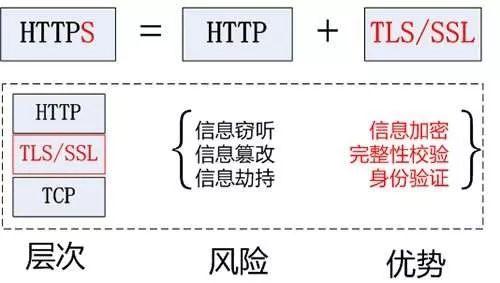
本篇文章介绍一下程序员都应该了解的网络通信相关的安全基础知识。下面,我们一起来看。
通信风险
- 窃听风险(eavesdropping):第三方可以获知通信内容。
- 篡改风险(tampering):第三方可以修改通信内容。
- 冒充风险(pretending):第三方可以冒充他人身份参与通信。
风险防范
- 信息加密传输,第三方无法窃听。
- 增加校验机制,一旦被篡改,通信双方会立刻发现。
- 配备身份证书,防止身份被冒充。
哈希(Hash)
哈希也叫散列,是把任意长度的输入通过散列算法变换成固定长度的输出,该输出就是散列值,也叫摘要(Digest)。
哈希是一种压缩映射,通常不可逆
这种转换是一种压缩映射。也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,所以不可能从散列值来确定唯一的输入值,但如果输出的位数足够,不同输入散列成相同输出的概率非常非常小。
简单的说,散列就是一种将任意长度的消息压缩到某一固定长度的消息摘要的过程。
散列是不可逆的,也就是无法通过输出还原输入,此特性常被用于密码保存。
SHA-512、MD5等都是著名的散列函数,MD5生成的散列码是128位,甚至MD5就是哈希的同名词,你可以通过网站:https://passwordsgenerator.net/sha512-hash-generator/ 在线计算哈希。
散列有什么用?
- 散列可用于保存密码,明文保存密码是危险的。通常我们把密码哈希加密之后保存,这样即使泄漏了密码,因为是散列后的值,也没有办法推导出密码明文(字典攻击难以破解)。验证的时候,只需要对密码(明文)做同样的散列,对比散列后的输出和保存的密码散列值,就可以验证同一性。
- 可用于验证下载文件的完整性以及防篡改,比如网站提供安装包的时候,通常也同时提供md5值,这样用户下载之后,可以重算安装包的md5值,如果一致,则证明下载到本地的安装包跟网站提供的安装包是一致的,网络传输过程中没有出错。
加密
加密就是把明文变成密文的过程,解密就是反方向把密文变成明文。
比如著名的凯撒密码,就是把每个字对应到另一个,这样的话,只要有密码本,就能对照完成加解密。比如最简单的,对于英文26个字母,每个字母右移3个,abc变成def,这也是一种加密,当然这种加密很简单,很容易被破译。
而诸如AES(高级加密标准)、3DES(三重数据加密算法)则被公认为很难破解,不过山东大学女教授王小云很厉害,破解了MD5和SHA-1,迫使加密标准升级,最终当上了院士。
1. 对称加密
对称加密就是加解密的密钥是一样的,优点是快,这也是传统的加密方式,像AES、3DES都是对称加密。
2. 非对称加密
非对称加密用于加解密的密钥不一样,有2个密钥,公钥和私钥,公钥可以公开,私钥妥善保管。RSA、ECC(椭圆曲线加密算法)、DH(密钥交换算法)这些都是非对称加密。
非对称加密很慢,有多慢?相比对称加密慢1000倍,因为慢,所以它常用于密钥协商(Handshake),协商出会话密钥后,再用对称密钥加密通信数据。
1976年,Whitfield Diffie和Martin Hellman首次提出了非对称加密的概念,该算法被称为Diffie-Hellman密钥交换。然后在1978年,麻省理工学院的Ron Rivest,Adi Shamir和Leonard Adleman发表了RSA 算法。这些都可以被视为非对称加密的基础。
非对称加密也称为公钥基础结构,又称PKI。非对称加密的提出是密码学上的一次革命,影响深远。
非对称加密算法用私钥加密,用公钥解密,或者用公钥加密,用私钥解密。
证书
证书就是为了证明我是我,比如你要访问中国银行网站,但中行官网如何证明它是中行官网呢?答案就是数字证书。
CA是数字证书中心,服务器需要找CA做认证,让CA给自己颁布数字证书,数字证书内一般包含服务的一些信息、以及服务器的公钥,通过CA的私钥加密后,产生的数字证书,因为CA的权威性,且它的公钥天下皆知,所以,如果你能用CA的公钥解开证书,那便可证明该证书一定是CA颁发的,要不然它不会有CA的私钥,也便没法产生可用CA公钥解密的证书。
所以,由此可见,数字证书用到了非对称加密。
数字签名
日常生活中也有签名,每个人的笔迹是不一样的,你刷卡消费后在账单签上大名,服务员校验过之后保存下来,你哪天赖账,便可以有签名为证,因为别人写的字跟你的笔迹终有差别。
那数字签名是什么呢?比如a发一封email,接收方怎么证明这封信是a写的?
本质上,数字签名也是利用了非对称加密。
前面讲了,非对称加密有公钥和私钥,如果发生方用私钥加密,然后接收方用发送方的公钥可以解密,那便可以证明是从某发送方发送的,因为别人拿不到你的私钥,也便无法用你的私钥加密,你不能抵赖。
数字签名通常先对内容算哈希,产生内容摘要,再用私钥加密,得到签名。
密钥协商
下面举一个例子来说明这几个问题:
张三有2把钥匙,一把公钥,公告天下,一把私钥,妥善保管,只有自己知道,很明显,非对称加密。
李四给张三写信,写完之后,用张三的公钥加密,通过邮局寄给张三,即使邮递员拆开信封看,他也看不懂,因为内容是密文,只有张三的密钥才能解密。
张三收到信后,用私钥解密,可以正常阅读。
现在张三要给李四回信,写完后,用hash函数生成摘要digest。
然后张三,再用私钥对摘要加密,生成数字签名signature。
然后把签名附在信的下面,一起发给李四。
过程是:信明文 -> hash -> digist -> 私钥加密 -> signature。
李四收到回信后,用张三的公钥对数字签名解密,得到摘要,由此证明,信确实是张三发出的,为什么?因为如果不是张三发的,那写信的人就没有张三私钥,用别的私钥加密得到的签名,是无法用张三的公钥解开的。
李四,再对信的内容做hash,得到摘要,与上一步得到的摘要对比,如果一致,则证明信的内容没有被修改过,信的内容是完整的。
复杂的情况出现了。
王五,用自己的公钥替换李四保存的张三的公钥,也就是王五欺骗了李四,李四误把王五的公钥当张三的公钥,这样一来,王五就能冒充张三给李四写信(王五用自己的私钥加密)。
问题是什么?问题是李四不能确信自己保存的公钥真的是张三的公钥。如果客户端电脑上存的工商银行官网的公钥,实际上是骗子公司的公钥,那就麻烦大了。
怎么破?让张三去认证中心CA(Certificate Authority),为公钥做认证,怎么做呢?CA中心用自己的私钥,对张三的公钥和其他相关信息一起加密,生成数字证书(Digital Certificate)。
张三拿到数字证书后,以后给李四回信,在签名的同时,附带上数字证书。
李四收到信之后,从CA的公钥解开数字证书,取出张三的公钥(一定是真的),然后就能放心的愉快的按之前的流程解开签名了。
数字证书加入后,核心区别就是张三的公钥不再保存在李四处,而是通过数字证书下发。
为什么数字证书里的张三的公钥一定是真的呢?因为CA是权威机构,假设全世界就一家(其实不止,但也不多),它的公钥天下尽知,就是固定的串,所以能用CA公钥解开的证书,一定是CA颁布的,因为CA用它的私钥加密产生的证书。很明显,非对称加密能用于证明我是我。
密钥交换算法
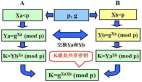
著名的DH密钥交换算法,这个算法很有意思,也很巧妙,简而言之,就是通信双方交换一点信息(不怕被偷看到),然后就在两端,分布产生出一个相同的密钥,神奇啊。
有一个很有意思的例子。
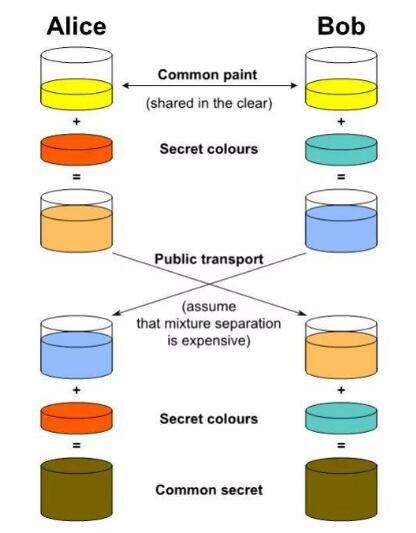
Alice和Bob要协商出一个公共的颜色,他们可以交换信息,但交换的信息,可以被偷看到,怎么办?既能协商出公共颜色,又不能让别人知道呢。
- 首先,他们有公共的颜色,都是1毫升黄色。
- 然后Alice挑选一个私密的红色,Bob选绿色,都是1毫升。只有自己知道,不会告诉别人。
- 然后Alice把黄色和红色混合在一起,Bob把黄色和绿色混合在一起,各为2毫升。
- 然后,他们把自己混合后的2毫升颜色液体,发给对方。
- 然后,用自己的一毫升私密颜色液体,跟从对方那里收到的2毫升液体,混合,下面就是见证奇迹的颜色的时刻,他们得到了相同的颜色,而第三方并不能通过偷看他们传递的数据知道他们最终得到的颜色(基于一个假设,图里有说明)。
密钥交换算法的原理跟这个差不多,网上有大量的资料讲述这个问题,我觉得理解了上面的例子,再看ECDH便也不难了。
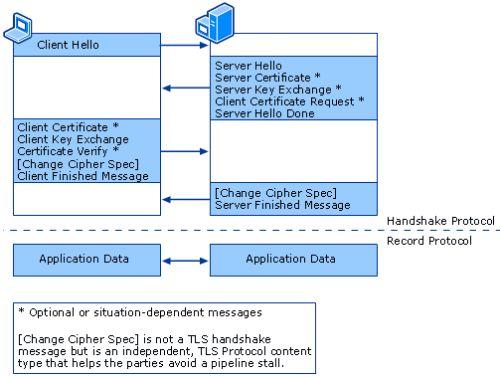
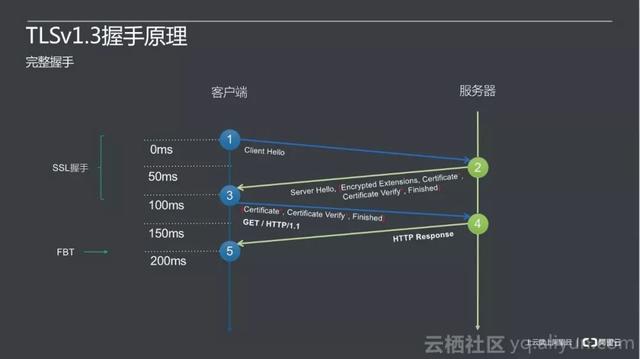
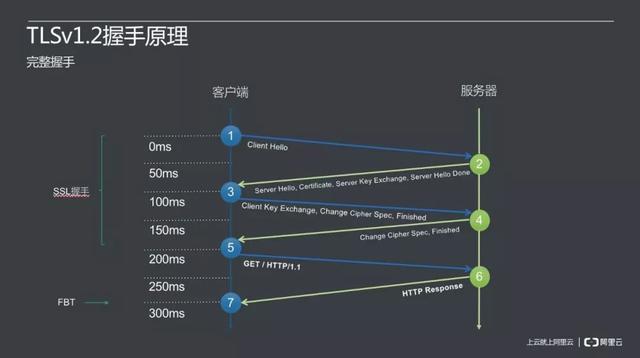
众所周知http是互联网协议,但是它不够安全,所以后面有改进版的https,其实就是多了一个TLS,这个是传输层加密,本质上,就是通过handshake,协商出一个会话密钥,后面的数据传递,都用这个密钥做对称加解密。
我们经常讲安全通道,其实也就是协商出一个会话密钥,他并不神秘。胡乱放几张图片吧。
为了减少这几个RTT,又想了各种办法,然后复用连接的话,就可以做到0RTT,1RTT了。
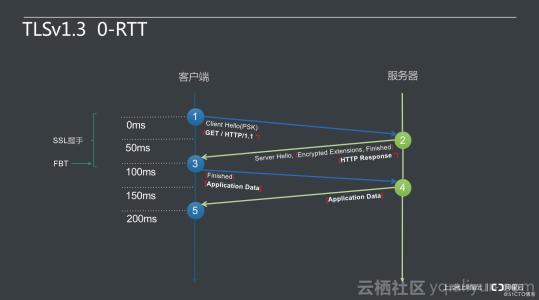
就说这些吧,最后抛几个名词,有兴趣自行百度学习:DTLS,HMAC,AEAD,重放攻击,放大攻击,是不是很高端?